|
|
GIZE, STONEHENGE, CHICHEN ITZA, ETC,ETC: EL MISTERIO DE LAS PIRAMIDES Y LA ESFINGE DE GIZEH
Elegir otro panel de mensajes |
|
|
1ª PARTE
LA TECNOLOGÍA IMPOSIBLE
Me considero un buscador del pasado de la humanidad y un investigador que se busca a sí mismo. Un buscador de la verdad y de una historia que nos han robado y ocultado, adoctrinado y moldeado como a <> para que la repitamos de memoria. Pero la Humanidad está despertando, gracias a que cada día estamos más conectados a una Gran Consciencia Universal y a Internet, por supuesto, el flujo de Luz, Sabiduría y Fraternidad Humana nos une cada vez más. Pero ese <> siempre desde la visión de Unidad en la Diversidad, Libertad, Respeto, Fraternidad, Generosidad y Amor Incondicional. Nunca desde un Sistema de Control y de Poder económico y religioso que trata de esclavizarnos y obligarnos a seguir unos oscuros planes de un Nuevo Orden Mundial. Nos negamos totalmente a esta fórmula venenosa. Ya nos han enseñado el Mundo que NO queremos. Ahora la Humanidad quiere dirigirse hacia un Nuevo Mundo. Un Mundo basado en el Lenguaje del Cosmos y la Naturaleza, en el respeto y cuidado de la Madre Tierra y todos sus seres, en la armonía material y espiritual. Y para ello se hace necesario descubrir nuestro pasado para entender nuestro presente, para corregir errores y recoger lo mejor que ha crecido en cada Civilización. Y un futuro que está lleno de posibilidades maravillosas para el florecimiento de una Nueva Humanidad.
Para esta serie de artículos, que no son sino una síntesis de muchas fuentes, vamos a utilizar la obra de varios autores visionarios, como Javier Sierra (En busca de la Edad de Oro), Robert Bauval y Graham Hancock (Los Guardianes del Génesis), Fernando Malkun (Documentales El Ojo de Horus y La Conexión Altlante), Patrick Gerlyn (La profecía de Orión), Albert Slosman (El Libro Egipcio de los Muertos, El Gran Cataclismo), John Anthony West (Serpent in the Sky), R. Swchaller de Lubicz (El Templo del Hombre), Enrique de Vicente (Año Cero), Drunvalo Melchizedek (El antiguo secreto de la Flor de la Vida), Elisabeth Haich (Initiation), Christian Jack (El saber mágico de Egipto), El Gran Hermes Trimegistos o Toth (El kybalion), Barbara Hand Clow (Cosmología Pleyadiana), Max Toth y Greg Nielsen (El Poder mágico de las Pirámides), Steve Alten (El Testamento Maya). y muchos otros investigadores que han aportado tanta ilusión, tiempo y esfuerzo en la búsqueda de la verdad. Podéis sentiros orgullos, no habéis predicado en un desierto. Vuestra investigación ha sido muy valiosa. A todos ellos gracias por dedicar vuestra vida y búsqueda de la verdad de los orígenes de la Civilización Humana. Y gracias sobretodo a La Creación y al Gran Arquitécto Cósmico, El Gran Músico de esta Sinfonía del Cosmos. Por último una Declaración Universal como seres humanos evolucionados: “El espacio no gira en torno a los logros tecnológicos y al ego individual, sino alrededor del Espíritu Divino y nuestra contribución al propósito Universal”.
En esta 1ª parte estudiaremos los detalles más técnicos y estructurales, basándonos en un punto de vista más científico, desvelando interesantes logros en el campo de la arquitectura e ingeniería, geometría y astronomía, dejando la faceta más intuitiva y esotérica para una 2ª parte, donde hablaremos del Kybalion, la Flor de la Vida, astrología egipcia y energía del punto cero aplicadas en la Pirámide de Gizeh.
“Cuando un ser humano cree que lo sabe todo deja de aprender”.

Fig 1. La Vía Láctea
Una galaxia en espiral, una de los 100.000 millones de galaxias de estrellas que se desplazan por el éter del espacio, cuya edad es de 5.000 millones de años, rotando como una rueda cósmica. Esta galaxia arrastra en su interior un gigantesco torbellino con más de 200.000 millones de estrellas y un número incalculable de astros.
Y en la Tierra hace 12.000 años, apenas un segundo del Tiempo Cósmico, se desarrolló una Civilización Antigua y Sabia en el país de Khemet (así se llamaba Egipto en la antigüedad), el legado de una herencia de una Civilización Milenaria que desapareció de la faz de la Tierra y que fue conocida como AHA-MEN-PTAH o La Atlántida.
SUS OBRAS EN PIEDRA SON SU LEGADO MONUMENTAL. Y su exposición mas grande y majestuosa fueron las Pirámides y la Esfinge de Gizeh.

Fig 2. Pirámides de Gizeh

Fig 3. Esfinge de Gizeh
Una Civilización que en los períodos iniciales tiene un mayor florecimiento y desarrollo y que pudiera no ser el producto de una generación espontánea, sino el final de una Antigua Civilización avanzada.
La Tecnología del Antiguo Egipto muestra más signos de retroceso que de progreso. Sabemos que las pirámides de los últimos faraones del Imperio Antiguo son notablemente inferiores, en términos de calidad y perfección técnica de la obra, en comparación a las grandes realizaciones de los antepasados. Este conjunto de pruebas demuestra una involución con el paso de las dinastías.
Nosotros creemos firmemente que las pirámides de Gizeh no se construyeron como tumbas, de hecho carecen de todo jeroglífico de identificación, de inscripciones internas, sarcófagos y tesoros de los que se pueda hablar. Los egiptólogos han querido hacernos creer que los faraones Keops, Kefren y Micerino fueron los que encargaron su construcción, pero las pirámides estaban allí mucho antes de que ellos nacieran.
Dicha falacia se remonta a 1837, cuando el coronel Howard Vyse recibió el encargo de excavar Gizeh. Este arqueólogo, no habiendo hecho ningún descubrimiento significativo, se las arregló, muy convenientemente, para descubrir unas marcas en la piedra que llevaban el nombre de Keops, en un túnel más bien poco claro que él mismo excavó al azar en el interior de la pirámide. Los egiptólogos pregonaron el descubrimiento de Vyse.
Muchos años después, el arqueólogo francés Auguste Mariette desenterró una estela inventario. El texto que apareció en dicha piedra, indica claramente que las pirámides fueron construidas mucho antes del reinado de Keops, y se refiere a las estructuras de Gizeh como la Casa de Osiris, señor de Rostau.
Fue a finales del siglo XIX cuando llegó a Egipto el ingeniero e investigador Flanders Petrie con un sofisticado equipo de medición que incluía niveles ópticos, calibres métricos, goómetros adaptados a ángulos, catetómetros,etc…Sus mediciones, las más exactas realizadas hasta ahora, han conseguido que puedan sacarse unas conclusiones que puedan ceñirse al rigor científico.
http://conscienciadespierta.wordpress.com/2010/12/20/el-misterio-de-la-piramide-y-la-esfinge-de-guizeh/ |
|
|
|
|
LA POSICION DEL SOL EN LA VIA LACTEA, EN EL CONTEXTO AL RIO NILO, ESTA DISEÑADA EN FUNCION A LA SEÑAL DE JONAS (ARCA PERDIDA/INDIANA JONES)
Here is an interesting read on Stargates and 19.47
In terms of Richard Hoagland's ' hyperdimensional physics' derived from the geometric 'message' of Cydonia (Mars), the conduit or 'stargate' between this world 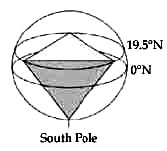 and the Otherworld (i.e. hyperspace) is prominently represented by the angle 19.5°. According to the theory, it is the tetrahedral geometry signified by this angle that enables inter-dimensional energy transfer between the two realms. and the Otherworld (i.e. hyperspace) is prominently represented by the angle 19.5°. According to the theory, it is the tetrahedral geometry signified by this angle that enables inter-dimensional energy transfer between the two realms.
 This 'stargate' geometry is expressed by a circumscribed tetrahedron (made up of four equilateral triangles). Interestingly enough, the hieroglyphic sign denoting Sirius was a triangle in ancient Egypt. This 'stargate' geometry is expressed by a circumscribed tetrahedron (made up of four equilateral triangles). Interestingly enough, the hieroglyphic sign denoting Sirius was a triangle in ancient Egypt.
The connection is made evident by archaeo-astronomy. First, it is widely accepted these days that the 'air shafts' inside the Great Pyramid were designed to aligned with certain stars. One was specifically targeted toward Sirius in c. 2350 BC.
And at that pinpointed time (c. 2350 BC), Sirius and Orion's Alnitak (representing the Great Pyramid as per the Orion Correlation Theory) together produced the angle 19.5° (when Sirius was rising on the Giza horizon).[10]
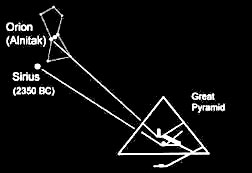 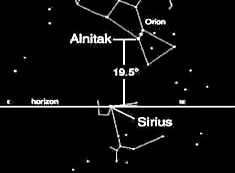
Next, it is natural - given the Sirius-Great Bend connection - to wonder about the possibility of the Nile's 'Winding Waterway' having some relevance to tetrahedral geometry. Indeed, we do find a clear connection!
Believe it or not, the northern peak of the Great Bend precisely pinpoints the tetrahedral/stargate latitude, 19.5°N.!

What's even more incredible is the fact that the same Bend peak also pinpoints 33°E longitude. As those familiar with Hoagland's work would surely know, '33' and '19.5' are considered the two key numbers in the 'hyperdimensional code'! (Hoagland is just not yet aware of this Nile connection.)
In 1997, the esoteric importance of those numbers was overtly demonstrated as NASA landed a tetrahedron-shaped Mars Pathfinder lander on the Red Planet at 19.5 N and 33 W.! (That's pretty in your face, isn't it?)


ORION – The Key To The Kingdom Of Heaven

TEXT TO FOLLOW

EL RIO NILO ES UN REFLEJO ESTELAR ADONDE OBSERVAMOS QUE LA CURVA DEL NILO A 33 ESTE Y 19.47 NORTE ESTA DISEÑADA EN FUNCION A LA SEÑAL DE JONAS. ¿QUE LE QUIERO DECIR CON ESTO? QUE LA POSICION DEL SOL EN LA VIA LACTEA, EN EL CONTEXTO AL RIO NILO, ESTA UBICADA EN FUNCION A LAS PROFECIAS DE CRISTO CON REFERENCIA AL GRIAL. EL ARCA PERDIDA ESPIRITUAL PERDIDO EN ETIOPIA QUE SABEMOS ES JUAN MARCOS. LA VERDADERA ARCA ESPIRITUAL PERDIDA ES EL HIJO DE MARIA LA MAGDALENA Y DE NUESTRO SEÑOR, QUE DESGRACIADAMENTE LA TRADICION PASO POR ALTO YA SEA POR ACCION O POR OMISION.
| phi in Simple Gematria Equals: 33 |
( |
p
16 |
h
8 |
i
9 |
) |
| ophir in Simple Gematria Equals: 66 |
( |
o
15 |
p
16 |
h
8 |
i
9 |
r
18 |
) |
66=33X2
JUAN MARCOS ES EL GRIAL
19+47=66=2X33
The time of the clock on back of the $100 dollar bill, As you can clearly see the time reads 2:22.
19.47 x 12.12 yrs = 235.9764 yrs = 235 yrs and 356 days
December 31, 1776 + 235 yrs and 356 days = December 21, 2012
19.47 x 12 yrs = 233.64 yrs = 233 yrs and 233 days
July 4, 1776 + 233 yrs and 233 days = February 22, 2010
.jpg)  
LA VIUDA PIDE JUSTICIA
Lucas
18:1 También les refirió Jesús una parábola sobre la necesidad de orar siempre, y no desmayar,
18:2 diciendo: Había en una ciudad un juez, que ni temía a Dios, ni respetaba a hombre.
18:3 Había también en aquella ciudad una viuda, la cual venía a él, diciendo: Hazme justicia de mi adversario.
18:4 Y él no quiso por algún tiempo; pero después de esto dijo dentro de sí: Aunque ni temo a Dios, ni tengo respeto a hombre,
18:5 sin embargo, porque esta viuda me es molesta, le haré justicia, no sea que viniendo de continuo, me agote la paciencia.
18:6 Y dijo el Señor: Oíd lo que dijo el juez injusto.
18:7 ¿Y acaso Dios no hará justicia a sus escogidos, que claman a él día y noche? ¿Se tardará en responderles?
18:8 Os digo que pronto les hará justicia. Pero cuando venga el Hijo del Hombre, ¿hallará fe en la tierra?
55. Mateo 23:14: ¡Ay de vosotros, escribas y fariseos, hipócritas! porque devoráis las casas de las VIUDAs, y como pretexto hacéis largas oraciones; por esto recibiréis mayor condenación.
56. Marcos 12:40: que devoran las casas de las VIUDAs, y por pretexto hacen largas oraciones. Estos recibirán mayor condenación.
65. Lucas 20:47: que devoran las casas de las VIUDAs, y por pretexto hacen largas oraciones; éstos recibirán mayor condenación.
¿"Devoran la casas de las viudas" no es una alusion a que devoran la casa/linaje de la viuda? ¿Porque Jesucristo incluso relaciona la viuda con JUAN MARCOS en Hechos 12:12?
1. Hechos 12:12: Y habiendo considerado esto, llegó a casa de María la madre de Juan, el que tenía por sobrenombre MARCOS, donde muchos estaban reunidos orando.
Es obvio que MARIA LA MADRE DE JUAN ES LA VIUDA.
¿PORQUE SE RELACIONA LA VIUDA CON LA EXPULSION DE LOS MERCADERES DEL TEMPLO? ¿HAY UNA CONSPIRACION CONTRA LA VIUDA? ¿QUE PIENSA USTED?
1. Isaías 56:7: yo los llevaré a mi santo monte, y los recrearé en mi casa de oración; sus holocaustos y sus sacrificios serán aceptos sobre mi altar; porque mi casa será llamada casa de oración para todos los pueblos.
2. Mateo 21:13: y les dijo: Escrito está: Mi casa, casa de oración será llamada; mas vosotros la habéis hecho cueva de ladrones.
3. Marcos 11:17: Y les enseñaba, diciendo: ¿No está escrito: Mi casa será llamada casa de oración para todas las naciones? Mas vosotros la habéis hecho cueva de ladrones.
4. Lucas 19:46: diciéndoles: Escrito está: Mi casa es casa de oración; mas vosotros la habéis hecho cueva de ladrones.
ORACION=ORION
NUMERO 33 (RELACION CON EL PERIODO SIDEREO DE MERCURIO) / ESTRELLA DE DAVID / INTERRELACION CON ORION EN FUNCION AL AFELIO Y PERIHELIO DE MERCURIO
En aquel tiempo, respondiendo Jesús, dijo:
Te alabo, Padre, Señor del cielo y de la tierra,
que hayas escondido estas cosas (la Gnosis, la Sabiduría Oculta)
de los sabios (de los eruditos) y de los entendidos, (de los intelectuales)
y las hayas revelado á los niños. (A los Iniciados). Así, Padre, pues que así agradó en tus ojos."
(Mateo 11: 25-26). (El cielo y la tierra, es la alquimia, osea la ESCALERA DE JACOB. La cuadratura del circulo es el patron matematico de la alquimia y esta basado, insisto, en el numero de oro. Justamente Salomon es un tipo del GRIAL.)
"¡Oh profundidad de las riquezas de la sabiduría (sophia)
y de la ciencia (gnwsiV, gnosis) de Dios!
¡Cuán incomprensibles son sus juicios, e inescrutables sus caminos!"
(Romanos, 11: 33). (Camino es una referencia a MERCURIO y Juicio es una referencia a ORION=ESPADA. EL NUMERO 33 NO ESTA POR CASUALIDAD. ES UNA REFERENCIA A LA ESTRELLA DE 6 PUNTAS. OSEA QUE EN LA MISMA PALABRA ESTA CODIFICADA LA RELACION ORION-MERCURIO-VIA LACTEA. PENSAR QUE HAY IGNORANTES QUE DICEN QUE LOS ESCRITORES DE LA BIBLIA NO CONOCIAN EL PI. ESA ES LA SOBERBIA DEL SER HUMANO QUE SE CREE TENER MAS DERECHOS QUE EL CREADOR. ASI ESTA EL MUNDO. SOLO EN JESUCRISTO ESTA LA VERDADERA LIBERACION DE LA EGOLATRIA, IDOLATRIA Y DEL PECADO.)

ESPADA=ORION
This shows Mercury's Inferior Conjunctions with Earth which make a triangle.
Now here are Mercury's Superior Conjunctions with Earth that make an inverted triangle.
Here is what we get when both of these synodic periods are added together.
The star of David.
|
|
|
|
|
ALQUIMIA-DIMENCIONES DE LA GRAN PIRAMIDE-RELACION CON EL 911, CON LAS DIMENCIONES DE LA TIERRA Y LA LUNA Y CON EL CHIVO EXPIATORIO (DIA DE LA EXPIACION)-PATRON GIZE-MENSAJE ROSE LINE DECODIFICADO PARA GLORIA DE YHWH TODOPODEROSO-RELACION CON EL 911 O 711 (11 DE SEPTIEMBRE)
DIAMETRO TIERRA=7920 millas inglesas=720x11
RADIO TIERRA=3960 millas inglesas
RADIO LUNA=1080 millas inglesas
ALTURA PIRAMIDE=3960+1080 millas=5040 millas=720X7
EL 11 DE SEPTIEMBRE O 11/7 ESTA CODIFICADO EN LA GRAN PIRAMIDE DE GIZE EN FUNCION AL RADIO DE LA TIERRA Y DE LA LUNA.
NUMERO DE ORO PHI= (RAIZ CUADRADA DE 5040 ELEVADO AL CUADRADO MAS 3960 AL CUADRADO)/ 3960 = 1.618033
(3960 * 3960) + (5040 * 5040) = 41083200
SQRT 41083200= 6409.61
El radio de la tierra mas el radio de la luna equivalen al RADIO DEL CIRCULO, CUYA CIRCUNFERENCIA EQUIVALE AL PERIMETRO DEL CUBO QUE CONTIENE LA TIERRA. (ALQUIMIA)
LA GRAN PIRAMIDE, EN FUNCION AL NUMERO DE ORO, ESTA DISEÑADA EN EL CONTEXTO A LA DIVISION DEL APOTEMA SOBRE EL RADIO DE LA TIERRA QUE EQUIVALE A LA MITAD DEL LADO DEL CUADRADO DE SU SUPERFICIE.
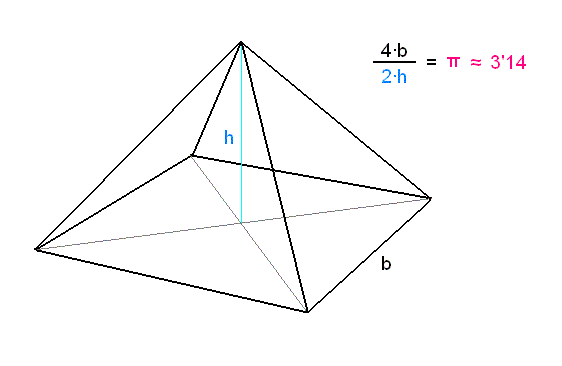

La base de la Gran Pirámide es un cuadrado de 230 metros de lado, caben 8 campos de fútbol. El suelo rocoso donde se asientan las pirámides está exactamente nivelado. El vértice superior de la pirámide a 147 metros de altura coincide con el centro de la base del cuadrado de 230m x 230m.
Medidas según Flanders Petrie
- Lado N: 230,364 m.
- Lado E: 230,319 m.
- Lado S: 230,365 m.
- Lado O: 230,342 m.

Fig 7 . Cuadratura del círculo
El perímetro de la base de la Gran Pirámide es el mismo que el de la circunferencia dada, tomando como radio la altura de ésta, o, lo que es lo mismo, dividiendo el perímetro de la base de la Gran Pirámide por el doble de la altura obtenemos el número Pi.
El perímetro total de la base de la Gran Pirámide p= 23o x 4= 920 metros
Perímetro de la circunferencia 2Пr= 2x(3,1416)x(146,347)= 919,20 metros
Considerando que la base de la GRAN PIRAMIDE TIENE 230 METROS (METRO ESTA DISEÑADO EN FUNCION A ROSE LINE), en el contexto a que EL RADIO ES LA MITAD DEL DIAMETRO, ES OBVIO QUE LA RELACION PROPORCIONAL ES LA MITAD DEL LADO DEL CUADRADO, OSEA 230/2=115 (NUMERO INTERRELACIONADO CON EL PERIODO SIDEREO DE MERCURIO QUE JUSTAMENTE TAMBIEN TIENE REFERENCIA AL NUMERO PI Y CON EL DIA DE SAN MARCOS, OSEA EL 25 DE ABRIL, DIA NUMERO 115 DEL AÑO GREGORIANO. AQUI SE CONFIRMA MATEMATICAMENTE QUE NUESTRO SEÑOR JUSTAMENTE EN MATEO 16:18 ESTABA HACIENDO REFERENCIA A LA GRAN PIRAMIDE Y AL VATICANO, QUE ESTAN DISEÑADOS EN FUNCION A LA CONSTELACION DE LAS PLEYADES Y ORION, EN EL CONTEXTO AL NUMERO DE ORO Y AL GRIAL=JUAN MARCOS.
SI SACAMOS EL APOTEMA tenemos que hacer la RAIZ CUADRADA DE 115 AL CUADRADO MAS 147 AL CUADRADO (TEOREMA DE PITAGORAS) , QUE ES LA ALTURA AL CUADRADO.
115*115+147*147=34834
RAIZ CUADRADA 34834=186.63868837944614 METROS
PHI=186.63868837944614/115=1.62294511634301 (APROXIMADAMENTE PORQUE TOMAMOS NUMEROS REDONDOS PERO ES UNA APROXIMACION DE PHI=1.618033)
INCREIBLE PORQUE EL APOTEMA EQUIVALE A LA CANTIDAD DE DIAS QUE HAY EN EL CALENDARIO LUNI-SOLAR HEBREO DESDE EL PRIMERO DEL PRIMER MES HASTA EL DIA DE LA EXPIACION 9 Y 10 DEL SEPTIMO MES HEBREO QUE FUE EL CORAZON DEL 911.
EL GRIAL, CODIFICADO EN LA BASE DE LA GRAN PIRAMIDE EN EL CONTEXTO AL 911
LEVITICO 23
f) El día de la expiación (YOM KIPUR)
23:26 Habló Yahveh a Moisés, diciendo:
23:27 Además el día décimo de este séptimo mes será el día de la Expiación,  en el cual tendréis reunión sagrada; ayunaréis y ofreceréis manjares abrasados a Yahveh. en el cual tendréis reunión sagrada; ayunaréis y ofreceréis manjares abrasados a Yahveh.
23:28 No haréis en ese mismo día ningún trabajo, pues es el día de Expiación, en el que se ha de hacer la expiación por vosotros   delante de Yahveh, vuestro Dios. delante de Yahveh, vuestro Dios.
23:29 El que no ayune ese día será exterminado de entre su pueblo.
23:30 Al que haga en tal día un trabajo cualquiera, yo lo haré perecer de en medio de su pueblo.
23:31 No haréis, pues, trabajo alguno. Es decreto perpetuo, de generación en generación, dondequiera que habitéis.
23:32 Será para vosotros día de descanso completo y ayunaréis; el día nueve del mes, por la tarde, de tarde a tarde, guardaréis descanso.
23:33 Habló Yahveh a Moisés, diciendo:
EL NUEVE DEL SEPTIMO MES ES EL DIA NUMERO 186 DEL CALENDARIO LUNI-SOLAR HEBREO, EL MISMO DIA DEL 911, EN EL CONTEXTO AL DISEÑO DE LA BASE EN METROS PATRON DE LA MISMA GRAN PIRAMIDE EN EL CONTEXTO A LA VELOCIDAD DE LA LUZ. ESE ES EL VERDADERO MENSAJE DE LA ESTATUA DE LA LIBERTAD
|
|
|
|
|
La Gran Pirámide y el espacio
You are here: Home / La Gran Pirámide y el espacio
El codo real y el metro
La relación entre el codo real y el metro ha sido establecida por los estudios egiptológicos realizados hasta ahora, que se han basado en la medida de varas de madera con marcas en codos reales. El resultado obtenido es 1 codo real = 0,5236 m.
Al respecto, se produce un hecho desconcertante: 0,5236 equivale, a la vez, a Π/6 y a Φ2/5, ya que 3,1416 / 6 = 0,5236 y también 2,6180 / 5 = 0,5236.
Es decir, si dividimos el Número Π entre 6, nos da el mismo resultado que si dividimos el cuadrado del Número de Oro entre 5. Y en ambos casos obtenemos lo que mide un codo real ¡en metros!
Es más, si dibujamos una circunferencia de 1 metro de diámetro y inscribimos un hexágono en la misma, el arco de circunferencia que corresponde a un lado de ese hexágono es igual a 1 codo real (fig. 16).

Figura 16. La relación geométrica entre el codo real y el metro.
El resultado es muy desconcertante porque nos obliga a preguntarnos: ¿el codo real podía obtenerse geométricamente a partir del metro?
¿El metro en la Gran Pirámide?
Una vez reconstruido el modelo de la Gran Pirámide, lo analizamos minuciosamente. Y uno de los resultados más excepcionales obtenidos fue la longitud de la arista. Esta longitud que era especialmente significativa porque elevaba el monumento hacia el cielo, medía exactamente ¡218,00 metros!
Es decir, parecía como si la Gran Pirámide hubiera sido diseñada, a la vez, en codos reales y en metros, ya que las dos principales longitudes que definían su forma se expresaban en números enteros: el lado de la base medía 440 codos reales y la arista, 218 metros.
¿Se podía tratar de una casualidad?
El análisis de las medidas de la Cámara del Rey, que se mantiene intacta en el interior del monumento, insistía triplemente en la presencia de medidas exactas en metros: La altura sobre el zócalo [1] es 43,00 m. La diagonal del muro mayor de la Cámara del Rey mide 12,00 m. Y el volumen de la Cámara es de 321,00 m3.
Por si no fuese suficiente, la suma de la base (440 cr) y la altura (280 cr) de la Gran Pirámide es igual a 720 cr, una medida que coincide exactamente con 377,00 m. Y además da la casualidad que el 377 es el número 14º de la Serie de Fibonacci.

Figura 17. La Cámara del Rey de la Gran Pirámide.
Ante la insistencia de tantas medidas en metros, es obligado que nos preguntemos: ¿los sacerdotes-arquitectos de la Gran Pirámide conocían el metro y lo usaron como segunda unidad de medida al proyectar el monumento?
Para intentar responder a esta pregunta, veamos si las medidas en metros nos proponen juegos numéricos.
Sumemos las 9 longitudes obtenidas: las 4 aristas (4 x 218 = 872 m), más las 4 diagonales de los muros mayores de la Cámara del Rey (4 x 12 = 48 m), más su altura sobre el zócalo (43 m). Resultará 963 m. Y, curiosamente, esta cifra es el triple de 321, el número que expresa el volumen de la Cámara del Rey en m3.
¿Se trata de otra casualidad?
Al llegar a este punto, como había números que establecían juegos entre ellos o se repetían insistentemente en la Gran Pirámide, recordé que Pitágoras [2] estudió en Egipto, donde vivió entre 10 y 20 años, y donde fue ungido sacerdote, por lo que tuvo acceso a sus conocimientos. Por eso no es extraño que el llamado Teorema de Pitágoras se halle en la Gran Pirámide.
Pitágoras y los pitagóricos afirmaban que “todo es número“, por lo que consideraban a los números como divinidades o como entidades abstractas preexistentes e independientes de su unidad de medida.
Este hecho viene confirmado por nuestra cotidiana práctica mental. Si yo levanto la mano y te muestro fijamente la palma abierta con los 5 dedos extendidos, no te preguntaras si es que te estoy saludando, sino que inconscientemente pensarás en el número 5, con independencia de que te esté mostrando 5 dedos.
Lo importante, pues, es el número, no la unidad que expresa. Tanto da que te muestre 5 dedos o 5 lápices, tú pensarás en el número 5.
Basándonos en este concepto, encontraremos otro importante juego numérico, asociado a las medidas enteras que definen el monumento: el lado de la base de 440 cr y la arista de 218 m. La pirámide tiene 4 lados y 4 aristas. El número que se obtiene de la suma de los 4 lados es 4 x 440 = 1.760; y el que resulta de la suma de las 4 aristas es 4 x 218 = 872. Su diferencia es igual a 888.
Y el 888 es el número que contiene la clave de la Gran Pirámide de Keops.
La ley matemática del número 888
Una vez reconstruido el modelo original de la Gran Pirámide y a la vista de los resultados que se iban obteniendo, resultaba imprescindible estudiarlo con detalle. En un primer análisis era necesario obtener y estudiar sus magnitudes: el perímetro, la superficie y el volumen.
A partir de la concepción abstracta del número que nos llega desde los pitagóricos, me decidí a tomar las magnitudes de la Gran Pirámide simplemente como números, con independencia de la unidad de medida que designaban. Y ello dio como resultado una extraña ley asociada a un número singular: el 888.
En la adjunta Tabla de la Gran Pirámide (fig. 18) las magnitudes se hallan en codos reales y en metros. La investigación desarrollada me permitió concluir lo ya intuido: la relación entre el codo real y el metro que los sacerdotes-arquitectos de la Gran Pirámide usaron en el monumento fue 1 codo real = Φ2/5 metros, o lo que es lo mismo, 1 codo real = 2,61803399/5 metros = 0,52360680 metros.
Esta relación es, pues, la que se aplica entre ambas unidades de medida, tanto en el perímetro de la Gran Pirámide, como en su superficie o en su volumen. Por tanto y como es lógico, para transformar codos reales en metros se ha multiplicado la medida en codos reales por 0,52360680; para hacerlo de cr2 a m2, se ha multiplicado los cr2 dos veces por esa cifra, es decir, por su cuadrado; y para pasar de cr3 a m3 se ha multiplicado los cr3 tres veces por la cifra antedicha, es decir, por su cubo.

Figura 18. La Tabla de la Gran Pirámide, con sus magnitudes que cumplen la Ley del 888.
En la tabla adjunta (fig. 18) también se puede aplicar la teoría de conjuntos. Si pongo sobre la mesa una cesta con 3 plátanos, 5 naranjas y 8 manzanas, puedo decir que en la cesta tengo 16 frutas, porque estoy sumando elementos distintos de similar naturaleza.
Es por ello, que tanto si entendemos que las magnitudes son sólo números, como si aplicamos la teoría de conjuntos, podemos sumar codos reales o metros con independencia de que sean lineales, cuadrados o cúbicos. Y es por ello que también podemos sumar los números de las magnitudes obtenidas tal como se hallan en la última columna de la Tabla, donde se suman codos reales y metros.
Observemos las sumas resultantes de cada una de las tres columnas: 18.301.722, 2.671.509 y 20.973.231. Separemos las cifras de 4 en 4, es decir, tomémoslas en unidades de 10.000. En la primera columna resultarán 1.830 y 1.722; en la segunda, 267 y 1.509; y en la tercera, 2.097 y 3.231. Sumemos los números 2 a 2 y obtendremos, en todas ellas, múltiplos de 888, ya que se cumple 1.830 + 1.722 = 3.552 = 888 x 4, y también, 267 + 1.509 = 1.776 = 888 x 2, y finalmente, 2.097 + 3.231 = 5.328 = 888 x 6.
A pesar de haber consultado a cualificados matemáticos, aún ninguno de ellos se ha podido explicar esta ley tan sorprendente. No sabemos cómo los sacerdotes-arquitectos egipcios pudieron establecerla. Y tampoco cómo pudieron llegar a construir la Gran Pirámide a partir de ella.
En el supuesto de que hoy conociéramos la Ley del 888 y, a partir de ella, intentásemos construir una pirámide que tuviera un perímetro, una superficie y un volumen prefijados, sólo podríamos hacerlo mediante sucesivas aproximaciones a través del ordenador. Y quién sabe cuánto tiempo necesitaríamos para conseguirlo y si finalmente lo conseguiríamos.
Por tanto, la Ley del 888 presenta un doble enigma:
¿De dónde procedían los conocimientos matemáticos hallados en la Gran Pirámide?
Los sacerdotes-arquitectos de la Gran Pirámide… ¿Cómo consiguieron diseñar el monumento a partir de tener prefijados su perímetro, su superficie y su volumen por la Ley del 888?
Sin embargo, más allá de los enigmas que abre, la Tabla de la Gran Pirámide nos aporta una importante certeza.
La Ley del número 888 ofrece la prueba irrefutable de que la reconstrucción del modelo original de la Gran Pirámide es totalmente exacta.
Y esta afirmación se basa en que dicha Ley no se cumpliría si hubiera una desviación en el perímetro de la Gran Pirámide de un solo codo real sobre 8.388 cr, o de un solo codo real cuadrado en su superficie sobre 314.159 cr2, o de un solo codo real cúbico en su volumen sobre 17.979.175 cr3, lo que en este último caso representaría que si la exactitud de la reconstrucción fuera de un 99,999994% no sería suficiente para que la Ley del 888 se cumpliese.
Por tanto… ¡La Ley del 888 certifica la reconstrucción exacta del modelo de la Gran Pirámide en sus medidas originales!
Y la Ley del 888 también confirma que en la Gran Pirámide se usó una unidad de medida prácticamente igual a nuestro metro, que establecía la igualdad ya comentada entre 1 codo real y 0,523606797 metros.
|
|
|
|
|
GRAN PIRAMIDE (RELACION CON EL CICLO SINODICO DE MERCURIO Y EL GRIAL)
Noten la relacion de los lados de la GRAN PIRAMIDE que son los mismos lados del cuadrado, osea 230.384 metros. Si consideramos la mitad del mismo, osea 115.192 metros son una obvia referencia a LOS DIAS DEL PERIODO 1/1 hasta el 25/4, osea de 115 dias. En el caso de ser bisiesto seria de 116 dias. Esta impresionante cifra, que es el MISMO CICLO SINODICO DE MERCURIO, RELACIONADO CON EL NUMERO PI en funcion al CICLO DE LA TIERRA ALREDEDOR DEL SOL. Osea que NUESTRO SEÑOR OBVIAMENTE MANEJABA ESTOS CODIGOS CIENTIFICOS EN SU RELACION PEDRO CON EL NUMERO DE ORO (1.618).
 
|
CICLO SINÓDICO DE MERCURIO
|
|
3'14 (pi) ciclos sinódicos en 1 año terrestre.
|
|
|
|
Durante este día 31 de marzo, mientras estás dentro de casa, o dentro de la calle recibiendo los rayos del Sol en la parte de piel no cubierta por la ropa, el propio Sol tiene bajo él a un compañero de la Tierra: es el Planeta Mercurio, que está al otro lado del Sol y un poquito por debajo. Si a la Luna le tocara eclipsar al Sol podríamos ver a Mercurio como un puntito luminoso bajo la Luna y el Sol. Pero eso no ocurre porque la Luna está ocupada en otros asuntos.
Si ahora viajamos a Mercurio y amercurizamos vemos a la Tierra y Venus pasando por detrás del Sol. Si nos llevamos un termómetro, vemos que el mercurio reacciona de forma diferente a como lo hace en la Tierra.
Un momento como este que vemos desde la Tierra con Mercurio al otro lado del Sol es el Punto y Momento Medio del Ciclo Sinódico de Mercurio. Ocurrió hace 116 días, que son 16'6 semanas, y ocurrirá dentro de 116 días. Un ciclo sinódico de un planeta visto desde otro -como la Tierra- no es más que el número días que transcurren entre dos apariciones de ese planeta en el meridiano (línea vertical imaginaria) del Sol, sea por encima, sea a la misma altura del Sol, o sea por debajo. Es una órbita sinódica mientras la órbita real de Mercurio es de 88 días. La diferencia es de 28 días, la media de un mes lunar. Los demás planetas también tienen sus ciclos sinódicos correspondientes: Venus, la Luna, Marte, Júpiter, Saturno, Urano y Neptuno. E igualmente la Tierra vista desde los demás planetas.
Realmente 116 es una media que podemos obtener de un patrón formado por 4 grupos de 3 periodos de diferente número de días pero cuya media es 116 días. Si dividimos 365 días por 116 obtenemos un número conocido, un número universal. Por muy universal que sea no es aplicable a las batallas diarias por la supervivencia en esta extraña y fascinante, necesitada (que no amada) y odiada sociedad que hemos montado en este más o menos olvidado y amado templo de vida que es el Planeta Tierra, compañero y compañera de baile con los demás planetas alrededor del Sol, uno de ellos Mercurio.
Ese patrón regular compuesto por 4 grupos de 3 periodos de número desigual de días que cumple Mercurio durante sus ciclos sinódicos tiene el sentido de servirnos para comprobar -con números y simples operaciones aprendidas en casa y en la escuela- la existencia del equilibrio y la compensación en la Libertad de la Dinámica del Caos del Universo. Los números tienen la función de demostrar lo que nuestra razón no puede. Tales demostraciones pueden servirnos para probar zambullirnos en tal dinámica y comprobar sus resultados en nuestra mente, emociones, organismo, vida, soledad y sociedad. Es como probar a soltarse del flotador y practicar el nado sin apoyarse en algo. O como andar sin apoyarse con las manos, como de peques. Es insólito que un planeta como Mercurio pueda servir para algo.
Esos 4 grupos son los siguientes:
- 1er grupo: 106 días, 126 días y 117 días = 346 días cuya media es 115'3 días.
- 2º grupo: 105 días, 122 días y 121 días = 348 días cuya media es 116 días.
- 3er grupo: 107 días, 118 días y 124 días = 349 días cuya media es 116'3 días.
- 4º grupo: 107 días, 113 días y 127 días = 347 días cuya media es 115,6 días.
Así, la media es 115'8 días, prácticamente 116.
Son 12 ciclos sinódicos de Mercurio distribuidos en 4 grupos de 3 ciclos. El 1er grupo empezó el 22 de febrero de 2007 y el último concluye el 2 de septiembre de 2010. Son 3 años y 7 meses, es decir, 3'6 órbitas de la Tierra y 14'6 de Mercurio. Ahora la Tierra está orbitando en la mitad del 7º ciclo sinódico de Mercurio.
Dado que este momento es el punto medio del ciclo sinódico de Mercurio, su inicio se produjo hace 58 días cuando Mercurio pasó entre el Sol y la Tierra, y su final se producirá dentro de 58 días con el mismo tránsito para iniciar un nuevo ciclo como otra pasada más en un bucle de duración indefinida (que no infinita). Resulta que 58 millones de kms es la distancia media entre Mercurio y el Sol. O 59 días es 1 día en Mercurio.
En la animación se puede observar los movimientos de Mercurio durante una órbita de la Tierra (1 año nuestro). Mercurio da 1 órbita al Sol cuando nosotros cumplimos 88 días y se encuentra 3 veces con la Tierra en el punto más cercano al mismo lado del Sol en 1 año nuestro.
|
MERCURIO
La particularidad de esta línea de perihelio/afelio de Mercurio es que está alineada con la Línea fija formada por Orión/Sol/CentroGaláctico, y como la Tierra pasa cada 19 de junio entre el Sol y el Centro galáctico, eso significa que también en ese día pasa frente al afelio de la órbita Mercurio, y frente al perihelio el 19 de diciembre.
Si "eliminamos" la excentricidad y convertimos la órbita de Mercurio es un círculo racional perfectamente equidistante del Sol, resulta que la órbita de Mercurio inscribe a un pentágono (inscrito en la órbita "perfeccionada" de Mercurio), y este pentágono es la figura interior que resulta de la estrella de 5 puntas formada por la Tierra y Venus durante 8 órbitas de la Tierra y 13 de Venus (8 años), lo cual es el Ciclo Pentagonal.
ENLACES
MERCURIO ERA EL DIOS DE LOS MERCADERES
SAULO/PABLO ES MERCURIO SEGUN HECHOS 14
|
|
|
|
|
PATRON DEL NUMERO OCHO EN EL DISEÑO DE LA GRAN PIRAMIDE-BASE=2 EN EL CUADRADO DE LA PIRAMIDE IDEAL
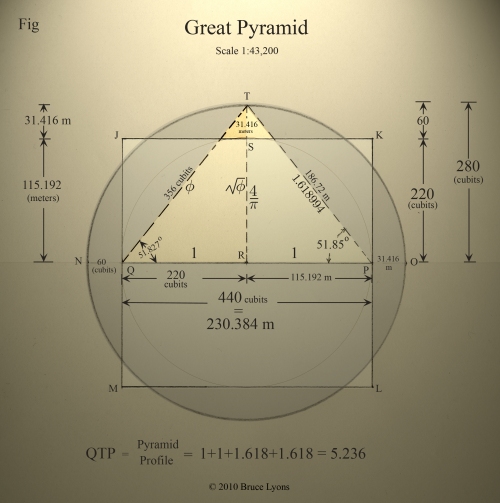
La Gran Pirámide de Keops: pi por la raíz de fi es casi cuatro
Cuaderno de bitácora: publicamos hoy otro de los artículos que en su día aparecieron en doDK. Este artículo fue escrito hace más de seis años. En él explico un descubrimiento que hice por mí mismo, una extraordinaria coincidencia que se da en las proporciones de la Pirámide de Keops y que implica, necesariamente, una no menos extraordinaria coincidencia entre dos de los números más conocidos de las matemáticas.
[Vista de las tres grandes pirámides de la planicie de Giza o Gizeh. No hay que confundirse: la pirámide de Keops, la Gran Pirámide, es la que está más a la derecha, más atrás en la foto. La del medio es la de Kefrén, la segunda en altura, aunque en la foto parece más alta por estar más cerca, y la tercera la de más a la izquierda, la de Micerinos. La pirámide de Kefrén es muy fácil de reconocer porque conserva en su parte superior algo del revestimiento original. Es muy frecuente que se hable de la Gran Pirámide de Keops y sin embargo en las imágenes, erróneamente, aparezca la pirámide de Kefrén, la más fotogénica de las tres]
La gran pirámide de la planicie de Gizeh, la conocida como pirámide de Keops, siempre ha sido una fuente de misterios, y la mayoría están aún por resolver. Sus medidas han sido estudiadas exhaustivamente por todos los inquietos de los enigmas antiguos, y con los datos obtenidos podemos afirmar que los Egipcios no construyeron la pirámide dándole unas medidas al azar, sino que sus proporciones mantienen unas relaciones matemáticas muy interesantes entre sí.
La gran pirámide medía originalmente 147 metros de altura, y el lado de la base tenía una longitud de 230 metros, aproximadamente. Hoy en día la pirámide es un poco más baja, porque a lo largo de los siglos y sobre todo en la Edad Media ha sido utilizada de cantera artificial. Las piedras de las que estaba compuesta se han ido partiendo y tallando en ladrillos más pequeños para servir de material a algunos monumentos levantados en el pasado en la ciudad de El Cairo. Así la pirámide, que en su origen tenía una superficie pulida y blanca y estaba rematada por una punta de oro, se puede contemplar hoy como cuando contemplamos una casa vieja y a punto de derrumbarse, en la que se ven los ladrillos porque la capa de yeso que recubría la pared se ha caído con el tiempo.
Hace ya muchos años descubrí en cierto libro que las proporciones de la pirámide guardaban una importante relación: cuatro veces el lado de la base dividido por dos veces la altura daba el número pi. Esto es lo mismo que decir que si tomamos la altura de la pirámide como radio de una circunferencia, la longitud de la circunferencia coincide con el perímetro de la base.
Si tomamos como datos los que hemos mencionado anteriormente, h = 147 metros, y b = 230 metros. Haciendo la cuenta, 4·b = 920, 2·h = 294, y dividiendo ambas cantidades obtenemos 3'1292517..., es decir, aproximadamente 3'13. Teniendo en cuenta que tanto la altura de la pirámide como el lado de la base se han tomado de forma aproximada, es normal esperar que el resultado no coincida exactamente con el número pi.
Si tomamos en cuenta unas medidas más exactas, como las que aparecen en el libro De las mentiras de la Egiptología a las Verdades de la Gran Pirámide, de Luis García Gallo, la altura sería de 146'7 metros y el lado de la base de 230'4 metros (aproximadamente). Volviendo a hacer los cálculos con estas dos nuevas aproximaciones tenemos que 4·b/(2·h) = 3'14110429... y aquí ya nos vamos aproximando más al número pi. De hecho el error es del orden de 0’016%.
El error es mínimo y totalmente admisible ya que en arquitectura, lo mismo que en todas las demás ciencias aplicadas, las medidas tienen un límite de precisión. De hecho, los cuatro lados de la base de la pirámide no miden exactamente lo mismo, sino que se diferencian en algunos centímetros. De la misma forma las desaparecidas Torres Gemelas no eran exactamente igual de altas, sino que una era un poco más alta (creo que como medio metro) que la otra. A todo esto hay que añadir los estragos del tiempo sobre los monumentos. Las medidas obtenidas son aproximadas sobre una estimación de lo que la pirámide medía cuando la construyeron, hace casi cinco mil años, porque ahora las medidas son muy distintas...
La relación entre b y h se puede expresar así:
Es decir, la proporción entre b y h es como la de pi a 2.
Consultando la página de matemáticas Epsilones descubrí algo nuevo para mí. Según el historiador Heródoto, los Egipcios construyeron la gran pirámide de tal forma que el área de cada una de las caras triangulares laterales coincidiera con el área de un cuadrado de lado igual a la altura.
Teniendo en cuenta lo que acabamos de decir, nos encontramos con las siguientes fórmulas:
Vamos a buscar la proporción entre a, b y h:
Dividimos por b cuadrado y consideramos a/b como una incógnita:
Hemos suprimido la solución negativa porque tanto a como b son números positivos (estamos tratando con longitudes de la pirámide).
De repente nos ha aparecido el número áureo, fi), un número no tan conocido como pi, pero muy importante en la historia de las matemáticas:
De aquí tenemos la relación entre a y b, y por ende entre b y h:
Con esto tenemos que la proporción entre a y b es como la de fi a 2, y la proporción entre b y h es como la de 2 a la raíz cuadrada de fi.
Resumiendo, si los Egipcios construyeron la pirámide con las proporciones mencionadas por el historiador Heródoto, entonces la pirámide de Gizeh es proporcional a una que tenga como altura de una de las caras laterales a fi y como lado de la base a 2:
Entonces surge la cuestión de si ambas propiedades de la pirámide son consistentes, la de pi y la de fi. ¿Cuál de las dos propiedades es la que guió a los constructores de la pirámide? ¿O los constructores quisieron incluir adrede ambas características en su diseño?
Supongamos que somos los constructores, y el faraón nos ordena que levantemos una pirámide en la que el perímetro de la base dividido entre dos veces la altura dé el número pi. Como ya conocemos el número pi, sólo tenemos que preguntarle al faraón la altura que quiere que tenga, y tras unos cálculos sencillos, obtenemos todas las dimensiones, el lado de la base, la longitud de las aristas, etc. Pero el faraón nos dice poco después que además quiere que el área de una de las caras laterales sea igual al área de un cuadrado de lado igual a la altura.
¿Pueden ser posibles ambas cosas? Nosotros ya hemos hecho los cálculos de todas las dimensiones y ya casi nos hemos puesto manos a la obra... Sólo podemos esperar que la suerte nos acompañe y que efectivamente y casi por casualidad se cumpla la segunda condición que nos pide nuestro rey.
¡Y la suerte está de nuestro lado!
Para que se cumpla la condición de pi, b y h tienen que estar en proporción de pi a 2. Para que se cumpla la condición de fi, b y h tienen que estar en proporción de 2 a raíz de fi. Si queremos que se cumplan las dos condiciones, ambas proporciones han de ser iguales:
Bueno, esto no es cierto exactamente, pero sí aproximadamente:
De hecho el error que se comete es menor al 0'1%. Eso quiere decir que con un error del 0'1% podemos construir una pirámide que cumpla las dos condiciones, guardando dentro de sus proporciones al número pi y al número fi. Y la pirámide de Keops es un ejemplo de ello.
Maravilloso, ¿verdad? Y todo porque pi por la raíz de fi es casi cuatro.
Notas: no fui el primero en descubrir esta coincidencia entre los números pi y fi. En el libro de Martin Gardner, Los Mágicos Números del Doctor Matrix, en el capítulo de las pirámides, se habla sobre la curiosa relación entre el número pi y el número fi que posibilita que la Gran Pirámide de Keops cumpla dos propiedades matemáticas diferentes. Sin embargo, honestamente, no leí ese contenido del libro hasta este mismo año pasado, 2009, seis años después de escribir este artículo.
Por otro lado, han quedado plasmados mis esfuerzos para expresar la notación matemática en un artículo de la web. No soy muy experto todavía en esto, y la solución que encontré en su momento fue la de usar el editor matemático del Microsoft Word para escribir la expresión que quería, y luego guardar dicha expresión como archivo de imagen, para incluirlo en el artículo. Los gráficos de las pirámides los realicé con el sencillo programa Paint que viene incluido en Windows.
Para algunas otras curiosidades matemáticas de la pirámide de Keops, entre las muchas que tiene, recomiendo leer mi artículo en el blog Vientos de eternidad.
|
|
|
|
|
IMPRESIONANTE CONEXION FILIPOS (ORACULO DE DELFOS)-SO-PHI-A /1.618-ES OBVIO EN ESTE MARCO QUE NUESTRO SEÑOR HACIA REFERENCIA A MARCO ANTONIO EN MATEO 16:18-SECRETO DEL APOLO 11 DECODIFICADO-
triángulos isósceles
 |
| el templo de Athena Afaia en la isla de Aegina |
Uno del más famosa tales colocaciones es el triángulo isósceles entre el acropolis de Atenas, el templo de Poseidon en Sounion y el templo de Afaia Athena en Aegina con la distancia del estadio 242. Si era el único que podría ser justo una coincidencia pero tenemos más triángulos interesantes…
Relacionan la mayoría de ellos con Delos, Delphi y Dodoni. ¡Es otra coincidencia interesante que estos tres nombres están utilizando como primero ponen letras a la D, delta en griego, esta letra se escriben como triángulo isósceles también!

Delphi
 |
| ciudades con la misma distancia de Delphi |
El oráculo de Delphi fue creído para ser el ombligo del mundo. Pues un símbolo él recuerda a nosotros el nacimiento humano donde el ombligo pasa la vida de la madre al niño y también al punto del balance del peso que es el ombligo para el ser humano.
Aquí son algunas ciudades que tienen distancia igual del Delphi.
Como una unidad que mide nosotros utiliza el estadio = 185.2 metros.
- Atenas - Olympia (660 estadios)
- Eleusis - Iolkos (550 estadios)
- Megalopoli - Figaleia (660 estadios)
- Idaio Andro (Crete) - Smyrna (2198 estadios) - triángulo equilátero
- Pella - Corfu, (1350 estadios)
- Kinira (Thasos) - Kardamili (Hios) (1700 estadios)
- Dodoni - Dion (estadio 1010, 187 kilometerss)
 http://www.ancient-technology.com/ancient_technology_es/geometry.asp http://www.ancient-technology.com/ancient_technology_es/geometry.asp
Romanos 11:33: ¡Oh profundidad de las riquezas de la sabiduría y de la ciencia de Dios! ¡Cuán insondables son sus juicios, e inescrutables sus caminos!
FI=PHI=NUMERO DE ORO=1.618033
171. Salmos 45:9: Hijas de reyes están entre tus ilustres;Está la REINA a tu diestra con oro de Ofir.
SO-FI-A/SABIDURIA/S-OFI-A/FI-L-OFI-A
REINA VESTIDA CON ORO DE O-FI-R
triángulos isósceles
 |
| el templo de Athena Afaia en la isla de Aegina |
Uno del más famosa tales colocaciones es el triángulo isósceles entre el acropolis de Atenas, el templo de Poseidon en Sounion y el templo de Afaia Athena en Aegina con la distancia del estadio 242. Si era el único que podría ser justo una coincidencia pero tenemos más triángulos interesantes…
Relacionan la mayoría de ellos con Delos, Delphi y Dodoni. ¡Es otra coincidencia interesante que estos tres nombres están utilizando como primero ponen letras a la D, delta en griego, esta letra se escriben como triángulo isósceles también!

Delphi
 |
| ciudades con la misma distancia de Delphi |
El oráculo de Delphi fue creído para ser el ombligo del mundo. Pues un símbolo él recuerda a nosotros el nacimiento humano donde el ombligo pasa la vida de la madre al niño y también al punto del balance del peso que es el ombligo para el ser humano.
Aquí son algunas ciudades que tienen distancia igual del Delphi.
Como una unidad que mide nosotros utiliza el estadio = 185.2 metros.
- Atenas - Olympia (660 estadios)
- Eleusis - Iolkos (550 estadios)
- Megalopoli - Figaleia (660 estadios)
- Idaio Andro (Crete) - Smyrna (2198 estadios) - triángulo equilátero
- Pella - Corfu, (1350 estadios)
- Kinira (Thasos) - Kardamili (Hios) (1700 estadios)
- Dodoni - Dion (estadio 1010, 187 kilometerss)
 http://www.ancient-technology.com/ancient_technology_es/geometry.asp http://www.ancient-technology.com/ancient_technology_es/geometry.asp
|
|
FILIPOS ESTA EN EL MISMO PARALELO QUE EL VATICANO (PARALELO 41)
Filipos (ciudad)
De Wikipedia, la enciclopedia libre
Para otros usos de este término, véase Filipo. Filipos (latín Philippi, griego Φίλιπποι, Phílippï) fue una ciudad de Macedonia oriental fundada por Filipo II de Macedonia, que le dio su nombre (antes se llamaba Crénides, latín Crenides, es decir, lugar de las fuentes, por las diversas fuentes del río Angites). Cerca había minas de oro, especialmente las de Asyla. Estaba cercana al río Gangas o Gangites.
Filipos es una fundación del rey de Macedonia, Filipo II, en el lugar de la colonia tasia de Crénides (Κρηνἱδες), en el valle del monte Orbelos (nombre antiguo del monte Lekani), en el borde norte de la marisma que ocupaba en la antigüedad toda la llanura que lo separaba del monte Pangeo al sur.
El objetivo de esta fundación era tanto tomar el control de las minas de oro vecinas como establecer una guarnición en un punto de paso estratégico: el sitio controlaba la ruta entre Anfípolis y Neápolis, un segmento de la gran carretera real que atravesaba de este a oeste, Macedonia y que será más tarde reconstruida por los romanos bajo el nombre de Vía Egnatia
Filipo II dotó a la nueva ciudad de importantes fortificaciones, que cortaban en parte el paso entre las marismas y el Orbelos, y envío allí colonos. Hizo emprender el saneamiento de las marismas, de lo que da testimonio al escritor Teofrasto. Filipos conservó una verdadera autonomía dentro del Reino macedonio: una ciudad con sus propias instituciones políticas (ekklesía del demo). El descubrimiento de nuevas minas de oro cerca de la ciudad, en Asyla, contribuyó al enriquecimiento del reino de Filipo II, que estableció allí un taller monetario. La integración definitiva de la ciudad en el reino macedonio tendría lugar bajo Filipo V.
La ciudad fue a pesar de todo de tamaño modesto (¿2.000 habitantes?): cuando los romanos destruyeron definitivamente el reino argéada de Macedonia en 167 a. C. y lo dividieron en cuatro estados distintos (merides), fue Anfípolis y no Filipos la designada como capital del estado de Macedonia oriental.
No se conoce nada o casi nada de la ciudad en esta época, excepto el recinto, el teatro, los cimientos de una casa bajo el foro romano, un pequeño templo y sobre todo un heroón (templo consagrado a un héroe). Este monumento recubre la tumba de un tal Exekestos quizás situada en el ágora, y ligada al culto de κτίστης (ktístès) (héroe fundador) de la ciudad.
Hacia el 400 a. C. pasó a Tasos. Después pasó a Filipo II que explotó las minas y obtenía 1000 talentos al año. Después de la conquista macedonia de Anfípolis, Pidna y Potidea, la ciudad fue agrandada y fortificada para defenderla de las tribus tracias.

Vestigios del centro de la ciudad: foro en primer plano, mercado y basílica B al fondo.
Fue visitada en algunas ocasiones por el apóstol Pablo (49, 56 y 57). Cuando Macedonia fue dividida en dos provincias por Teodosio el Joven, Filipos fue la capital de Macedonia Primera.
La ciudad reaparece en las fuentes con ocasión de la guerra civil romana que siguió al asesinato de Julio César. Sus herederos Marco Antonio y Octavio se enfrentaron a los partidarios de la República, Marco Junio Bruto y Cayo Casio Longino, en una doble batalla decisiva en la llanura al oeste de la ciudad en octubre de 42 a. C.
Un bando estaba dirigido por Augusto y el otro por Bruto; en un primer combate este último venció, pero en el segundo, veinte días después, fue derrotado. Vencedores, Marco Antonio y Octavio licenciaron una parte de sus veteranos, probablemente de la legio XXVIII, los cuales se instalaron en la ciudad, refundada como colonia romana bajo el nombre de Colonia Victrix Philippensium.
Augusto le dio entonces, (41 a. C.) el rango de colonia (Colonia Victrix Philippensium) con derecho italiano. En 30 a. C., Octavio reorganizó la colonia y procedió a un nuevo licenciamiento de veteranos, quizás de pretorianos y de italianos: la ciudad tomó el nombre de Colonia Iulia Philippensis, convertido en Colonia Augusta Iulia Philippensis después de enero de 27 a. C., cuando Octavio recibió él mismo el nombre definitivo del Senado.

Basilíca B vista del suroeste, y acrópolis al fondo.
Pablo habría visitado la ciudad en otras dos ocasiones, en 56 y 57. La epístola a los filipenses dataría de 54-55 y testimonia el impacto inmediato de la palabra paulina. El desarrollo subsecuente del cristianismo en Filipos está bien atestiguado, sobre todo por una carta de Policarpo de Esmirna dirigida a la comunidadd filipense hacia el 160, y por la epigrafía funeraria.

Inscripción del obispo Porfirio en la Basílica de Pablo.
. El parentesco del plano y de la decoración arquitectónica de la basílica B con Santa Sofía y Santa Irene de Constantinopla otorgan un lugar privilegiado a esta iglesia en la historia del arte paleocristiano. El complejo episcopal que toma el lugar de la Basílica de Pablo a partir del siglo V, construida alrededor de una iglesia octogonal, rivaliza también con las iglesias de la capital.
MARY MAGDALENE (ESTRELLA DE OCHO PUNTAS)-OCTAVO DIA
En la misma época, las murallas de la ciudad son reconstruidas para hacer frente a la inseguridad creciente en los Balcanes. ·n 473, la ciudad es sitiada por los ostrogodos que no llegan a tomarla pero queman los arrabales.
|
|
|
|
|
La conexion MATEO 16;18 esta en el contexto a LA BATALLA DE FILIPO Y MARCO ANTONIO. EL ARCA DE NOE TAMBIEN ESTA DISEÑADA CON EL PATRON DE LA SERIE DE FIBONACCI. ESTO EXPLICA DESDE OTRA PERSPECTIVA LA RELACION COLUMBIA CON EL APOLO 11 (ORACULO DE DELFOS).
|
|
|
|
|
|
|
Poussin's Moses left by the river  Alpheus Ovid's Metamorphoses tells his story. He pursued a beautiful young woman, Arethusa, who swam in his waters. She appealed to Artemis, goddess of the hunt, to escape him and was transformed also into water. But to aid her escape Artemis split the earth underground between Greece and Sicily, allowing Arethusa to flow through this hidden passage and emerge as a spring in Sicily, the source of some of the purest and most sought-after waters on the island, a spot now sacred to Artemis and named after Arethusa. But Alpheus followed, intermingling his waters with hers, and legend has it that a wooden cup dropped in the river Alpheus in Greece can re-emerge in Sicily. (Cf. Edith Hamilton's Mythology.) the river god holding the horn of plenty and the Sphinx pagan imagery with a Jewish Christian theme Imagery found in Rome...as well as Egypt and the river god is found in Montreal spilling water in the fountain in front of Notre Dame Basilica Alpheus is seen in Et in Arcadia Ego http://www.swarthmore.edu/Humanities/ps ... rgod2.htmlThe Egyptian Pyramids in the background One is a square pyramid found in Giza Egypt  It is near the Nile The other pyramid Nubian  he most extensive Nubian pyramid site is at Meroë, which is located between the fifth and sixth cataracts of the Nile, then there is a Circular Tower Acadia has a river ....the Mississippi where Cahokia Mounds are found next to the river Salz (Sals) river running red.....Moses made the Nile red like Blood the video says it was the day the Pope was elected http://youtu.be/h79D8rpsEM4Poussin places the geometrical structures in his painting
_________________
Everything is Connected and there are no
coincidences
|
|
|
|
|
TEOTIHUACAN-GIZE-NUMERO DE ORO PHI=1.618-RELACION CON LA INDEPENDENCIA DEL ESTADO DE ISRAEL
ISRAEL
ISIS
RA
ELOHIM
330 AÑOS EXACTOS MAS 1618=1948 (INDEPENDENCIA DE ISRAEL)





¿Qué es phi?
Phi y la serie de Fibonacci
Funciones trigonométricas
Razones matemáticas
Pentágono
Espirales Áureas
Inicio :: Ver temas relacionados: Decalogo Geometria Sagrada :: Número de Oro :: Merkaba
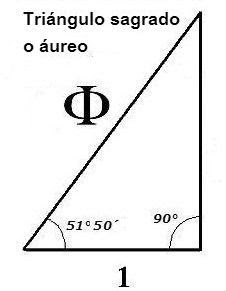
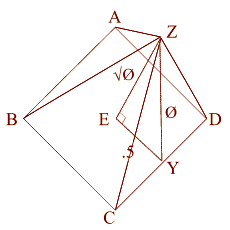
¿Qué es phi?
Phi (1.618033988749895... ), pronunciado como fi, es un numero irracional como Pi ( 3.14159265358979... ), pero con muchas características matemáticas inusuales. Phi es la base de la Proporción Dorada. La razón o proporción determinada por Phi (1.618...) era conocida por los Griegos como la “Sección Dorada” y por los artistas del renacimiento como la “Proporción Divina”. También se le conoce como la razón Dorada o la Proporción Áurea.
Phi, como Pi, es una razón definida por una construcción geométrica.
Pi es la relación de la circunferencia de un círculo respecto a su diámetro. Phi es la proporción de los segmentos de una línea que resultan cuando una línea es dividida de una forma única y especial.
La línea es dividida para que la proporción de la longitud de la línea entera (A) respecto a la longitud del segmento de la línea mayor (B) sea igual que la proporción de la longitud del segmento de la línea mayor (B) a la longitud del segmento de la línea menor (C)

Esto es que A es 1.618... veces B, y B es 1.618… veces C. Recíprocamente, C es 0.618... de B y B es 0.618... de A. Phi con mayúscula "Phi" es 1.6180339887..., mientras que phi con minúscula es 0.6180339887, el reciproco de Phi o Phi menos 1.
Lo que hace a phi incluso mas inusual es que puede derivarse de muchas formas y ser encontrado en proporcionalmente en el universo. Phi F puede ser derivado por: la serie numérica descubierta por Leonardo Fibonacci, matemáticas y geometría.
Phi y la serie de Fibonacci
Leonardo Fibonacci, por herencia del mundo árabe, descubrió la serie que nos lleva a phi. En el siglo XII, Leonardo Fibonacci descubrió una serie numérica simple que es la base de la increíble relación que encontramos detrás de phi. Empezando con 0 y 1, cada número de la serie es simplemente la suma de los dos anteriores. Así: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, . . .
La razón (proporción) de cada par sucesivo de números en la serie se aproxima a phi (1.618. . .). Así si dividimos 5 entre 3 es 1.666..., y 8 entre 5 es 1.60. En la medida en la que vamos mas lejos del 0 (punto de inicio de la secuencia) nos acercamos al valor de phi.
La tabla de abajo nos muestra como las proporciones de números sucesivos en la serie Fibonacci se aproxima a Phi.
Puedes computar cualquier número de la serie Fibonacci fácilmente. Usa phi para saber cualquier numero (n) de la serie Fibonacci (f)
fn = Fn / 5½
Phi puede derivarse matemáticamente resolviendo la ecuación:
n2 - n1 - n0 = 0 que es lo mismo que n2 - n - 1 = 0
Esta ecuación la rescribimos y nos queda así:
n2 = n + 1 y 1 / n = n - 1
La solución a la ecuación es la raíz cuadrada de 5 más 1 dividido entre 2
( 5½ + 1 ) / 2 = 1.6180339... = F
Esto resulta en dos propiedades únicas de phi:
Si elevas al cuadrado a phi, obtienes un numero exactamente 1 mayor que phi: 2.6180...
F2 = F + 1
Si divides a phi entre 1, obtienes un numero exactamente a 1 menos phi: 0.6180...:
1 / F = F - 1
Phi, curiosamente, puede ser expresado en cinco: 5 ^ .5 * .5 + .5 = F
Puedes usar phi para computar un número n en la serie Fibonacci (fn): fn = Fn / 5½
Como por ejemplo, el número 40 de la serie Fibonacci es 102, 334, 155, que puede expresarse
f40 = F40 / 5½ = 102,334,155
Este método en realidad nos provee un estimado que siempre esta cerca del numero correcto Fibonacci.
http://www.iuca.net/gs/que%20es%20phi.htm









¿Qué es phi?
Phi y la serie de Fibonacci
Funciones trigonométricas
Razones matemáticas
Pentágono
Espirales Áureas
Inicio :: Ver temas relacionados: Decalogo Geometria Sagrada :: Número de Oro :: Merkaba
¿Qué es phi?
Phi (1.618033988749895... ), pronunciado como fi, es un numero irracional como Pi ( 3.14159265358979... ), pero con muchas características matemáticas inusuales. Phi es la base de la Proporción Dorada. La razón o proporción determinada por Phi (1.618...) era conocida por los Griegos como la “Sección Dorada” y por los artistas del renacimiento como la “Proporción Divina”. También se le conoce como la razón Dorada o la Proporción Áurea.
Phi, como Pi, es una razón definida por una construcción geométrica.
Pi es la relación de la circunferencia de un círculo respecto a su diámetro. Phi es la proporción de los segmentos de una línea que resultan cuando una línea es dividida de una forma única y especial.
La línea es dividida para que la proporción de la longitud de la línea entera (A) respecto a la longitud del segmento de la línea mayor (B) sea igual que la proporción de la longitud del segmento de la línea mayor (B) a la longitud del segmento de la línea menor (C)

Esto es que A es 1.618... veces B, y B es 1.618… veces C. Recíprocamente, C es 0.618... de B y B es 0.618... de A. Phi con mayúscula "Phi" es 1.6180339887..., mientras que phi con minúscula es 0.6180339887, el reciproco de Phi o Phi menos 1.
Lo que hace a phi incluso mas inusual es que puede derivarse de muchas formas y ser encontrado en proporcionalmente en el universo. Phi F puede ser derivado por: la serie numérica descubierta por Leonardo Fibonacci, matemáticas y geometría.
Phi y la serie de Fibonacci
Leonardo Fibonacci, por herencia del mundo árabe, descubrió la serie que nos lleva a phi. En el siglo XII, Leonardo Fibonacci descubrió una serie numérica simple que es la base de la increíble relación que encontramos detrás de phi. Empezando con 0 y 1, cada número de la serie es simplemente la suma de los dos anteriores. Así: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, . . .
La razón (proporción) de cada par sucesivo de números en la serie se aproxima a phi (1.618. . .). Así si dividimos 5 entre 3 es 1.666..., y 8 entre 5 es 1.60. En la medida en la que vamos mas lejos del 0 (punto de inicio de la secuencia) nos acercamos al valor de phi.
La tabla de abajo nos muestra como las proporciones de números sucesivos en la serie Fibonacci se aproxima a Phi.
Puedes computar cualquier número de la serie Fibonacci fácilmente. Usa phi para saber cualquier numero (n) de la serie Fibonacci (f)
fn = Fn / 5½
Phi puede derivarse matemáticamente resolviendo la ecuación:
n2 - n1 - n0 = 0 que es lo mismo que n2 - n - 1 = 0
Esta ecuación la rescribimos y nos queda así:
n2 = n + 1 y 1 / n = n - 1
La solución a la ecuación es la raíz cuadrada de 5 más 1 dividido entre 2
( 5½ + 1 ) / 2 = 1.6180339... = F
Esto resulta en dos propiedades únicas de phi:
Si elevas al cuadrado a phi, obtienes un numero exactamente 1 mayor que phi: 2.6180...
F2 = F + 1
Si divides a phi entre 1, obtienes un numero exactamente a 1 menos phi: 0.6180...:
1 / F = F - 1
Phi, curiosamente, puede ser expresado en cinco: 5 ^ .5 * .5 + .5 = F
Puedes usar phi para computar un número n en la serie Fibonacci (fn): fn = Fn / 5½
Como por ejemplo, el número 40 de la serie Fibonacci es 102, 334, 155, que puede expresarse
f40 = F40 / 5½ = 102,334,155
Este método en realidad nos provee un estimado que siempre esta cerca del numero correcto Fibonacci.
http://www.iuca.net/gs/que%20es%20phi.htm





|
|
|
|
|
Torus
The torus is also a very important geometrical three-dimensional form and we’ll bring it up here because it is the building block of matter in the new aether science of the next chapter. It is best compared with a doughnut or the smoke ring from a cigar. Here’s it is:

Torus
It is a sphere, curving inwards on top and bottom, such that it has a hole in the middle! It also resembles an apple. The torus is the result of rotating the Genesis pattern 360 degrees around the center.
Tetrahedron, Cube, Octahedron, Dodecahedron and Icosahedron.

Crop circle, West Overton, 24th June 1999 octahedron projected in 2D layout.
All of these five forms are in the Cube of Metatron, it may take a little while to discover them but they are all in there. The Platonic solids have very remarkable characteristics, for one they all fit perfectly within a sphere. The vertices of the solid are on the surface of the circumscribing sphere! Also they perfectly fit inside each other and can be perfectly nested. All forms have a double, an opposite form that can be created from the other. The cube and the octahedron are doubles for instance. If we take the centers of the faces of the cube and connect all the lines between these centers we get the octahedron. The same process can be reversed creating a cube from an octahedron. The tetrahedron has itself as the double. The dodecahedron and icosahedron are doubles. Every line, face and angle in a Platonic form is identical to every other line, face and angle within the same form. In other words the Platonic solids are extremely symmetrical!
Another puzzling symbol that is derived from the progression of the Flower of Life is the Tree of Life. The Tree of life is central subject of study in the mystical Jewish Kabbalah. The Tree of Life can be overlaid with the Flower of Life and they will perfectly match. The Tree of Life is an extraction from the Flower of Life, leaving out a number of spheres of no interest.
Now the Fruit of Life is called a female form because it only contains rounded forms, spheres, just like a female body that is curved. The male counterpart can be constructed if straight lines are used to connect all the centres of all the spheres in this picture. The result is called the Cube of Metatron.
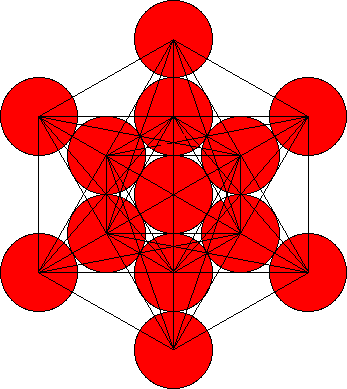
Cube of Metatron
The Cube of Metatron is very important since it contains the solid geometrical forms that have become the focus of a new aether physics that we will describe in the next chapter!
Philosopher Plato described these forms that we find in the Cube of Metatron 400 years BC, hence they are called the Platonic solids.
In fact the Platonic solids can be found in the Metatron twice, the smaller versions of the solids are repeated in the inner 7 spheres. One of the five Platonic solids is the well-known cube. If you will, you can try and find the cube in the Cube of Metatron. I will help you a little bit with this one, here it is:
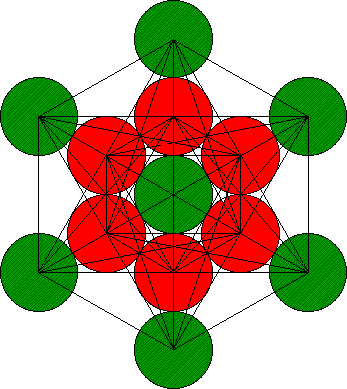
Cube in the Cube of Metatron
The green spheres are the corners of the cube. One corner in the back is hidden from view though.
Platonic solids
The five Platonic solids are named after Greek philosopher Plato who first described them 350 years BC in his book Timaeus. Here they are:
|
|
|
Golden Mean
Maybe the most important subject of sacred geometry is the Golden Mean. The Golden Mean is a very special ratio and is expressed by the Greek letter Ф called Phi.
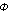 = ½ * v5 + ½ = 1.618 = ½ * v5 + ½ = 1.618
Phi like Pi is an irrational number, meaning you can never calculate its exact value, you can only approximate it.
The Phi ratio is expressed in the Golden Section. The Golden Section is a the length of let’s say a rope when it is divided such that the ratio of the longer part of the rope to the whole is exactly the same ratio as the shorter part of the rope is to the longer part. (Read it again)
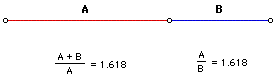
When the Phi ratio is applied to a rectangle whereas B = 1 and A has length Ø, the rectangle is called a Golden Rectangle.
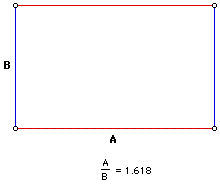
The Golden Rectangle can be used to create a spiral, the Golden Spiral. Starting with one Golden Rectangle, a second Golden Rectangle can be attached to the first using the longest side of the rectangle, side A as the shortest side B of the next rectangle. To this end the second rectangle is constructed 90 degrees perpendicular to the first rectangle. If this process is continued, called the spiralling of the Golden Rectangle, a curved line can be drawn through the corners of the rectangles creating the Golden Mean spiral. The spiralling of the Golden Mean spiral continues indefinitely in inward and outward directions, it’s getting smaller and smaller spiralling inwards and getting bigger and bigger spiralling outwards.
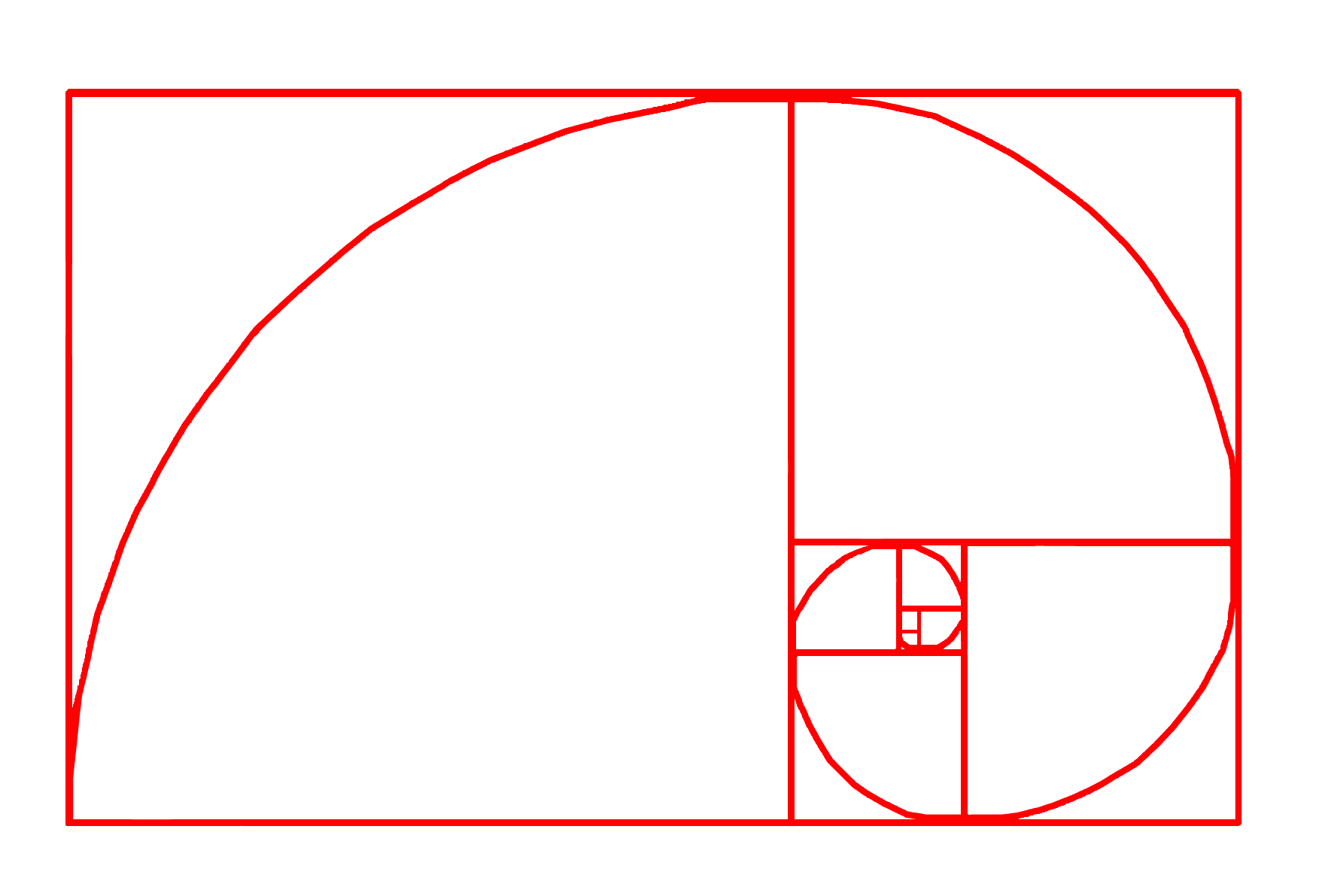
Golden Mean spiral
A variant of the Golden Mean spiral is the Fibonacci spiral. The difference with the Golden Mean spiral is that is does not spiral in indefinitely but starts with a Golden Rectangle of which one side has length 1 and the other length Phi.
Gradually when the Fibonacci spiral, spirals outward, there will be no distinction noticeable any more between a true Golden Mean spiral and the Fibonacci spiral. The Fibonacci spiral is based on the progression of the Fibonacci sequence.

Crop circle, fractal spirals, Milk Hill, Wiltshire august 12th 2001
Fibonnaci sequence
Leonardo Fibonacci (1175 AD), a great mathematician of the Middle Ages discovered the Fibonacci sequence by studying nature. He studied the growth of rabbit populations and the growth of leaves and petals and discovered a well-defined mathematical sequence in all of this.
This is the Fibonacci sequence:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 etc.
Each number in the sequence is the sum of the two preceding numbers starting with the root number 1. The Fibonacci sequence progresses towards the Golden Mean if we divide two successive numbers in the sequence.
1/1 = 1
2/1 = 2.0
3/2 = 1.5
5/3 = 1.667
8/5 = 1.60
.
144/89 = 1.618
The Fibonacci sequence propagates towards Phi (Ø) but never reaches it since it is an irrational or transcendent number.
Fibonacci spirals and Golden Mean ratios appear everywhere in the universe. The spiral is the natural flow form of water when it is going down the drain. It is also the natural flow form of air in tornados and hurricanes. Here’s another beautiful example of a Fibonacci spiral in nature, it’s the Nautilus shell and every book about sacred geometry contains one:

Nautilus shell
The Golden Mean ratio is all over the human body, in the ratios between the bones, the length of your arms and legs. The Golden Mean is also the ratio in the distance from the navel to your toe and the distance from your navel to the top of your head. Michelangelo has beautifully hidden these Golden Mean ratios in his fresco on the ceiling of the Sistine Chapel in Rome:
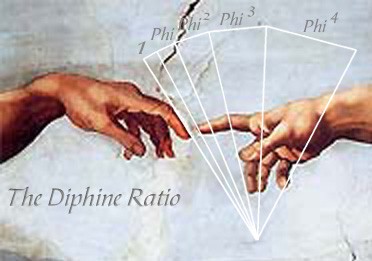
Michelangelo and the Phi ratios in the human hand
(Courtesy of Frank van den Bovenkamp, www.frankvandenbovenkamp.com)
Music
Greek philosopher Pythagoras discovered a wonderful mathematical relation between the harmonic notes in music. He noticed that by depressing a string in different positions on the fingerboard of a guitar like string instrument that harmonic sounds were created. Some notes sounded better than others. At each depression of the string the string is divided in two different lengths and the ratio between these lengths were measured by Pythagoras. He marked down all the ratios that sounded harmonically well together. In this way he found the following ratios:
1:1 (open snare)
1:2 (depressed at 1/3 of the length of the string)
3:2 , 5:3, 13:8, 21:13, 34:21
What Pythagoras had discovered is called the Diatonic musical scale, named after the fact that the string is divided into two lengths (Dia = two).
These ratios correspond with the frequencies of the notes produced by the white keys of the piano when attuned in the Diatonic scale. After the 7th note the octave of 8 notes is repeated only this time the first and the eighth note are doubled in frequency! The next 7 notes of the white keys on the piano follow the exact same ratio!
Now if you have been paying attention you may already have noticed that the musical ratios discovered by Pythagoras are the same ratios of the Fibonacci sequence! Simply take a number out of the Fibonacci sequence and its successor and you have the musical ratio found by Pythagoras.
The Fibonacci sequence is the sequence that gives us beautiful harmonics in music. The diatonic scale is not the only musical scale, there are many more, in fact no piano today is tuned in the Diatonic scale. But the principle relation between harmonics in music and mathematical progressions of the Fibonacci sequence is real.
Now let’s pretend that we’ve tuned a piano in the Diatonic scale and that we have extended the piano’s keyboard with keys to provide for 49 octaves! That would be one hell of a piano and it would certainly no longer fit into your living room!
But suppose that we could actually play on this piano. When we play the notes in the last two highest octaves, the keys on the furthermost right side of this piano, will correspond with the frequencies of the colours of light!
There are seven keys in the highest octave that are the frequencies of the 7 primary colours of the spectrum of light, the 7 colours of the rainbow!
So not only does the Fibonacci sequence define the ratios of harmonics in sound but also in the electromagnetic spectrum of light, it defines the 7 colours of the rainbow!

Music and color, the same harmonic ratios
We now know that many musicians like Beethoven, Mozart, Chopin, Bartók, Schubert and Debussy used the Fibonacci sequence and the Golden Mean ratio deliberately not in the notes but in the composition itself. For instance Beethoven used the Golden Mean in his famous Beethoven’s Fifth. His famous opening motto not only appears on the first and the last bar of the symphony but also on the bar that represents the exact Golden Mean point of his symphony! Bela Bartók used both the Golden Mean and the Fibonacci sequence deliberately in his compositions using the measures 5, 8, 13, 21, 34, 55 and 89 to introduce new instruments such as strings, cellos, percussion etc. The question is why did these composers add sacred geometry into their music? Maybe they were not only famous musicians but also Freemasons?
Squaring the circle

A classical mathematical problem dating all the way back to Plato is called ‘squaring the circle’. In the last three thousand years mathematicians have tried to come up with a solution using only a pair of compasses and straightedge on how the construct a circle and square such that they have the same perimeter. In 1882 Lindemann proved that there is no solution to this problem. Since Lindemann’s proof is rather complex, we will show in simple terms why the circle cannot be squared. The circumference of the circle with a radius of one is 2 * π and π (Pi) is an irrational number (a transcendent number, π can never be measured only be approximated!). But when Pi is irrational and cannot be measured so is the circumference of the circle! However the square’s circumference is a real number since it equals 4 times the side of the square that is a real number that can be measured. Hence the circumference of both circle and square will never be equal in the mathematical sense; however they can become infinitely close.
Vitruvian man
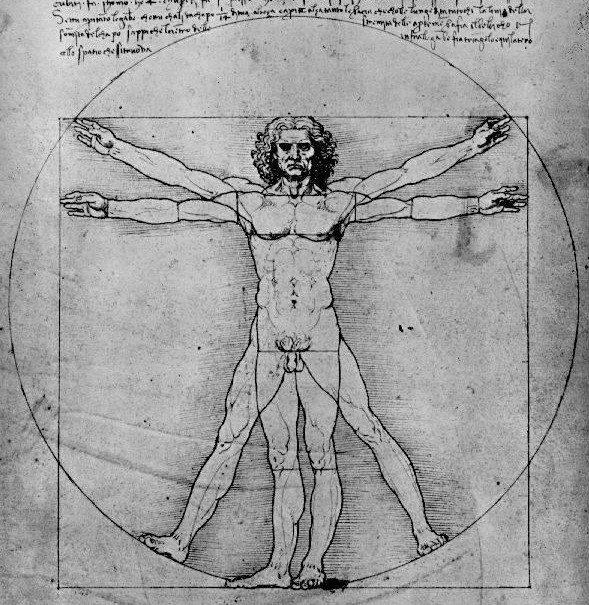
Now here’s an interesting drawing from Leonardo Da Vinci. What he is showing in this sketch is that the human body ‘squares the circle’. When man stretches his arms and holds them horizontally, man’s body will perfectly fit into the square. On the other hand, when he spreads his legs and raises his arms as in the sketch, man’s body can be perfectly circumscribed by a circle. The circumference of the square ‘equals’ that of the circle.
A lot has been written about this sketch alone, it contains a whole lot of hidden sacred geometry. We will not go into all the details here, but I want to show you some very amazing things. Ancient wisdom, the Hermetic tradition tells us that the human body can be regarded as a blueprint for the universe by means of all the ratios that are found within the body. This may indeed be true. Let’s have a look at the following picture:
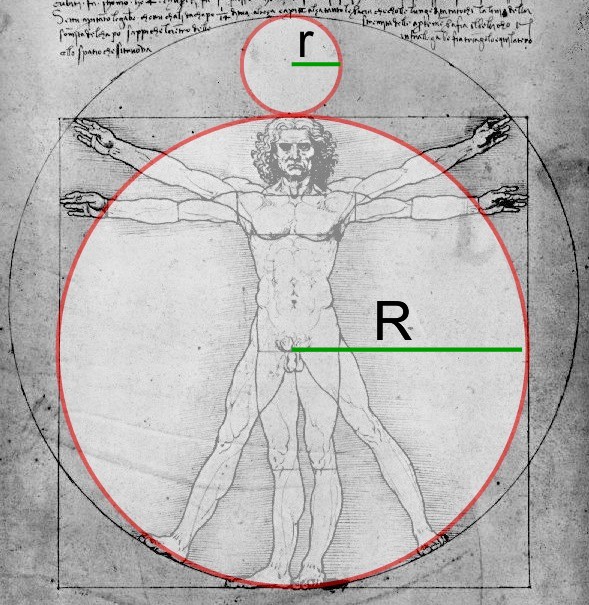
This is the same picture as above, in the picture there are now two red circles added. The biggest red circle fits perfectly and is inscribed by the square. The smaller red circle’s is centered between the outer circle and the inner red circle and tangentially touches both.
Much to our surprise, the upper red circle represents the moon and the lower red circle represents the Earth! In mathematical terms: The ratio of the diameter of the smaller red circle to the bigger red circle r / R equals the ratio of the diameter of the moon to the diameter of the Earth! Now let’s prove it:
(3)
Radius of the moon : r
Radius of the Earth : R
Side of the square is : 2R
The perimeter of the square is : 8 R
Radius of the outer circle is : r + R
The circumference of the outer circle is : 2 p ( r + R )
Now ‘squaring the circle’ makes the perimeter of the square equal to the circle:
8 R = 2 p ( r + R ) 
8 R - 2 p R = 2 p r 
R (8 – 2 p) = 2 p r 
r / R = (8 – 2 p) / 2 p = (4 – p) / p
Earth radius = 6,370,973 m
Moon radius = 1,738,000 m
Moon to Earth ratio = r / R = 0.27279977
r / R = (4 – p) / p = 0.273239544 (p = 3.14159265)
Quod Erat Demonstrandum!
There is another mysterious relation to be discovered in the sketch of the Vitruvian man by Leonardo Da Vinci. The Great Pyramid at the Giza plateau in Egypt called after the pharaoh that is supposedly buried there named Khufu (Cheops in Greek), holds a perfect geometrical relation to the squaring of the circle and the Vitruvian man as depicted by Leonardo Da Vinci!
Look at the picture below:
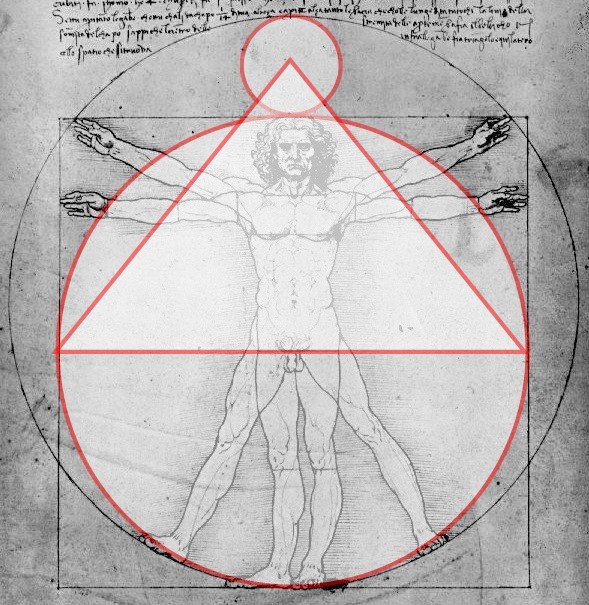
Great Piramid at Giza in relation to Vitruvius man
The triangle in the picture is the exact geometrical proportion of the Great Pyramid at the Giza Plateau near Cairo, Egypt. The angles between the base and the apex (top) of the pyramid are exactly 51 degrees and 51 seconds. (51º 51’).
(4)
The Great Pyramid and in fact the complete layout of the Giza plateau with all its pyramids, sacred temples and the sphinx contains a lot of hidden sacred geometry of which we will reveal more in this book. The point I want to make here is that the Egyptians were aware of the art of sacred geometry and how it relates to the universe, as the Giza plateau and in particular the Great Pyramid proves.
Let there be light
While explaining the Genesis pattern of sacred geometry we mentioned that on the second day of creation God created the Vesica Pisces and that the Vesica Pisces is the geometry of the light particle the photon. The Holy Bible mentions the second day of creation as the creation of the light. By the way did you notice that the Vesica Pisces has the shape of the eye?
It was discovered by Buckminster Fuller, who did a lot of the groundwork in re-establishing sacred geometry, that the geometry of the photon must be two tetrahedrons joined at a common face.
Now the geometrical shape of the double tetrahedron is perfectly circumscribed by the Vesica Pisces whereas the vertices of the tetrahedrons neatly touch the face of the Vesica Pisces. This has been confirmed by Drunvalo Melchizedek another sacred geometry architect!
(5)
The tetrahedron is also the hidden geometry in the electromagnetic wave (wave form of light) itself. The electrical and magnetic fields are perpendicular to each other and a spiral can be drawn connecting the electrical field with the magnetic field that exactly traces over a tetrahedron!
Tom Bearden, the inventor of the MEG machine has proof that James Clerk Maxwell must have known this but that Oliver Heaviside removed the knowledge of the hidden tetrahedron in the simplified version of electrodynamics.
(6)
Notre-Dame de Chartres
The knowledge of sacred geometry has been preserved in the architecture of churches and cathedrals all over Europe. The cathedral of Chartres is famous for its sacred geometry that was used in its design. Sacred geometry can be found for example in the layout of the ground plan and the stained glass windows that contain the Phi ratio.
|

|
|

|
West rose window of the Chartres Cathedral and ground plan
|
http://www.soulsofdistortion.nl/SODA_chapter5.html
|
|
|
|
|
|
|
Numbers Don’t Lie – Ancient Metrology
January 20, 2013

Numbers Don’t Lie – Ancient Metrology
There is an underlying order in Cosmos. Our ancestors discovered it in ancient times and expressed it in their writings and monuments. This article is an invitation to all our visitor to explore and expand this subject. Please share facts that should be mentioned here (via comments and/or e-mail) - if you are aware of them. For example, many people today do not understand that ancient units of measure reflect advanced knowledge of mathematics and astronomy…
1,000 x 360 x 365.24
The result of multiplying above numbers is: 131,486,400
Equatorial Circumference of the Earth: 40,077km= 131,486,400 feet
The official value for equatorial circumference of the Earth: 40,075 kilometers. It reveals connection of the year ( 365.24 days) and the foot (unit of measuring length) with circumference of the Earth.
That is truly a “cosmic” coincidence !!!
“Philosophy is written in this grand book – I mean the universe — which stands continually open to our gaze. But it cannot be understood unless one first learns to comprehend the language and interpret the characters in which it is written. It is written in the language of mathematics, and its characters are triangles, circles, and other geometric figures, without which it is humanly impossible to understand a single word of it.” — Galileo Galilei, Il Saggiatore (1623)
In order to reveal the “language” of the universe, we will explore numbers known by the ancients and compare them with numbers established by modern astronomy, geodesy and metrology (the science of measurement – do not confuse it with meteorology dealing with weather). It is important to realize that units of measure we use today are connected with the size and movements of our planet.
The same applies to the ancient units of measure.
Content:
Units of Measure and Earth | Ancient Units of Length and Time
Astronomy and Calendars
Cosmic Harmony | Laws Written in Stone
Units of Measure and Earth
Geometry (Ancient Greek: geo- “earth“, -metron “measurement“) was originally dealing with measuring of the earth. In our article “How ancient astronomers could have establish dimensions of the Earth?” we presented a simple method of establishing circumference (and diameter) of the earth that (most likely) was used by the ancient astronomers.
Measurement means the act of measuring or the size of something.
|
|
To Measure means to ascertain the dimensions, capacity, or amount (quantity) of something.
A unit of measurement is a definite magnitude of a physical quantity, defined and adopted by convention and/or by law, that is used as a standard for measurement of the same physical quantity. Any other value of the physical quantity can be expressed as a simple multiple of the unit of measurement.
People have always found it necessary to measure time, distance, area, volume and weight, and have devised units that measure these quantities. For time, there is an absolute standard in the motions of the heavens, but for the other quantities the units have had to be chosen arbitrarily.
Official view is that only recently have we succeeded in creating system of measurement accepted all over the world as the standard system for use in science and trade: The International System of Units (SI). However some researchers suggest that in ancient times people were commonly using units of measure related to dimensions of our planet and similar in value ( closely related to each other.)
|
It is important to notice that units of measure we use today are connected with the size and movements of our planet.
The same applies to the ancient units of measure.

Units of Length
Meter
Originally, the meter was designed to be one ten-millionth (1/10,000,000) of a quadrant, the distance between the Equator and the North Pole. In other words, meter was defined as 1/10,000,000 of the distance from the Earth’s equator to the North Pole measured on the circumference through Paris. Using this unit, the circumference of perfectly round Earth should be exactly 40,000, 000 meters (or 40,000 km).
Today, official value of the Earth’s circumference along the line of longitude is 40,007.86 km.

Nautical Mile
A nautical mile ( 1.852 km ) is based on the circumference of Earth. If you divide circumference of the Earth into 360 degrees and then divide each degree into 60 minutes you will get 21,600 minutes of arc.
1 nautical mile is defined as 1 minute of arc (of the circumference of Earth) is This unit of measurement is used by all nations for air and sea travel. Using 40,007.86 km as the official circumference of our planet we get value of the nautical mile in kilometers: 1.852 km (40,007.86/21,600 )
The metric system
The metric system, originating in the French Revolution and propagated widely in the 19th century, has brought a dreary but convenient uniformity to units of measurement. A number of metric systems of units have evolved since the adoption of the original metric system in France in 1791. The current international standard metric system is the International System of Units (SI). An important feature of modern systems is standardization. Each unit has a universally recognized size. In the establishment of the metric system, the quadrant of the earth was measured and set equal to 10,000,000 meters.
The guiding ideas of the French scientists are well expressed in the introduction to the document presented to the Academy:
The idea to refer all measures to a unit of length taken from nature has appeared to the mathematicians since they learned the existence of such a unit as well as the possibility to establish it: they realized it was the only way to exclude any arbitrariness from the system of measures and to be sure to preserve it unchanged for ever, without any event, except a revolution in the world order, could cast some doubts in it; they felt that such a system did not belong to a single nation and no country could flatter itself by seeing it adopted by all the others.
Actually, if a unit of measure which has already been in use in a country were adopted, it would be difficult to explain to the others the reasons for this preference that were able to balance that spirit of repugnance, if not philosophical at least very natural, that peoples always feel towards an imitation looking like the admission of a sort of inferiority. As a consequence, there would be as many measures as nations.
The International System of Units (abbreviated SI from French), established in 1960, is the modern form of the metric system and is generally a system of units of measurement devised around seven base units and the convenience of the number ten.
The SI, is the world’s most widely used system of measurement, which is used both in everyday commerce and in science. The system has been nearly globally adopted with the United States being the only industrialized nation that does not mainly use the metric system in its commercial and standards activities. The United Kingdom has officially partially adopted metrication, with no intention of replacing customary measures entirely. Canada has adopted it for all legal purposes but imperial/US units are still in use, particularly in the buildings trade.
meter or metre (m) – the metric and SI base unit of distance.
Originally, the meter was designed to be one ten-millionth (1/10,000,000) of a quadrant, the distance between the Equator and the North Pole. In other words, meter was defined as 1/10,000,000 of the distance from the Earth’s equator to the North Pole measured on the circumference through Paris. (The Earth is difficult to measure, and a small error was made in correcting for the flattening caused by the Earth’s rotation. As a result, the meter is too short by a bit less than 0.02%. That’s not bad for a measurement made in the 1790′s.)
For practical reasons, for a long time, the meter was precisely defined as the length of an actual object, a bar kept at the International Bureau of Weights and Measures in Paris.
In recent years, however, the SI base units (with one exception) have been redefined in abstract terms so they can be reproduced to any desired level of accuracy in a well-equipped laboratory.
The 17th General Conference on Weights and Measures in 1983 defined the meter as that “distance that makes the speed of light in a vacuum equal to exactly 299, 792, 458 meters per second”. In other words, ”The metre is the length of the path traveled by light in vacuum during a time interval of 1/299, 792, 458 of a second.” The speed of light in a vacuum, c, is one of the fundamental constants of nature. Since c defines the meter now, experiments made to measure the speed of light are now interpreted as measurements of the meter instead.
The meter is equal to approximately:
1.093 613 3 yards,
3.280 840 feet, or
39.370 079 inches.
Its name comes from the Latin metrum and the Greek metron, both meaning “measure.” The unit is spelled meter in the U.S. and metre in Britain; there are many other spellings in various languages
Ancient Units of Length and Time
Megalithic Yard
When the late Professor Alexander Thom surveyed over a thousand megalithic structures from Northern Scotland through England, Wales and Western France he was amazed to find that they had all been built using the same unit of measurement. Thom dubbed this unit a Megalithic Yard (MY = 2.72 feet = 0.829m) because it was very close in size to an imperial yard, being exactly 2 feet 8.64 inches (82.966 cm). As an engineer he could appreciate the fine accuracy inherent in the MY but he was mystified as to how such a primitive people could have consistently reproduced such a unit across a zone spanning several hundreds of miles. The answer that eluded the late Professor lay not in the rocks, but in the stars.The MY turns out to be much more than an abstract unit such as the modern meter, it is a highly scientific measure repeatedly constructed by empirical means. It is based upon observation of three fundamental factors: the orbit of the Earth around the sun, the spin of the Earth on its axis, and the (constant) mass of the Earth.
[ Source: The Mystery of the Megalithic Yard Revealed ]
Making the Megalithic Yard
In the discussions leading up to the French adoption of the metric system in 1791, the leading candidate for the definition of the new unit of length, the metre, was the seconds pendulum at 45° North latitude. It was advocated by a group led by French politician Talleyrand and mathematician Antoine Nicolas Caritat de Condorcet. This was one of the three final options considered by the French Academy of Sciences committee. However, on March 19, 1791 the committee instead chose to base the metre on the length of the meridian through Paris. A pendulum definition was rejected because of its variability at different locations, and because it defined length by a unit of time.


where T is period of simple pendulum (time of one full swing), L is length of pendulum, and g is local acceleration of gravity ( g = 9.81 m/s2 = 32.2 ft/s2).
From this equation, for
L= 1 meter, the pendulum period is T= 2.006 seconds.
For L= 1 MY = 0.83 m, the pendulum period T= 1.827 seconds
(interestingly 666/1.827 = 364.5 , and for L=1 Royal Egyptian Cubit, period T = 1.45 sec )
Full 200 swings of this pendulum would take 365.4 seconds ( 6.09 minutes or 6 min and 5.4 sec). This is exactly the time period during which the moon (or the sun – since both have the same apparent angular diameter = 0.5 deg) moves by 1.5 degree on the sky (it is equivalent to its 3 diameters).
Here is how to make unit of measure equal 1 megalithic yard ( 1 MY)
Note: this is modification (by A. Sokolowski) of a method originally proposed by Lomas, Knight & Butler.
The apparent movement of the sky (caused by rotation of our planet on its axis) provides an excellent astronomical clock.
The earth is rotating 1 degree per 4 minutes of time (360deg/(24×60)min = 0.25 deg/min).
Since apparent angular moon diameter (= angular sun diameter) = 0.5 degree.
On the day of equinox (daytime = night time) the circle of the moon fits exactly 360 times on its path above the horizon (180 degrees).

If we observe the moon, or a bright star (perhaps with help of simple astrolabe with plumb-line), we can easily measure exactly 6 minutes by waiting for the star (or the moon) to move 1.5 degree on its path (this is the time taken by the moon to move on the sky by its 3 diameters). Pendulum with length (L) equal 1 MY would make exactly 200 full swings in 6 minutes (just like a pendulum 1 m long would swing exactly 180 times in 6 minutes). Alternatively we can observe shadow of an obelisk and measure 6 minutes (using template of a half circle divided into 180 degrees).
|
|
|
|
|
When you see the upper edge of the moon (or a first magnitude star) approaching the first marker on the astrolabe, swing the weight of a pendulum and count the pulses from one extreme and back (full swings) for 6 minutes – until the moon/ star moves 1.5 degree (for the moon it would be its 3 diameters). There are only two factors that effect the swing of a pendulum; the length of the string and gravity – which is determined by the mass of the earth ( if you swing a pendulum faster it will move outwards further but it will not change the number of pulses.)
You need to adjust the length until you get exactly 200 swings during this period of 6 minutes. It is likely to take you several attempts to get the length right so be prepared to do quite a bit of moon/star gazing. To improve accuracy, you can increase the time (and accordingly number of pendulum’s swings).
It is likely that in ancient times, astronomers would keep the rod with 1MY length (once it was established this way) and use the described method for calibration.
One you have the correct length of pendulum, mark the distance from the exact point of suspension to the centre of the weight (it would be best to use a spherical weight for the pendulum). Congratulations, you now have a stick that is exactly one Megalithic Yard long.
1 Megalithic Yard = 2.72 feet = 1 foot + 1RC = 0.82966m
1 m = 3.281 feet | 1 foot = 12 inch = 30.48 cm | 1 inch = 2.254 cm
1 Royal Egyptian Cubit = 20.62 inch = 0.531 m
1 mile = 1,609.344 meters = 1,941 MY = sqrt(44) MY
1 nautical mile = 1.15078 mile = 6,076 feet = 1.852 km = 2233 MY
Modern and accurate numbers describing the size of our planet:
Earth’s Circumference Between the North and South Poles:
21,602.6 nautical miles = 24,859.82 miles (40,008 km)
Earth Equatorial Circumference:
24,901.55 miles (40,075.16 kilometers)
Earth’s Diameter at the Equator:
6,887.7 nautical miles = 7,926.28 miles (12,756.1 km)
1 year = 365.25 days
1 day = 24 hours = 1,440 minutes = 86,400 seconds
24 hours = 360 degrees,
1 hour = 15 degrees,
1 minute (time) = 0.25 degree = 15 min of arc
1 degree = 4 minutes (time)
360 degrees = 21,600 minutes = 1,296,000 seconds (of arc)
1 degree = 60 min = 360 seconds (of arc)
Note:1/1,000th of a degree of arc around the equatorial circumference of the Earth is just 365.22 ft in length!
1 degree of arc = (1/360) * 40,075.16 km = 111.32 km = 365,223 feet (divided by 1000 = 365.22 which is number of days in a year)
Egyptian Cubit
The Egyptian cubit, the Indus Valley units of length referred to above and the Mesopotamian cubit were used in the 3rd millennium BC and are the earliest known units used by ancient peoples to measure length. The measures of length used in ancient India included the dhanus (bow), the krosa (cry, or cow-call) and the yojana (stage).
The Egyptian Royal Cubit rod, from the Turin collection, has an official length of 20.618 inches. Its refined value, under the sexagesimal geodetic system, was calculated mathematically to be 20.61818182 inches.
Note: Royal Cubit consists of 28 units, digits, which is the same as 7 palms of 4 digits. The names of divisions of royal cubit may suggest anatomical origin, however the divisions indicate astronomical origin of the cubit (7 days per week, 28 days lunar calendar, 4 weeks per lunar month)…
Interesting Relationship between ancient units of lengths
From measurements of the King’s chamber and other dimensions in the Great Pyramid by John Greaves, Sir Isaac Newton realized that the King’s Chamber was 10 x 20 Royal Cubits (or Thoth Cubits) so that the Royal Cubit is determined as equal to 1.719 (1.72) feet.
Therefore, we can take the following as “ideal values” in metric system of 3 fundamental ancient units of length:
1MY = 1 foot + 1RC = 2.72 feet = 0.829m
1 Royal Cubit = 1.72 feet = 0.632 MY = 0.524m
1 Remen = Royal Cubit/sqrt(2) = 14.58 inch = 0.37 m
Notice the relationship between all 3 units can be well approximated as follows:
1 Megalithic Yard = sqrt(5) x 1 Remen = 1 Royal Cubit x sqrt(5/2) = 1.5811388 RC
Let’s notice the relationship between all 3 units can be well approximated as follows:
1 Megalithic Yard = sqrt(5) x 1 Remen = 1 Royal Cubit x sqrt(5/2) = 1.5811388 RC
1 Royal Cubit = sqrt(2) x 1 Remen = 0.525 m
1 Megalithic Yard = sqrt(5) x 1 Remen = 0.83 m

It may be seen that, from the basic square side of the Remen, the length of the Royal Cubit can be derived by multiplying the Remen by the square root of 2; similarly, the Megalithic yard can be derived by multiplying the Remen by the square root of 5.
Another geometric illustration of the relationship between Remen, Royal Cubit and Megalithic Yard, where1M.Y. is circumference of the circle (0.823m) inscribed in (1/2) R.C. square (with 99.3 % accuracy):

If Megalithic Yard was defined as equal to the circumference of the circle inscribed in ½ of Royal Cubit square:
1 MY=1/2 x RC x “Pi” so 1 MY = 1.570795 RC
1 MY (in RC) = Pi/2

For RC=1 we get and 1MY=1.570795 and 1 Remen = 1/sqrt(2)=0.7071
NOTE:
For the Great Pyramid:
Height = 280 Royal Cubits
Base Side = 440 Royal Cubits = 280 MY
 Click to Enlarge Click to Enlarge
In whichever case, the Greeks and Romans inherited the foot from the Egyptians.
12 inches = 1 foot
36 inches = 3 feet = 1 yard
1760 yards = 1 mile
440 yards = quarter mile
Interest in ancient metrology was triggered by research into the various Megalith building cultures and the Great Pyramid of Giza.
In 1637 John Greaves, professor of geometry at Gresham College, made his first of several studies in Egypt and Italy, making numerous measurements of buildings and monuments, including the Great Pyramid. These activities fueled many centuries of interest in metrology of the ancient cultures by the likes of Isaac Newton and the French Academy. |
|
|
|
|
The first known description and practical use of a physical pendulum is by Galileo Galilei, however, Flinders Petrie, a disciple of Charles Piazzi Smyth, is of the opinion that it was used earlier by the ancient Egyptians. Writing in an article in Nature, 1933 Petrie says:
If we take the natural standard of one day divided by 105, the pendulum would be 29.157 inches (0.7405878 m) at lat 30 degrees. Now this is exactly the basis of Egyptian land measures, most precisely known through the diagonal of that squared, being the Egyptian double cubit. The value for this cubit is 20.617 inches, while the best examples in stone are 20.620±0.005inches.
By the time measurements of Mesopotamia were discovered, by doing various exercises of mathematics on the definitions of the major ancient measurement systems, various people (Jean-Adolphe Decourdemanche in 1909, August Oxé in 1942) came to the conclusion that the relationship between them was well planned.
Livio C. Stecchini claims in his A History of Measures:
The relation among the units of length can be explained by the ratio 15:16:17:18 among the four fundamental feet and cubits. Before I arrived at this discovery, Decourdemanche and Oxé discovered that the cubes of those units are related according to the conventional specific gravities of oil, water, wheat and barley.
Stecchini makes claims that imply that the Egyptian measures of length, originating from at least the 3rd millennium BC, were directly derived from the circumference of the earth with an amazing accuracy. According to “Secrets of the Great Pyramid” (p. 346), his claim is that the Egyptian measurement was equal to 40,075,000 meters, which compared to the International Spheroid of 40,076,596 meters gives an error of 0.004%. No consideration seems to be made to the question of, on purely technical and procedural grounds, how the early Egyptians, in defining their cubit, could have achieved a degree of accuracy that to our current knowledge can only be achieved with very sophisticated equipment and techniques.
Alexander Thom
Oxford engineering professor Alexander Thom, doing statistical analysis of survey data taken from over 250 stone circles in England and Scotland, came to the conclusion that there must have been a common unit of measure which he called a megalithic yard. This research was published in the Journal of the Royal Statistical Society (Series A (General), 1955, Vol 118 Part III p275-295) as a paper entitled A Statistical Examination of the Megalithic Sites in Britain.
As Professor Thom observed in his book Megalithic Sites in Britain (1967):
“It is remarkable that one thousand years before the earliest mathematicians of classical Greece, people in these islands not only had a practical knowledge of geometry and were capable of setting out elaborate geometrical designs but could also set out ellipses based on the Pythagorean triangles.”
Robin Heath
Later, these ideas were further developed as defense for the Imperial units against the emerging metric system, and adopted by parts of the anti-metric movement. Robin Heath, in his book Sun, Moon & Stonehenge, connects the megalithic yard (and thus Stonehenge) to the imperial foot, and manages to connect a few astronomical phenomena, and the Egyptian Royal Cubit (and thus the Great Pyramid) into one grand equation (MY is an abbreviation for megalithic yard):
If the lunar year is represented by 12 MY then 1 ft corresponds precisely to the extra 10.875 days to coincide with the end of the solar or seasonal year. Furthermore, the period between the end of the solar year and 13 lunations – 18.656 days – is represented by another unit of length from antiquity, the ‘Royal Cubit’ of 20.63 inches or 1.72 ft.
Note: 1 solar year = 365.24 days,
1 lunar year = 12 lunar months = 354.36 days.
(1 lunar month = the time between full moons = 29.530589 days, therefore 1 lunar year = 12 * 29.53 = 354.36 and 365.24 – 354.36 = 10.88.
Therefore
1 solar year = 1 lunar year (12 lunar months) + 10.88 days.
If 1 lunar month is represented by 1 MY we get 29.53 days represented by 2.72 feet (or 10.8566 days are represented by 1 foot).
One lunar year (12 lunar month) = 354.36 days represented by 12 MY = 12* 2.72 feet= 32.64 feet
Also 13 lunar months = 13*29.53 = 383.89 days.
13 lunar months – 1 solar year = 383.89 – 365.24 = 18.65 days (representing 1.718 feet = 1 Royal Cubit).
18.65 /10.8566 = 1,718 feet = 1 Royal Cuibt
This seems to bring pseudo-scientific metrology to new heights, especially in view of the conclusion:
Hence the equally astonishing revelation that 1 MY = 1 ft + 1 RC. Assuming that the MY was the primary unit, then the derivative foot and cubit appear to have formed a logical and essential part of the astronomical and calendrical researches of our Neolithic ancestors. If, however, the foot preceded the MY in time – and here we must remember that 1/1,000th of a degree of arc around the equatorial circumference of the Earth is just 365.244 ft in length! – then knowledge of the roundness of the Earth must have predated use of the MY…i.e. well before 3,000BC. There are no other choices readily apparent!
J. Michell claims that all over the world traditional units of measurements are related.
He goes on to point out the value of the pu that still survives in Indo-China is given in L.D’A. Jackson’s Modern Metrology (available on the net) as 2.7272 miles with the fraction repeating. Without knowledge of the pu’s existence its former use in Britain was deduced by J. F. Neal, who called it the Megalithic Mile because the ratio is similar to that between the foot and the Megalithic Yard.
Since the ratio between the dimensions of the Earth and Moon is 10:2.7272 the following relationships unambiguously exist.
Earth’s diameter = 7,920 miles
Moon’s diameter = 792 megalithic miles
Perimeter of the square containing the circle of the Earth = 31,680 miles
Perimeter of the square containing the circle of the Moon = 3,168 megalithic miles.
Sun’s diameter = 864,000 miles = 316,800 megalithic miles.
More information: http://blog.world-mysteries.com/science/ancient-timekeepers-part-5-units-of-measurement/
Units of Time
Observing movement of the Sun and the stars suggested that Earth is spinning around its own axis and that the Sun is moving against the background of constellations. This suggested there are 2 cycles: earth axis spin cycle and earth around the sun orbital cycle.
In ancient times it was easy to observe the Sun in order to establish units of time so it is good assumption that such units would be “solar units of time”. We use them today and call them “solar days” or simply days (as opposed to stellar background based “sidereal days”). It was also easy to observe the moon and the stars at night.
Hipparchus (190-120 BC) and his predecessors used various instruments for astronomical calculations and observations, such as the gnomon, the astrolabe, and the armillary sphere. Hipparchus is credited with the invention or improvement of several astronomical instruments, which were used for a long time for naked-eye observations. According to Synesius of Ptolemais (4th century) he made the first astrolabion: this may have been an armillary sphere (which Ptolemy however says he constructed, in Almagest V.1); or the predecessor of the planar instrument called astrolabe (also mentioned by Theon of Alexandria). With an astrolabe Hipparchus was the first to be able to measure the geographical latitude and time by observing stars. Previously this was done at daytime by measuring the shadow cast by a gnomon, or with the portable instrument known as a scaphe. [ -- Wikipedia ]
Illustration below shows ancient Egyptians’ interest in astronomy.
 The Northern [Bottom] and Southern [Top] Panel ‘Decan Chart’ from the Tomb of Senmut [c 1500 BC]. [In reality this panel is about 4 m long.] The decan system was actually used as a clock for time keeping in the night hours and through the year – modern Egyptologists call them Egyptian sidereal clocks. The Northern [Bottom] and Southern [Top] Panel ‘Decan Chart’ from the Tomb of Senmut [c 1500 BC]. [In reality this panel is about 4 m long.] The decan system was actually used as a clock for time keeping in the night hours and through the year – modern Egyptologists call them Egyptian sidereal clocks.
After these cycles were noticed (discovered) the next step would be to quantify them (describe them using specific units of measurement).
Numbers like 360, 72, 30, 12 and multiples thereof were intentionally plotted in ancient myths. It was as if the storyteller were trying to convey a secret code. Here’s what the figures signify in the precession cycle:
- 360 degrees = 12 x 30 degrees, or one full circuit through the zodiac constellations
- 72 years = the time it takes for the stars to shift 1 degree
- 30 degrees = one astrological age (a different zodiac constellation rises with the Sun every 2,160 years)
- 12 = the total number of zodiac signs or astrological ages. 12 times 2,160 = 25,920 years, or one full precession cycle
- In Babylonia, the ancient scribe Berossus wrote that mythical kings ruled before the Great Flood for a total 432,000 years.
- In India, the Rigvida contains exactly 432,000 syllables. And although the calculation has created some confusion of late, the Vedic Kali Yuga (representing the current world age) is said to be comprised of 432,000 years.
- On the other side of the globe, Mayan calendar units parrot the precessional figures.
For example: 1 tun (an astronomical year) = 360 days;
6 tuns = 2,160 days;
1 katun = 7200 days,
6 katuns = 43,200.
The standard Mayan base of 20 (ours is 10) is arrived at by dividing 43,200 by 2,160.
|
|
|
|
|
Today we use decimal system (multiples of 10) however when it comes to measuring angles, we use ancient convention: a circle is not divided into 100 (or 1000 parts), instead it divided in 360 units (called degrees) and each unit is further divided into 60 equal pats called minutes and each one of these is further divided into 60 equal units called seconds.
A full circle has 360 degrees, 21,600 (360×60) minutes and 1,296,000 (360x60x60) seconds.
Ancient divided the whole sky into 12 equal parts called constellations.
- Zodiac (circle division): 12 equal parts (or 4×3): 4 quarters each into 3 and further each third into 10 (4, 3, 10)
- Each Constellation had 30 degrees (360/12)
- 30 degrees = 1,800 minutes = 108,000 seconds.
Dividing the daily cycle into equal parts established units of time.
Ancient divisions were not decimal but based on 24 and 60:
1/24 of the Earth spin cycle was unit we call now 1 hour, Each hour is divided into 60 equal units (called minutes) and each minute is divided into 60 equal units (called seconds).
The finest unit of time in ancient times was one second:
1/(24x60x60) = 1/86400 part of one spin cycle (1 day). In other words 1 rotation cycle of the Earth (one day) has 24 hours, 1,440 minutes and 86,400 seconds.
Each day was divided into 24 parts called hours, each hour into 60 minutes and each minute in to 60 seconds (today we divide seconds using decimal system; 1/10, 1/100, 1/1000 (millisecond).
Each day has 24 hours = 1440 minutes (24×60) = 86,400 seconds (24x60x60).
The Earth turns 15 degrees per hour (1 degree each 4 minutes).
Astronomy and Calendars
All calendars began with people recording time by using natural cycles: days, lunar cycles (months), and solar cycles (years). Ancient peoples have attempted to organize these cycles into calendars to keep track of time and to be able to predict future events of importance to them, such as seasons (e.g. the annual Nile flood in ancient Egypt), eclipses etc. The main problem was that these natural cycles did not divide evenly.
Early people could either try to stay in sync with the moon, perhaps making months alternating combinations of 29 and 30 days, with special rules to re-sync occasionally with a solar year by adding leap months (such as the Jewish or Chinese calendar) or abandon lunar cycles and concentrate on the solar year (such as the Ancient Egyptian calendar of 12 same-sized months).
Today, the solar year is 365.242199 days long (or 365 days 5 hours 48 minutes 46 seconds) and the time between full moons is 29.530589 days.
Therefore in 1 year there are 12.37 moon cycles (365.24 / 29.53 = 12.37).
The Moon makes a complete orbit around the Earth with respect to the fixed stars about once every 27.3 days (sidereal period). However, since the Earth is moving in its orbit about the Sun at the same time, it takes slightly longer for the Moon to show the same phase to Earth, which is about 29.5 days (its synodic period).
Nature’s Nearly Perfect Calendar
The Moon could be “Nature’s perfect clock” if the solar cycle period were exactly divisible by the period of the lunar cycle.
For example if the solar year were exactly 364 days (instead of 365.24 ) and lunar cycle exactly 28 days (instead of 29.53), we would have a “perfect calendar” based on 13 months of 28 days per month, with each month having 4 weeks of 7 days. Such calendar was proposed as “13 Moon Calendar” (discussed later in this article) with the 365th day called the “Day Out of Time”.
Another “perfect calendar” would require solar year to have 360 days and lunar cycle 30 days:
- The “perfect” Earth would take 360 days to complete 360 degree circular solar orbit (1 deg per day).
- The “perfect” Moon would take 30 days to complete 360 degree circular orbit around the Earth (12 deg per day).
- In such case, we could have a year based on 12 months of 30 days. Each month would have 5 weeks of 6 days each.
We can only wonder if these numbers were true for the Earth in the the early period of the solar system…
13 Moon Calendar
A Culture of Peace through a Calendar of Peace
The 13 Moon Natural Time Calendar is based upon Dreamspell – a universal application of the mathematics and cosmology of the Classic Mayan Calendar and Prophecy of 2012 as deciphered and presented by Jose and Lloydine Arguelles.
Around the world, people of diverse beliefs and cultures are unifying with the 13 moon calendar as a global harmonic standard – thirteen moons of 28 days, with one day to celebrate “Peace Through Culture” before each new year (July 26).
Introduction to the 13 Moon Calendar:
The Thirteen Moon/28 day calendar is a perpetual, harmonic calendar. It is called a Moon Calendar because it is based on the female 28-day (average) menstruation cycle, which is also the average lunar cycle. The measure of the moon from new moon to new moon is called the synodic cycle and is 29.5 days in length.
However, the sidereal lunar cycle which measures the moon from where it reappears in the same place in the sky is only 27.1 days in length. So 28 days is the average lunar cycle.
In actuality the moon goes around the Earth thirteen times a year. This means that the 13 Moon calendar is a genuine solar-lunar calendar which measures the Earth’s orbit around the sun by the lunar average of 28 days.
Thirteen perfect months of 28 days = 52 perfect weeks of 7 days = 364 days.
The 365th day is called the “Day Out of Time” because it is no day of the week or month at all. This day which falls on the Gregorian correlate date of July 25 is a day for forgiveness and for the artistic celebration of life and freedom.
The synchronization, or new year’s date of the 13 Moon calendar is July 26. This corresponds to the rising of the great star Sirius. This makes the 13 Moon Calendar a tool for harmonizing ourselves with the galaxy.
Perfect Periodicity
For every one time we go around the Sun,the Moon goes around Earth 13 times.
The year has already been divided by Nature-13 ‘moon’ths of perpetual harmony.
Related Links
Cosmic Harmony
Earth Facts
Revolution Period around Sun: 365.2425 days
Rotation on Axis: 23 hours and 56 minutes and 04.09053 seconds.
Note: it takes an additional four minutes for the earth to revolve to the same position as the day before relative to the sun (i.e. 24 hours).
Axial Tilt: 23.4 o (23°26’21.4119″)
 Earth’s Circumference at the Equator: Earth’s Circumference at the Equator:
21,638.855 nautical miles = 24,901.55 miles (40,075.16 km)
Earth’s Circumference Between
the North and South Poles:
21,602.6 nautical miles = 24,859.82 miles (40,008 km)
Earth’s Diameter at the Equator:
6,887.7 nautical miles = 7,926.28 miles (12,756.1 km)
Equatorial Radius (1/2 of the diameter):
3,443.9 nautical miles = 3,963.14 miles (6,378.05 km)
Earth’s Diameter at the Poles:
7,899.80 miles (12,713.5 km)
Polar Radius: 3,950 miles (6,356.75km)
Average Distance from the Earth to the Sun:
93,020,000 miles (149,669,180 km)
Average Distance from the Earth to the Moon:
238,857 miles (384,403.1 km)

The closest distance between Earth and Sun is 147 x 106 km, which converted to Royal Egyptian Cubits is 280 x 109 ( 280 cubits is the height of the Great Pyramid).
Observe the measurements of the Moon:
Equatorial radius 1,738.14 km (0.273 Earths) so
the Moon Diameter is: 3,476.28 km or 2,160 miles.
Let’s make this “the cosmic unit” (one moon unit)
representing the “ideal” diameter of The Moon.
Diameter of The Sun =865,294 miles*.
If we divide 865,294 by 2,160 astonishingly
we get 400.6 …
|
|
|
 Primer Primer
 Anterior
70 a 84 de 159
Siguiente Anterior
70 a 84 de 159
Siguiente Último
Último
|
|
| |
|
|
©2024 - Gabitos - Todos los derechos reservados | |
|
|

