|
|
General: VESICA PISCIS=JUAN 21:11="AGUJERO DE GUSANO ALQUIMICO A NIVEL MUNDIAL"=BEBE
Choose another message board |
|
Reply |
Message 1 of 6 on the subject |
|
TABERNACULO =TEMPLO DE SALOMON = KAABA = GIZE= VATICANO= WASHINGTON D.C = NUEVA JERUSALEN = JUAN MARCOS
CENACULO DE JERUSALEN=SAN MARCOS
"AGUJERO DE GUSANO MUNDIAL" ES VESICA PISCIS. NEXO CON EL CUBO
En diversos periodos de la historia ha sido tema de especulaciones místicas; probablemente los primeros fueron los Pitagóricos, que la consideraban una figura sagrada. La razón matemática de su anchura (medida por los puntos extremos del "cuerpo", sin incluir la "cola") por su altura fue aproximada por el cociente 265:153. Esta razón, que da 1,73203, se consideró un número sagrado llamado la medida del pez. Exactamente, la razón geométrica de estas dimensiones es la raíz cuadrada de 3, o 1,73205... (ya que si se traza la línea recta que une los centros de ambos círculos, junto con los dos puntos donde los círculos se intersecan, se obtienen dos triángulos equiláteros unidos por un lado). El cociente 265:153 es una aproximación a la raíz cuadrada de 3, y tiene la propiedad de que no se puede obtener ninguna aproximación mejor con números más pequeños. El número 153 aparece en el Evangelio de Juan (21:11) como el número de peces que Jesús hizo que se capturaran en la milagrosa captura de los peces, lo que algunos consideran como una referencia cifrada de las creencias pitagóricas.

APOCALIPSIS 21
NU-EVA J-ER-U-S-A-LE-N /JUAN
EVA (NUMERO NU-EVE)=MARIA MAGDALENA O MARIA LA GRANDE
JUAN MARCOS=SANTO GRIAL
9. Vino entonces a mí uno de los siete ángeles que tenían las siete copas llenas de las siete plagas postreras, y habló conmigo, diciendo: Ven acá, yo te mostraré la desposada, la esposa del Cordero. (Noten la relacion de la COPA CON LA ESPOSA DEL CORDERO)
10. Y me llevó en el Espíritu a un monte grande y alto, y me mostró la gran ciudad santa de Jerusalén, que descendía del cielo, de Dios,
11. teniendo la gloria de Dios. Y su fulgor era semejante al de una piedra preciosísima, como piedra de jaspe, diáfana como el cristal. (LA "GLORIA DE DIOS" es una clave sabatica en contexto a EXODO 24 Y 25. Se vuelve a repetir el patron del libro de EFESO EN SU CAPITULO 5.)
12. Tenía un muro grande y alto con doce puertas; y en las puertas, doce ángeles, y nombres inscritos, que son los de las doce tribus de los hijos de Israel;
13. al oriente tres puertas; al norte tres puertas; al sur tres puertas; al occidente tres puertas.
14. Y el muro de la ciudad tenía doce cimientos, y sobre ellos los doce nombres de los doce apóstoles del Cordero.
ESTRELLA DE DAVID ES LA ALQUIMIA, OSEA LA UNION ENTRE EL HOMBRE Y LA MUJER
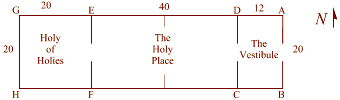
(ABCD) Double Square in Solomons Temple
EL LUGAR SANTISIMO DEL TABERNACULO Y DEL TEMPLO DE SALOMON TENIA FORMA DE CUBO
NOTEN LA ESTRELLA DE 5 PUNTAS EN EL CENTRO DEL EXAGONO CENTRO DE LA ESTRELLA DE 6 PUNTAS
EL EXAGONO TAMBIEN ES UNA REFERENCIA AL CUBO.
NOTEN QUE EN ESTA ESTRELLA DE 6 PUNTAS HAY 13 TRIANGULOS DE 5 PUNTAS, OSEA QUE NOS DA UN NEXO CON LAS 12 CONSTELACIONES DEL ZODIACO, CON LAS 12 HORAS DEL DIA, CON LAS 12 LUNAS QUE HAY EN EL CALENDARIO, CON LA SANTA CENA EN EL CONTEXTO A LOS 12 APOSTOLES, CON LAS 12 TRIBUS DE ISRAEL, CON EL MERIDIANO DE GREENWICH E INCLUSO CON ROSE LINE, ETC,ETC. TODO TIENE COMO PATRON LA ESTRELLA DE 6 PUNTAS, OSEA LA UNION ENTRE EL HOMBRE Y LA MUJER QUE LA TRADICION RELIGIOSA "OLVIDO". ESTE ES EL PATRON ESOTERICO DETRAS DE APOCALIPSIS 22 EN SU RELACION CON VENUS.

Noten el MONSTRUOSO NUMERO 36, incluso con la FORMA DE ORION, en una estrella de 6 puntas. Son siete pelotitas, con 6 perimetrales. 6x6=36
AQUI ESTA EL ULTRA SECRETO DEL NEXO 666 CON LA PIRAMIDE DE LOUVRE, EN EL CODIGO DA VINCI. 1+2+3+ 4+5+6+7+8+9 +20+11+12+13 +14+15+16+17+18 +19+20+21+22+23 +24+25+ 26+27+28+29 +30+31 +32+33+ 34+35 +36=666

15. El que hablaba conmigo tenía una caña de medir, de oro, para medir la ciudad, sus puertas y su muro.
16. La ciudad se halla establecida en cuadro, y su longitud es igual a su anchura; y él midió la ciudad con la caña, doce mil estadios; la longitud, la altura y la anchura de ella son iguales. (LA CUBICACION DE UNA ESFERA. HAY UN OBVIO NEXO ALQUIMICO. LA GRAN CIUDAD ESTA DISEÑADA CON EL MISMO PATRON DE LA GRAN PIRAMIDE DE GIZE)

Figura 16. La relación geométrica entre el codo real y el metro.
LA CLAVE MATEMATICA ESTA EN LA ECUACION:
PI-(PHI ELEVADO AL CUADRADO)=CODO REAL
 |
|
3.1416 - 2.61800 = 0.5236
|
3.1416-2.618=0.5236
CODO REAL=.5236
ESTE ES EL SECRETO DEL NEXO "ROSE LINE", EN EL CONTEXTO AL METRO Y EN EL CONTEXTO A LA PIRAMIDE DE LOUVRE.
17. Y midió su muro, ciento cuarenta y cuatro codos, de medida de hombre, la cual es de ángel.
21. Las doce puertas eran doce perlas; cada una de las puertas era una perla. Y la calle de la ciudad era de oro puro, transparente como vidrio.
22. Y no vi en ella templo; porque el Señor Dios Todopoderoso es el templo de ella, y el Cordero.
23. La ciudad no tiene necesidad de sol ni de luna que brillen en ella; porque la gloria de Dios la ilumina, y el Cordero es su lumbrera.


Haz clic en la imagen para volver
INICIACIÓN A LOS NÚMEROS DE LA ARQUITECTURA O DE COMO DARLE FORMA A UN EDIFICIO
Los números pueden estar explicados matemáticamente en la “red” pero el problema que plantea el conocimiento de la arquitectura es: ¿cómo se le da forma con esos números a un edificio?. En arquitectura los números operan a partir de los polígonos estrellados formando concatenaciones, tal y como a continuación vamos a describir.

NÚMERO DE ORO - PENTÁGONO
El número de oro viene dado por la solución a la ecuación de segundo grado
x + x² = 1 x = 1+√5 /2 = 1,618033989
Propiedades 1/ 1,618 = 0,618 1,618... x 1,618... = 2,618...
Dado una circunferencia de radio 1 el lado del decágono inscrito en él es 0,618...
Dado un pentágono de lado 1, las diagonales de ese pentágono = 1,618...
La técnica con la que opera la arquitectura es la de las concatenaciones.
Una de ellas, la más usual, es la que presentamos en el dibujo. Si la circunferencia en color azul tiene R=1 el radio de la roja es R= 2,618, correspondiente a la que presentamos en “El vitruvio” de Leonardo da Vinci en la portada de este trabajo.
Se aplicará en la restitución de una tabla de F. Brunelleschi Nº 6.
 
NÚMERO DE PLATA - EL OCTÓGONO
Así como el número de oro está asociado a la √5 el número de plata está asociado a √2 y presenta una serie de propiedades similares a las del número de oro.
√2 = 1,414213562 tg. 22,5º = 0,414213562
tg.67,5º = 2,414213562
1/2,4142... = 0,4142... 2,4142... x 1,4142... = 3,4142...
Observa nuevamente la concatenación, esta vez con el octógono, de la circunferencia en color azul sobre la de color rojo.
Si el radio de la circunferencia azul es 1 la de color rojo es 2,4142....
Si el radio de la circunferencia azul es 0,4142... la de rojo es 1.
Aquí tenéis un ejemplo.
Se aplicará en la Rix House de J. Soane Nº 3.
NÚMERO DE PLATINO - EL HEXÁGONO
De igual forma que el número de oro está relacionado con la √5 y el de plata con la √2, el de platino lo va a estar con la √3
√3 = tg.60º = 1,732050808
1,732... x 2,732... = 4,732...
Combinación, esta, muy utilizada por Andrea Palladio.
Observa la concatenación de la circunferencia azul sobre la de rojo, a través del hexágono, directamente a la circunferencia azul. Si el radio de la circunferencia color azul es 1 el de la circunferencia en color rojo es 2 y el lado del triángulo inscrito es 2 x 1,732...
Este polígono es el más prolífico en la historia de arquitectura como vamos a verlo en los ejercicios.
Aquí tenéis un ejemplo.
Se aplicará al resto de los trabajos Nº 1 - 2 - 4 y 5.
Todos los derechos reservados. Depósito Legal ZA - Nº 69 - 1998
Página web optimizada para ver en resolución de 1024 x 768
2006 - 2007
|
|
|
 First
First
 Previous
2 to 6 of 6
Next
Previous
2 to 6 of 6
Next
 Last
Last

|
|
Reply |
Message 2 of 6 on the subject |
|
NUMERO 153/ VESICA PISCIS / DISEÑO DEL OJO EN FUNCION AL NUMERO 153/ GRAN PIRAMIDE /WASHINGTON D.C / JUAN 21:11 (SEÑAL DE JONAS) / QUINTO DIA JUEVES ( CREACION DE LOS PECES Y LAS AVES, SEGUN GENESIS 1:20) /JUPITER /


IN GOD WE TRUST
NOSOTROS CREEMOS EN DIOS
EL 1 DE MAYO DE 1776=1/5/1+7+7+6=21=2+1=3 OSEA 1/5/3
"porque, cuando Jonás estaba en la barriga del pez tres días y tres noches, así el Hijo de Hombre estará en el corazón de la tierra tres días y tres noches".
- Mateo12:40

|
|
|
|
Reply |
Message 3 of 6 on the subject |
|
|
|
|
Reply |
Message 4 of 6 on the subject |
|
Agujero de gusano
GUSANO/ USA / JERUSALEN
De Wikipedia, la enciclopedia libre

Esquema de un agujero de gusano que permite técnicamente el viaje a través del tiempo. Si uno de los dos extremos del puente atravesado por la línea verde está en movimiento, seguir la ruta roja y volver al punto inicial según el sentido opuesto a la ruta verde podría permitir volver atrás en el tiempo, ya que el espacio-tiempo representado contendría curvas temporales cerradas.
En física, un agujero de gusano, también conocido como puente de Einstein-Rosen y en algunas traducciones españolas «agujero de lombriz», es una hipotética característica topológica de un espacio-tiempo, descrita por las ecuaciones de la relatividad general, consistente esencialmente en un «atajo» a través del espacio y el tiempo. Un agujero de gusano tiene por lo menos dos extremos, conectados a una única «garganta», pudiendo la materia 'desplazarse' de un extremo a otro pasando a través de ésta. Hasta la fecha no se ha encontrado ninguna evidencia de que el espacio-tiempo conocido contenga estructuras de este tipo, por lo que en la actualidad es sólo una posibilidad teórica.
Cuando una estrella supergigante roja explota, arroja materia hacia el exterior, por lo que acaba teniendo un tamaño inferior y acaba convertida en una estrella de neutrones. Pero también puede suceder que se comprima tanto que absorba su energía hacia dentro y desaparezca dejando un agujero negro en el lugar que ocupaba. Este agujero tiene una gravedad tan grande que ni siquiera la radiación electromagnética puede escapar de su interior. El agujero está rodeado por una frontera esférica, llamada horizonte de sucesos. La luz traspasa esta frontera para entrar, pero no puede salir, por lo que el agujero visto desde grandes distancias debería ser completamente negro (aunque Stephen Hawking postuló que ciertos efectos cuánticos generarían la llamada radiación de Hawking). Dentro del agujero los astrofísicos conjeturan que se forma una especie de cono sin fondo. En el año de 1994, el Telescopio espacial Hubble detectó la presencia de uno muy denso en el centro de la Galaxia elíptica M87, pues la alta aceleración de gases en esa región indica que debe haber un objeto 3.500 millones de veces más masivo que el Sol. Finalmente, este agujero terminará por absorber a la galaxia entera.[1]
El primer científico en advertir de la existencia de agujeros de gusano fue Ludwig Flamm en 1916. En este sentido la hipótesis del agujero de gusano es una actualización de la decimonónica teoría de una cuarta dimensión espacial que suponía -por ejemplo-, dado un cuerpo toroidal en el que se podían encontrar las tres dimensiones espaciales comúnmente perceptibles, una cuarta dimensión espacial que abreviara las distancias, y así los tiempos de viaje. Esta noción inicial fue plasmada más científicamente en 1921 por el matemático Hermann Weyl en conexión con sus análisis de la masa en términos de la energía de un campo electromagnético[2] a partir de la teoría relativista de Albert Einstein publicada en 1916.
En la actualidad la teoría de cuerdas admite la existencia de más de tres dimensiones espaciales (ver hiperespacio), pero las otras dimensiones espaciales estarían contractadas o compactadas a escalas subatómicas (según la teoría de Kaluza-Klein), por lo que parece muy difícil (diríase "imposible") aprovechar tales dimensiones espaciales «extras» para viajes en el espacio y en el tiempo.
Origen del nombre[editar]
El término «agujero de gusano» fue introducido por el físico teórico estadounidense John Wheeler en 1957 y proviene de la siguiente analogía, usada para explicar el fenómeno: imagine que el universo es la piel de una manzana, y un gusano viaja sobre su superficie. La distancia desde un lado de la manzana hasta el otro es igual a la mitad de la circunferencia de la manzana si el gusano permanece sobre la superficie de ésta. Pero si en vez de esto, cavara un agujero directamente a través de la manzana la distancia que tendría que recorrer sería considerablemente menor, recordando la afirmación que dice «la distancia más cercana entre dos puntos es una línea recta que los une a ambos».
Tipos de agujeros de gusano[editar]
- Los agujeros de gusano del intra-universo conectan una posición de un universo con otra posición del mismo universo en un tiempo diferente. Un agujero de gusano debería poder conectar posiciones distantes en el universo por plegamientos espaciotemporales, permitiendo viajar entre ellas en menor tiempo del que tomaría hacer el viaje a través de espacio normal.
- Los agujeros de gusano del inter-universo asocian un universo con otro diferente y son denominados «agujeros de gusano de Schwarzschild». Esto nos permite especular si tales agujeros de gusano podrían usarse para viajar de un universo a otro paralelo. Otra aplicación de un agujero de gusano podría ser el viaje en el tiempo. En ese caso sería un atajo para desplazarse de un punto espaciotemporal a otro diferente. En la teoría de cuerdas un agujero de gusano es visualizado como la conexión entre dos D-branas, donde las bocas están asociadas a las branas y conectadas por un tubo de flujo. Se cree que los agujeros de gusano son una parte de la espuma cuántica o espaciotemporal.
Otra clasificación:
De momento existen teóricamente diferentes tipos de agujeros de gusano que son principalmente soluciones matemáticas a la cuestión:
- El supuestamente formado por un agujero negro de Schwarzschild; este «agujero de gusano de Schwarzschild» producido por un agujero negro de Schwarzschild se considera infranqueable.
- El agujero de gusano supuestamente formado por un agujero negro de Reissner-Nordstrøm o Kerr-Newman, resultaría franqueable pero en una sola dirección, pudiendo contener un «agujero de gusano de Schwarzschild».
- El agujero de gusano de Lorentz posee masa negativa y se hipotetiza como franqueable en ambas direcciones (pasado/futuro).
Agujeros de gusano de Schwarzschild[editar]

Diagrama de un agujero de gusano de Schwarzschild.
Los agujeros de gusano de Lorentz, conocidos como agujeros de gusano de Schwarzschild, o puentes de Einstein-Rosen, son nexos que unen áreas de espacio que puede ser modeladas como soluciones de vacío en las ecuaciones de campo de Einstein, por unión de un modelo de un agujero negro y un modelo de un agujero blanco. Esta solución fue hallada por Albert Einstein y su compañero Nathan Rosen, que publicó primero el resultado en 1935. Sin embargo, en 1962, John A. Wheeler y Robert W. Fuller publicaron un artículo demostrando que este tipo de agujero de gusano es inestable, y se desintegraría instantáneamente tan pronto como se formase.
Antes de que los problemas de estabilidad de los agujeros de gusano de Schwarzschild se hiciesen evidentes, se propuso que los quásares podían ser agujeros blancos, formando así las zonas terminales de los agujeros de gusano de este tipo, sin embargo investigaciones más recientes descartan a los quásares como equiparables a los agujeros blancos.
Mientras los agujeros de gusano de Schwarzschild no sean atravesados, su existencia inspiró a Kip Thorne a imaginar agujeros de gusano atravesados creados por la sujeción de la «garganta» de un agujero de gusano de Schwarzschild abierto con materia exótica (materia que tiene masa/energía negativa).
Agujeros de gusano practicables[editar]

Imagen de un agujero de gusano practicable (que se puede atravesar) que conectaría el área frente al instituto de física de la Universidad de Tubinga con las dunas cerca de Boulogne sur Mer en el norte de Francia. La imagen ha sido recreada mediante un software de trazado de rayos en 4D en una métrica de Morris-Thorne, aunque los efectos gravitatorios sobre la longitud de onda no se han simulado.[3]
Los agujeros de gusano atravesables de Lorentz permitirían viajar de una parte del Universo a otra de ese mismo Universo muy deprisa o permitirían el viaje de un Universo a otro. Los agujeros de gusano conectan dos puntos del espacio-tiempo, lo cual quiere decir que permitirían el viaje en el tiempo así como también en espacio. La posibilidad de agujeros de gusano atravesados en la relatividad general fue primero demostrada por Kip S. Thorne y su graduado Mike Morris en un artículo publicado en 1988. El tipo de agujero de gusano atravesado que ellos descubrieron, se mantenía abierto por una especie de concha esférica de materia exótica, denominado como agujero de gusano de Morris-Thorne. Posteriormente se han descubierto otros tipos de agujeros de gusano atravesados como posibles soluciones en la relatividad general, como un tipo de agujero que se mantiene abierto por cuerdas cósmicas, el cual ya fue predicho por Matt Visser en un artículo publicado en 1989.
Base teórica[editar]
La definición topológica de agujero de gusano no es intuitiva. Se dice que en una región compacta del espacio-tiempo existe un agujero de gusano cuando su conjunto frontera es topológicamente trivial pero cuyo interior no es simplemente conexo. Formalizar esta idea conduce a definiciones como la siguiente, tomada del Lorentzian Wormholes de Matt Visser:
Si un espacio-tiempo de Lorentz contiene una región compacta Ω y si la topología de Ω es de la forma Ω ~ R x Σ, donde Σ es una 3-variedad de topología no trivial, cuya frontera tiene topología de la forma dΣ ~ S², y si además las hipersuperficies Σ son de tipo espacial, entonces, la región Ω contiene un agujero de gusano intra-universal cuasipermanente.
Caracterizar agujeros de gusano del inter-universo es más difícil. Por ejemplo, podemos imaginar un universo «recién nacido» conectado a su «universo progenitor» por un «ombligo» estrecho. Cabría considerar el ombligo como la garganta de un agujero de gusano, por la cual el espacio-tiempo está conectado.
Plausibilidad[editar]
En marzo de 2005, Amos Ori visualizó un agujero de gusano que permitía viajar en el tiempo, sin precisar materia exótica y satisfaciendo todas las condiciones energéticas. La estabilidad de esta solución es incierta, por lo que sigue sin estar claro si se requeriría una precisión infinita para que se formase y permitiese el viaje en el tiempo, y también si los efectos cuánticos protegerían la secuencia cronológica del tiempo en este caso.
Métrica de los agujeros de gusano[editar]
Las teorías sobre la métrica de los agujeros de gusano describen la geometría del espacio-tiempo de un agujero de gusano y sirven de modelos teóricos para el viaje en el tiempo. Un ejemplo simple de la métrica de un agujero de gusano atravesado podría ser el siguiente:
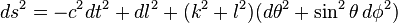
Un tipo de métrica de agujero de gusano no atravesado es la solución de Schwarzschild:

Agujeros de gusano y viajes en el tiempo[editar]

Interpretación artística de un agujero de gusano como debiera ser visto por un observador que estuviera atravesando el horizonte de sucesos de un agujero de gusano de Shwarzschild, el cual es similar a un agujero negro de Schwarzschild pero con la característica de poseer en substitución de la región en que se debiera encontrar la singularidad gravitacional (en el caso del agujero negro) un camino inestable hacia un agujero blanco que existiría en otro universo (véase multiverso). Esta región es inaccesible en el caso de un agujero de gusano de Schwarzschild, en cuanto el puente entre el agujero negro y el agujero blanco colapsaría siempre antes de que el observador tenga tiempo de atravesarlo. Véase White Holes and Wormholes para una discusión más técnica y una animación que representa lo que un observador podría ver cayendo en un agujero de gusano de tipo Schwarzschild.
Un agujero de gusano podría permitir en teoría el viaje en el tiempo. Esto podría llevarse a cabo acelerando el extremo final de un agujero de gusano a una velocidad relativamente alta respecto de su otro extremo. La dilatación de tiempo relativista resultaría en una boca del agujero de gusano acelerada envejeciendo más lentamente que la boca estacionaria, visto por un observador externo, de forma parecida a lo que se observa en la paradoja de los gemelos. Sin embargo, el tiempo pasa diferente a través del agujero de gusano respecto del exterior, por lo que, los relojes sincronizados en cada boca permanecerán sincronizados para alguien viajando a través del agujero de gusano, sin importar cuanto se muevan las bocas. Esto quiere decir que cualquier cosa que entre por la boca acelerada del agujero de gusano podría salir por la boca estacionaria en un punto temporal anterior al de su entrada si la dilatación de tiempo ha sido suficiente.
Por ejemplo, supongamos que dos relojes en ambas bocas muestran el año 2000 antes de acelerar una de las bocas y, tras acelerar una de las bocas hasta velocidades cercanas a la de la luz, juntamos ambas bocas cuando en la boca acelerada el reloj marca el año 2010 y en la boca estacionaria marca el año 2005. De esta forma, un viajero que entrara por la boca acelerada en este momento saldría por la boca estacionaria cuando su reloj también marcara el año 2005, en la misma región del espacio pero cinco años en el pasado. Tal configuración de agujeros de gusano permitiría a una partícula de la Línea de universo del espacio-tiempo formar un circuito espacio-temporal cerrado, conocido como curva cerrada de tipo tiempo. El curso a través de un agujero de gusano a través de una curva cerrada de tipo tiempo hace que un agujero de gusano tenga características de hueco temporal.
Se considera que es prácticamente imposible convertir a un agujero de gusano en una «máquina del tiempo» de este modo. Algunos análisis usando aproximaciones semiclásicas que incorporan efectos cuánticos en la relatividad general señalan que una retroalimentación de partículas virtuales circularían a través del agujero de gusano con una intensidad en continuo aumento, destruyéndolo antes de que cualquier información pudiera atravesarlo, de acuerdo con lo que postula la conjetura de protección cronológica. Esto ha sido puesto en duda, sugiriendo que la radiación se dispersaría después de viajar a través del agujero de gusano, impidiendo así su acumulación infinita. Kip S. Thorne mantiene un debate al respecto en su libro Agujeros negros y tiempo curvo (Black Holes and Time Warps).[4] También se ha descrito el denominado Anillo Romano, una configuración formada por más de un agujero de gusano. Este anillo parece permitir una línea de tiempo cerrado con agujeros de gusano estables cuando es analizado bajo el prisma de la gravedad semiclásica, pero sin una teoría completa de la gravedad cuántica aún no se puede saber si dicha aproximación semiclásica es aplicable en este caso.
|
|
|
|
Reply |
Message 5 of 6 on the subject |
|

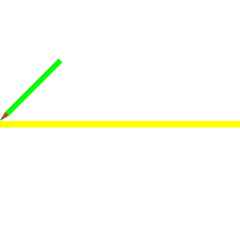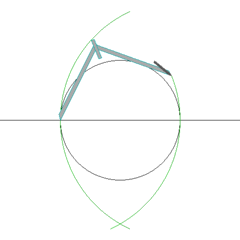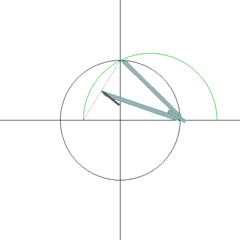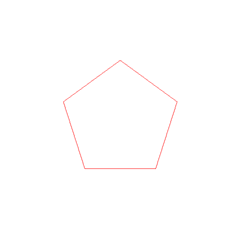
Sabemos que Vesica Piscis esta en funcion al a los 153 peces de Juan 21:11.
 Aqui tenemos a Pi - la circunferencia del toro y la vesica piscis 256/153 equivalente a la raiz cuadrada de 3 En el hipercubo las coordinadas binarias de Piscis son decimal 3 y binario 11 153 los pescados de Jesus en la biblia  
I have a lot to say about pythagorean triangles in my videos. In particular I have found many references to 5:12:13 triangles and 5:12 rectangles (that’s 2 of the triangles put together) in Stonehenge and the whole region surrounding it, in Washington DC, Paris, and Jerusalem. Someone who listened to my first Red Ice interview contacted me with a major discovery he made in regards to the 5:12 proportion. Brace yourself…

A rectangle measuring 5 feet by 12 feet has an area of 8640 square inches. This is something I can work with. I’m never going to be able to build an 864 foot solar Osiris talisman on a geodetic hot spot, but I think I can manage making a few raised garden beds measuring exactly 5 by 12 feet. And where I live in Canada (above 50 degrees North) can really use more resonance with the Sun.
If you saw SIPS Volume 1, you might recall that Stonehenge has its station stones which describe a 5×12 rectangle.

from SIPS Volume 1
Stonehenge is also 33.33° from Solomon’s Temple.

Sapientia Aedificavit Sibi Domum. Es decir, "la sabiduría ha edificado aquí su casa". Resulta curioso que la misma frase aparece en el Evangelio de María Magdalena, un texto apócrifo. Se dice que en el interior de esta iglesia y de otras muchas de Venecia está escondido el tesoro de los templarios. Pero no hay ninguna prueba de ello. Para terminar ya con esta entrada me gustaría que nos acercásemos un momento a uno de los edificios más emblemáticos de Venecia: el Palacio Ducal.
|
|
|
|
Reply |
Message 6 of 6 on the subject |
|
|
|
 First
First
 Previous
2 a 6 de 6
Next
Previous
2 a 6 de 6
Next
 Last
Last

|
|
| |
|
|
©2025 - Gabitos - All rights reserved | |
|
|

