|
|
General: LUGAR SANTISIMO (CUBO/HEXAGONO-ESPACIO/TIEMPO)=OCTAHEDRO (CLAVE JUBILEO)
Elegir otro panel de mensajes |
|
|
HEXAGONO=OCTAHEDRO =ESTRELLA DE 6 PUNTAS= SATURNO =CUBO/HEXAGONO= ESPACIO/TIEMPO =1 DE REYES 6:20 Y APOCALIPSIS 21:16
EL SEXTO DIA ES EL VIERNES Y EL OCTAVO EL DOMINGO. INCREIBLE
|
|
|
|
|
|
|
|
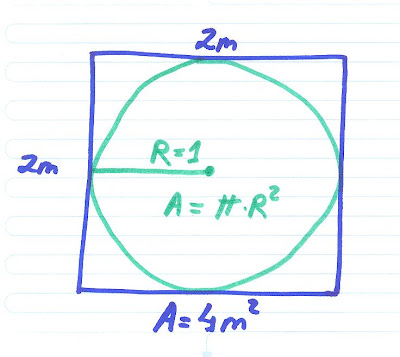
CUADRADO INSCRITO
LADO CUADRADO=2
SUPERFICIE CUADRADO=4
SUPERFICIE CIRCULO=6.28
CUADRADO CIRCUNSCRITO
LADO CUADRADO=2
SUPERFICIE CUADRADO=4
SUPERFICIE CIRCULO=3.14
|
|
|
|
|
|
|
|
Pi: la matemática no es democrática
3 de Diciembre de 2014 Publicado por Esteban Galisteo Gámez
La historia de la ciencia está llena de capítulos y anécdotas en ricas en términos de enseñanzas filosóficas. Algunas de tales historias son bastante divertidas, como la que vamos a narrar aquí sobre el número π, Pi. Más que un capítulo de la historia de la ciencia, se trata de una anécdota política relacionada con la ciencia, concretamente con el valor de Pi. Se trata de la historia de cómo el estado de Indiana (Estados Unidos) intentó promulgar una ley en virtud de la cual el valor de Pi sería 3.2, en lugar de 3.1415926…
La ley sobre el valor de π
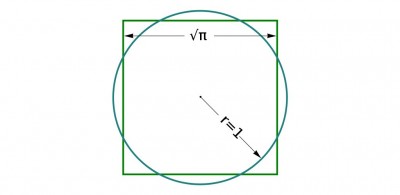
La cuadratura del círculo es un viejo problema
Todo comienza a partir de las excentricidades de un médico aficionado a las matemáticas, Edwin J. Goodwin, quien en 1897, convencido de haber descubierto un método para llevar a cabo la cuadratura del círculo, le propuso a Tylor I. Record, representante de Indiana en la Asamblea legislativa, un proyecto de ley. La idea era que en dicho proyecto se presentaba una “nueva verdad matemática”, que suponía una contribución a la educación y se permitía el uso exclusivo de forma gratuita de dicha verdad matemática al Estado de Indiana.
Parece una broma, pero es cierto. El proyecto de ley fue algo que no tenía precedentes y que nadie sabía muy bien qué hacer con él. En primer lugar, fue enviado al Comité de Tierras Pantanosas y estos consideraron que no era de su competencia, así que fue transferido al Comité de Educación, el cual lo aprobó.
El debate acerca del proyecto no se había terminado todavía, cuando, el profesor C. A. Waldo se trasladó a la ciudad de Indianápolis. Era profesor de matemáticas en la Universidad de Purdue y su misión en esta ciudad era realizar algunas gestiones presupuestarias para la Academia de Ciencias de Indiana. El profesor Waldo no sospechaba que en el Estado Indiana, en el que ejercía la profesión de matemático, iban a cambiar el valor del número π porque un matemático había “descubierto” la cuadratura del círculo.
El caso es que uno de los miembros de la asamblea le proporcionó a Waldo una copia del proyecto de ley. Además, le propuso presentarle al genio matemático detrás del método para cuadrar el círculo, que requería que el valor de π fuera 3,2. El profesor no quiso conocer a tal “genio”, pues, según alegó, “ya conocía a tantos locos como estaba dispuesto a soportar”.
El profesor Waldo no podía dejar que tal proyecto fuera aprobado, así que logró convencer a varios senadores, los suficientes para que el proyecto fuera postergado indefinidamente.
¿Qué problema hay en este proyecto de ley?
Aunque fue conocido como “el proyecto de ley de pi”, lo cierto es que tal número no aparece escrito en ninguna parte en el texto, si bien muchas de las afirmaciones realizadas en el mismo son equivalentes a proclamar que el valor de pi es 3.2 y no 3.14159…
Ahora bien, como se ha dicho, el proyecto trataba sobre la cuadratura del círculo y esto Goodwin lo había comprendido de forma literal: pensaba que debía encontrar un cuadrado tal que su área fuera idéntica a la de un círculo dado, utilizando únicamente regla y compás. Sin embargo, resulta que Goodwin desconocía el requisito de que únicamente había que utilizar regla y compás.
Goodwin, al ignorar esto, pensó que la fórmula de Arquímedes para calcular el área de un círculo no suponía una solución al problema de la cuadratura del círculo, por ello pensó que su fórmula era errónea. Sin embargo, resulta que Arquímedes no pretendía resolver el problema de la cuadratura del círculo. Goodwin lo había pensado así porque desconocía el requisito mencionado.
Es más, cinco años antes del fenomenal descubrimiento de Goodwin, en 1882, el matemático Ferdinand Lindemann demostró que π era un número trascendente, esto es, un tipo de número irracional que no es raíz de ninguna ecuación algebraica y ello implicaba que era imposible la cuadratura del círculo con regla y compás.
|
|
|
|
|
Decoding the Pyramids of Giza – Part 1
Copyright 2012 by World-Mysteries.com
Please quote with appropriate credit and copyright information
Introduction
Our ancestors, however long ago they may have lived and whatever part of the globe they may have occupied, were no idiots. Sad to say, over the last thirty years there have been many books on ancient technology that are not only ill researched but that also have an “ax to grind”. Most commonly this has been a desire to attribute the wonders of the ancient world to the efforts of “ancient astronauts.”
While we should not dismiss the possibility of past extraterrestrial contact out of hand, we should firmly reject the assumption that the technological advances of the ancient world were only achieved because of some kind of “outside help.” To us this seems like a kind of racism, in which our ancestors are looked down on simply because they lived in the past. The ancient-astronaut theories are only plausible if we denigrate the intelligence and abilities of ancient civilizations.
A popular misconception exists that the builders of the pyramids or the cave painters of prehistory were somehow less intelligent than we are. This simply isn’t true – there is no evidence that the human brain has evolved at all in the last fifty thousand years at least. Modern people are merely benefiting from thousands of years of accumulated knowledge and experimentation, not from increased intellect.
The relationship between number, proportion, astronomy and music must have been well known to the ancient people well before Greeks and Romans. Plato himself attested to the longevity of the Egyptian harmonic canon of proportion (sacred geometry), when he stated:
That the pictures and statues made ten thousand years ago, are in no one particular better or worse than what they now make.
The Ancient Egyptian works, large or small, are admired by all, because they are proportionally harmonious. This harmonic design concept is popularly known as “sacred geometry” and used in the design of sacred architecture and sacred art.
Proportions of any object are always independent of the units of length (meters, feet, cubits etc) we use to measure the object.
Once specific unit of measuring length is introduced, dimensions of an object can be expressed by different numbers, however its proportions will remain the same.
Although objects with identical proportions can be built to different scale, the “base to height” ratio will stay the same.
For example:
- for any circle, the circumference divided by its diameter is always equal “pi” (3.14159…)
- for any square, the perimeter divided by the diagonal is always 2 x sqrt(2) = 2.8284….
- for any equilateral triangle, the perimeter divided by the height is always 2 x sqrt(3) = 3.4641…
and the ratio height to base is (1/2)x sqrt(3) =0.866…
If we consider proportions of a pyramid expressed by the height divided by the base, values of the “base to height ratio” will be independent of units of measure we use! (see example of the GP below)
Proportions of the Giza Pyramids
Here are official dimensions of 3 pyramids at Giza:
- The Great Pyramid: Base =440 Royal Egyptian Cubits,
Height = 280 Royal Egyptian Cubits,
Base to Height ratio = 11/7 (440/280 = 11/7 exactly)
- The Second Pyramid:
Base =411 Royal Egyptian Cubits,
Height = 274 Royal Egyptian Cubits,
Base to Height ratio = 3/2 (411/274 = 3/2 exactly)
- The Third Pyramid:
Base =200 Royal Egyptian Cubits,
Height = 125 Royal Egyptian Cubits,
Base to Height ratio = 8/5 (200/125 = 8/5 exactly)
We can notice the following numerological relationships between 3 pyramids:
11 / 7 = (3 + 8) / (2 + 5)
( we are adding to top value of 2nd and 3rd pyramid ratio to the bottom value of each ratio)
If we add this way all 3 ratios we will get:
(11 + 8 + 3) / (7 + 5 +2) = 22/14 = 11/7
(the ratio of the Great Pyramid and the approximation of “pi” ).
So ratios of all 3 pyramids added this way are equal the ratio of the 1st pyramid.
Sir Petrie has noticed that the relation between the height and the base (ratio 3/2 = 6/4) conceal the Pythagorean Triangle (the first “Pythagorean Triplet”):
32 + 42 = 52
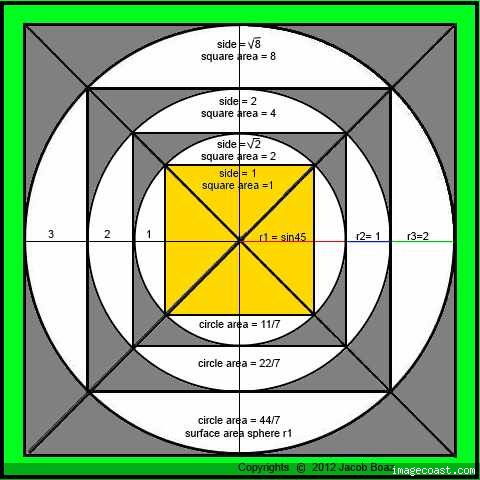
- The 3rd Pyramid with its base = 200 has diagonal = 282.84 = 100*2*sqrt(2).
- Radius of a circle circumscribed on 200*200 square is 141.4215 = 100* sqrt(2) and the circle’s circumference = 888.
- For this pyramid: base * height = 200 * 125 = 1000 * 25 (1000 is the scale of the Giza pyramids layout and 25 is the scale of the 3rd pyramid).
- Circle with radius=250 is very special since its circumference = 1570.8 = 1000* (1/2) * Pi
Base1+Base2+Base3+Height1+Height2+Height3=
440+411+200+280+274+125 = 1051 + 679 = 1730
Interesting “numerological” connections:
- Proportions connection (purely “numerological”):
Design proportions for the 1st Pyramid 7:11;
7=5+2 and 11= 8+3; 7/11 = (5+2) / (8+3) from this proportion we generate these ratios: for the 2nd pyramid 5/8 and for the 3rd pyramid 2/3
Also 100x 11/7 = 157.1 which is scale factor for the layout ( 11/9 ) of 3 pyramids.
8 and 5 give scale factor for the 1st Pyramid (5×8=40=5×23=40)
2, 3, 5, 7, 8, 11 give scale factor for the 2nd Pyramid:
11×8+7x(5+2)=137 or 11×7+7×5+5×5= 137
- For the Fist Pyramid the scale factor is 40 and the ratio is 11:7
11 x 22 – 22 = 40
Connection with the Second Pyarmid:
(11+7) x 32 - 52 = 137
7x 42 + 52 =137 and 11 x 23 + 72 = 137 and 11.72 is approximately 137 (scale for the Second Pyramid), also 25 component is the same as the scale factor for the Third Pyramid
- For the Second Pyramid the scale factor is 137 and the ratio is 3:2 (9:6 or 6:4)
(3+2)x 33 +2 = 137 also (9+6)x 32 +2 = 137 and (6+4)x7x2 – 3 = 137, Interestingly, (3+2)x 23 = 40 (scale factor for the First Pyramid)
also, square Root of 137 is approximately 11.7 (11 and 7 are ratio numbers describing the First pyramid)
The Third Pyramid’s scale factor is 25 and the ratio is 8:5 (same as 40:25) 52=25,
The Pyramids of Giza Layout
Another interesting relationship is uncovered when we investigate the layout of the Giza pyramids.
Measured dimensions of the layout rectangle are 1732 Royal Egyptian Cubits by 1414 Royal Egyptian Cubits.
This dimensions are equivalent of sqrt(3) x 1,000 by sqrt(2) x 1,000.
We can say that 3 pyramids are inside the rectangle with proportions (side to side ratio) equal: sqrt(3) / sqrt(2) = sqrt(3/2) = 1.224745…
In other words, the sqrt of the ratio describing the 2nd pyramid (3/2) generates proportions of the Giza pyramids layout rectangle.
Note: The area of the rectangle is sqrt(3) x sqrt(2) = sqrt(6) = 2.4495
Perimeter of the Giza layout = 6,292 (RC) [= 2* 1000* sqrt(2) + 2*1000*sqrt(3)]
Circle with the same perimeter would have Radius = 1,001 RC [ 6292 = 2*pi*R so R=1,001 ]
Another amazing design feature:
- Scale of the Giza layout: 1,000
- Scale of the 1st pyramid: 40
(btw, it generates base to height ratio 8/5 for the 3rd pyramid: 8×5 = 40)
- Scale of the 3rd pyramid: 25
- the scales of the 1st and the 3rd pyramid generate also the ratio for the 3rd pyramid: 40/25 = 8/5
- 25 = 1000/40 (this number is generated by the scale of the layout/scale of the Great Pyramid)
- Scale of the 2nd pyramid is 137 (see the paragraph below about 137)
It generates 11, the key number for the 1st pyramid (1+3+7 = 11).
Ratio 3/2 of the 2nd pyramid describes triangle [31/2 ]2+ [21/2 ]2= [51/2]2
which generates sides of the pyramids layout and its diagonal 51/2 in scale 1:1000
|
|
|
|
|
Nos empeñamos en resolver ese problema irresoluble que los matemáticos desde la antiguedad habian querido resolver que no era otro que cuadrar un círculo con escuadra y compás. Utilizando un simil aplicadolo al sector de las agencias de viajes en cuanto al desarrollo de las aplicaciones móviles la cuadratura consiste en conseguir generar apps comerciales para agencias de viajes con los requerimientos de ser nativas, personalizadas, a bajo coste y completamente automatizadas en la alimentación de contenidos, eso del bueno, bonito y barato de toda la vida pero elevado a la enésima potencia.
 Es por todos conocidos el coste prohibitivo del desarrollo de apps nativas y el listón es alto por tanto para conseguir un beneficio real y un ROI que mejore los resultados de la empresa gracias a la tecnología móvil, pero asumir inversiones elevadas para puntos de venta con un alcance comercial limitado, convierte la tan ansiada rentabilidad en todo un imposible para casi cualquier pyme tradicional de intermediación turística.
La revolución móvil es una realidad absoluta y todos los sectores económicos necesitan buscar su propio acomodo en el uso de las tecnologías móviles. En especial el sector del viaje y toda su cadena de valor necesitan llegar al cliente final con propuestas ofertadas a través de todos los canales posibles y el mobilees el que mayor potencial de desarrollo tiene en estos momentos pero huérfano de soluciones para el sector que nos atañe.
|
|
|
|
|
|
|
|
|
The man in the middle, whether it be Jupiter, Zeus, or Jesus is always depicted using the same fundamental concepts.
Jesus must come to terms with his inner and outer forces.
What if the yin and yang are the two thieves flanking Christ, the positive and the negative, the light (venus/sun) and the darkness (neptune/pluto)?
~end of UPDATE~
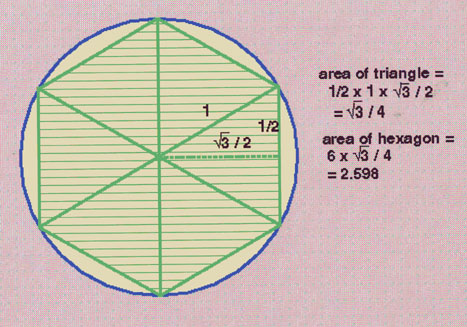
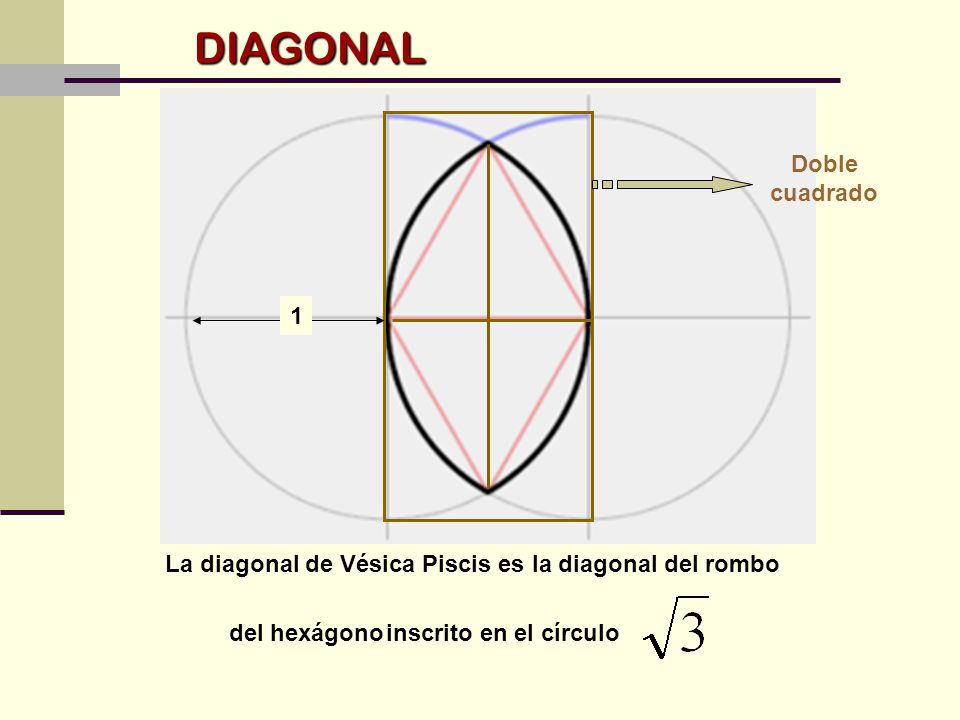
The mathematical ratio of the height of the vesica piscis to the width across its center is the square root of 3, or 1.7320508… (since if straight lines are drawn connecting the centers of the two circles with each other and with the two points where the circles intersect, two equilateral triangles join along an edge). The ratios 265:153 = 1.7320261… and 1351:780 = 1.7320513… are two of a series ofapproximations to this value, each with the property that no better approximation can be obtained with smaller whole numbers. Archimedes of Syracuse, in his On the Measurement of the Circle, uses these ratios as upper and lower bounds:
|
|
|
|
|
|
|
Also: “Harleston says of Teotihuacan’s builders: ‘When they draw a line, they’re telling you an area. When they draw an area, they’re telling you a volume. When they put volume, they’re telling you time.”
Geodesy and geodetic placement of “sacred sites” of ancient origins has long been affirmatively suspect – especially, the Great Pyramid of Giza. Geodesy involves a fundamental understanding of plane or solid geometry, astronomy relative to latitude and longitude with latitude of more recent vintage since ships-clock (cir. 1540) came into vogue. These geodetic or geometric relationships both on earth and in the heavens are a frequent haunt of pagans and occultists and of novel interest to science – though science with its unfortunate proliferation of skeptic is apt to go off into “metric tangents” and miss out on all the “fun!” “For quite some time researchers have been documenting the astronomical alignments of ancient archaeological and megalithic stone sites all over the world. But discovery of their geodesic alignment has been more recent. Geodesy refers to the theory and practice of surveying to determine the position of specific points on Earth’s surface. It is distinguished from plane surveying in that it deals with areas whose dimensions are so great that the curvature of the Earth must be taken into account. Geometric geodesy involves the creation of a mathematical model of Earth, while physical geodesy studies Earth’s gravity field. The discovery of the precise alignment of Mayan sites along the 90th parallel is significant because it demonstrates that the Maya were aware of Earth’s curvature and knew the advanced formulas used in geodesy.
Note: Carl Munck, archaeocryptographer, introduces an ancient Pyramid Matrix, in which ancient monuments – across the globe – encode their exact positions with respect to latitude and longitude. The science of decoding these monuments is called archaeocryptography. For latitude, ancient monuments were referenced to the same (modern) equator. For longitude, these monuments were referenced to a former Giza, Egypt Prime Meridian – discovered by Munck – that ran from pole to pole across the Great Pyramid.
|
|
|
|
|
Sólido de Kepler-Poinsot
Los sólidos de Kepler-Poinsot con sus símbolos de Schläfli.
Un sólido de Kepler (también llamado sólido de Kepler-Poinsot) es un poliedro regular no convexo, cuyas caras son todas polígonos regulares y que tiene en todos sus vértices el mismo número de caras concurrentes (compárese con los sólidos platónicos).
Existen sólo cuatro tipos, con las denominaciones siguientes:
Las caras están solo parcialmente en la superficie del sólido, y las partes expuestas están sólo conectadas en puntos (si están conectadas de algún modo). Si las partes se cuentan como caras separadas, el sólido deja de ser regular.
Características
Un sólido de Kepler cubre su esfera circunscrita más de una vez (con una esfera interior y otra exterior), con los centros de las caras como puntos direccionales en los sólidos que tienen caras en forma de pentagrama, mientras que en los otros son los vértices los que cumplen esa función. Por esta razón, no son necesariamente equivalentes topológicos de la esfera como lo son los sólidos platónicos, y en particular la característica de Euler V − E + F = 2 se verifica solamente para el Gran dodecaedro estrellado y para el Gran icosaedro.
Esto dependerá de cómo se observe el poliedro. Considérese, por ejemplo, el pequeño dodecaedro estrellado.1 Consiste en un dodecaedro con una pirámide pentagonal en cada una de sus 12 caras. En consecuencia, las 12 caras se extienden a pentagramas con el pentágono central dentro del sólido. La parte externa de cada cara consiste en cinco triángulos conectados por sólo cinco puntos. Si se cuentan separadamente, hay 60 caras (pero estas son triángulos isósceles que no son polígonos regulares, en cuyo caso seria un pentaquisdodecaedro). De modo similar, cada lado puede ser contado como tres, pero entonces los habrá de dos tipos. Igualmente, con los "cinco puntos" antes mencionados: en total habrá 20 puntos que pueden contarse como vértices, por lo que habrá un total de 32 vértices (otra vez, de dos tipos). Ahora la ecuación de Euler se verifica: 60 - 90 + 32 = 2.
Tipos
Hay cuatro sólidos de Kepler distintos:
Los dos primeros son estrellamientos, es decir, sus caras son convexas. Los otros dos tienen caras cóncavas, pero cada par de caras que se encuentra en un vértice de hecho lo hace en dos.
Historia
Mosaico del suelo en la basílica de San Marcos, a veces atribuido a Paolo Uccello.
La mayoría de los poliedros de Kepler-Poinsot, si no todos, eran ya conocidos de una forma u otra antes de Kepler. Un pequeño dodecaedro estrellado aparece en una tarsia de mármol (panel de incrustaciones) en el suelo de la basílica de San Marcos de Venecia, Italia. Data del siglo XV y, a veces se atribuye a Paolo Uccello. Wenzel Jamnitzer, en su obra Perspectiva corporum regularium (Perspectivas de los sólidos regulares), un libro de grabados en madera publicado en el siglo XVI, representa el gran dodecaedro y el gran dodecaedro estrellado.2 Se desprende de la disposición general del libro que consideraba solamente los cinco sólidos platónicos como regulares, y no comprendía la naturaleza periódica de sus grandes dodecaedros.
El pequeño y gran dodecaedro estrellado, a veces llamados poliedros de Kepler, fueron reconocidos por primera vez como regulares por Johannes Kepler en 1619, cuando notó que los dodecaedros estrellados (tanto el grande como el pequeño) se componían de dodecaedros "ocultos" (con caras pentagonales) que tienen caras compuestas de triángulos, tomando la apariencia de estrellas estilizadas. Los obtuvo por estelación del dodecaedro regular convexo, por primera vez, tratándolo como una superficie en lugar de un sólido. Se dio cuenta de que extendiendo los bordes o caras del dodecaedro convexo hasta que se encontrasen de nuevo, se podían obtener pentágonos estrellados. De esta manera construyó los dos dodecaedros estrellados, cada uno con la región convexa central de cada cara "oculta" en el interior, sólo con los brazos triangulares visibles. El paso final de Kepler fue reconocer que estos poliedros se ajustaban a la definición de regularidad, aunque fueran cóncavos en lugar de convexos, como sí lo eran los tradicionales sólidos platónicos.
En 1809, Louis Poinsot redescubrió las figuras de Kepler, mediante el ensamblaje de pentágonos estrellados alrededor de cada vértice. También montó polígonos convexos alrededor de los vértices de las estrellas para descubrir dos estrellas más regulares, el gran icosaedro y el gran dodecaedro. Por ello, algunos llaman a estos dos los poliedros de Poinsot. Poinsot no sabía si había descubierto todos los poliedros regulares estrellados.
Tres años más tarde, Augustin Cauchy demostró que la lista por estelación de los sólidos platónicos estaba completa, y casi medio siglo después, en 1858, Joseph Louis François Bertrandproporcionó una prueba más elegante por facetado de ellas.
Al año siguiente, Arthur Cayley dio a los poliedros de Kepler–Poinsot los nombres por los que generalmente conocidos hoy.
Unos cien años más tarde, John Conway desarrolló una terminología sistemática para las estelaciones hasta un máximo de cuatro dimensiones. Dentro de este esquema, sugirió nombres ligeramente modificados para dos de los poliedros regulares estrellados. Los nombres de Conway han sido considerados de utilidad, pero no han sido ampliamente adoptados.
| Nombre de Cayley |
pequeño dodecaedro estrellado |
gran dodecaedro |
gran dodecaedro estrellado |
gran icosaedro |
| Nombre de Conway |
dodecaedro estrellado |
gran dodecaedro (sin cambio) |
dodecaedro grande estrellado |
gran icosaedro (sin cambio) |
https://es.wikipedia.org/wiki/S%C3%B3lido_de_Kepler-Poinsot |
|
|
 First Previous 2 to 5 of 5 Next  Last |
|
|
Posted in Azulejos-Mosaicos, Italia, Templo with tags Poliedros on 7 junio 2012 by angelrequena
Hace tiempo hablamos del conocido pequeño dodecaedro estrellado del pavimento de la puerta de salida derecha del duomo de San Marcos. No es el único de la catedral veneciana: apenas visible para la visita ordinaria hay otro más pequeño, justo debajo del iconostasio en su centro, en lugar preferente y en línea con el altar.
Si se entra hacia la Pala de Oro puede verse una mancha central en la lejanía pero casi sin distinguirse. En mi última visita tuve la gran suerte de encontrar un ordenanza amable que encendía las luces a un grupo concertado que me permitió verlo y fotografiarlo. No desmerece de su hermano mayor, si cabe revela mayor virtuosismo y ostentación del dominio de la perspectiva matemática.
Hay cuatro sólidos regulares cóncavos, los dos de Poinsot y los dos de Kepler. Venecia nos ofrece los dos de Kepler en San Pantaleone y uno en San Marcos pero en dos lugares, uno alejado para despedirse del templo y otro en el lugar más destacado: la entrada central al recinto más sagrado.
El dodecaedro estrellado de la puerta (abajo) solo tiene una corona de taracea marmórea complementaria mientras que el del iconostasio (arriba) tiene tres.
3 Comments »
https://mateturismo.wordpress.com/tag/poliedros/page/7/
|
|
|
|
|
|
 Primer
Anterior
15 a 29 de 44
Siguiente
Último
|
|
| |
|
|
©2024 - Gabitos - Todos los derechos reservados | |
|
|
