|
|
General: APOCALIPSIS 21, JUAN MARCOS Y LOS "VIAJES EN EL TIEMPO"
Elegir otro panel de mensajes |
|
|
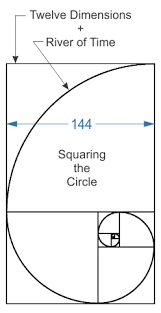
REPRODUCCION DE LOS CONEJOS EN FUNCION A LA SERIE DE FIBONACCI, INCLUSO DEL RELOJ Y DE LA MISMA SANTA CENA (MISMA MANZANA)
Apocalipsis 21
1. Vi un cielo nuevo y una tierra nueva; porque el primer cielo y la primera tierra pasaron, y el mar ya no existía más.
2. Y yo Juan vi la santa ciudad, la nueva Jerusalén, descender del cielo, de Dios, dispuesta como una esposa ataviada para su marido.
3. Y oí una gran voz del cielo que decía: He aquí el tabernáculo de Dios con los hombres, y él morará con ellos; y ellos serán su pueblo, y Dios mismo estará con ellos como su Dios.
4. Enjugará Dios toda lágrima de los ojos de ellos; y ya no habrá muerte, ni habrá más llanto, ni clamor, ni dolor; porque las primeras cosas pasaron.
5. Y el que estaba sentado en el trono dijo: He aquí, yo hago nuevas todas las cosas. Y me dijo: Escribe; porque estas palabras son fieles y verdaderas.
6. Y me dijo: Hecho está. Yo soy el Alfa y la Omega, el principio y el fin. Al que tuviere sed, yo le daré gratuitamente de la fuente del agua de la vida. (911 O SALMO 119)
7. El que venciere heredará todas las cosas, y yo seré su Dios, y él será mi hijo.
8. Pero los cobardes e incrédulos, los abominables y homicidas, los fornicarios y hechiceros, los idólatras y todos los mentirosos tendrán su parte en el lago que arde con fuego y azufre, que es la muerte segunda.
9. Vino entonces a mí uno de los siete ángeles que tenían las siete copas llenas de las siete plagas postreras, y habló conmigo, diciendo: Ven acá, yo te mostraré la desposada, la esposa del Cordero.
10. Y me llevó en el Espíritu a un monte grande y alto, y me mostró la gran ciudad santa de Jerusalén, que descendía del cielo, de Dios,
11. teniendo la gloria de Dios. Y su fulgor era semejante al de una piedra preciosísima, como piedra de jaspe, diáfana como el cristal.
12. Tenía un muro grande y alto con doce puertas; y en las puertas, doce ángeles, y nombres inscritos, que son los de las doce tribus de los hijos de Israel; (EL MISMO RELOJ, O SANTA CENA O LA MANZANA, LA TRASLACION EN EL TIEMPO)
13. al oriente tres puertas; al norte tres puertas; al sur tres puertas; al occidente tres puertas.
14. Y el muro de la ciudad tenía doce cimientos, y sobre ellos los doce nombres de los doce apóstoles del Cordero.
15. El que hablaba conmigo tenía una caña de medir, de oro, para medir la ciudad, sus puertas y su muro.
16. La ciudad se halla establecida en cuadro, y su longitud es igual a su anchura; y él midió la ciudad con la caña, doce mil estadios; la longitud, la altura y la anchura de ella son iguales. (CUBO=ESPACIO/TIEMPO)
HEXAGONO=OCTAHEDRO =ESTRELLA DE 6 PUNTAS= SATURNO =CUBO/HEXAGONO= ESPACIO/TIEMPO =1 DE REYES 6:20 Y APOCALIPSIS 21:16
EL SEXTO DIA ES EL VIERNES Y EL OCTAVO EL DOMINGO. INCREIBLE
17. Y midió su muro, ciento cuarenta y cuatro codos, de medida de hombre, la cual es de ángel. (EL NEXO DE LA MANZANA, EL PENTAGONO, LA NUEVA JERUSALEN, EL CASTILLO SAN ANGELO DEL VATICANO E INCLUSO EL MISMO PENTAGONO DE WASHINGTON D.C. ES OBVIO EL NEXO DEL RELOJ CON LA MANZANA)
18. El material de su muro era de jaspe; pero la ciudad era de oro puro, semejante al vidrio limpio;
19. y los cimientos del muro de la ciudad estaban adornados con toda piedra preciosa. El primer cimiento era jaspe; el segundo, zafiro; el tercero, ágata; el cuarto, esmeralda;
20. el quinto, ónice; el sexto, cornalina; el séptimo, crisólito; el octavo, berilo; el noveno, topacio; el décimo, crisopraso; el undécimo, jacinto; el duodécimo, amatista.
21. Las doce puertas eran doce perlas; cada una de las puertas era una perla. Y la calle de la ciudad era de oro puro, transparente como vidrio.
22. Y no vi en ella templo; porque el Señor Dios Todopoderoso es el templo de ella, y el Cordero.
23. La ciudad no tiene necesidad de sol ni de luna que brillen en ella; porque la gloria de Dios la ilumina, y el Cordero es su lumbrera. (PROVERBIOS 25:11, OSEA LA MISMA MANZANA, OSEA UNA REFERENCIA AL SOL/ORO/HOMBRE Y LUNA/PLATA/MUJER, OSEA EL MISMO SUEÑO DE JOSE DE GENESIS 37)
24. Y las naciones que hubieren sido salvas andarán a la luz de ella; y los reyes de la tierra traerán su gloria y honor a ella.
25. Sus puertas nunca serán cerradas de día, pues allí no habrá noche.
26. Y llevarán la gloria y la honra de las naciones a ella.
27. No entrará en ella ninguna cosa inmunda, o que hace abominación y mentira, sino solamente los que están inscritos en el libro de la vida del Cordero.
|
|
|
|
|
|
|
|
Multimagic cubes
 John-R. Hendricks (Regina, Saskatchewan, Canada, 1929 - Victoria, BC, Canada, 2007) John-R. Hendricks (Regina, Saskatchewan, Canada, 1929 - Victoria, BC, Canada, 2007)
Why limit oneself to 2 dimensions of multimagic squares? The Canadian John-R. Hendricks, the world's foremost expert on magic squares, created in June 2000 the first known bimagic cube. So, this bimagic cube is also the first known multimagic cube. His remarkable cube is 25th-order (=25x25x25 sized), and contains all the numbers from 1 to 15,625. The magic sum is 195,325, and the bimagic sum is 2,034,700,525. Holger Danielsson has created a PDF document (510Kb) giving details of this cube. See the biography of John R. Hendricks. See also another biography published in the Journal of Recreational Mathematics.
However, I have big doubts on the paternity of this cube. In his "The Magic Square Course", second edition 1992 (very limited distribution as was the first edition 1991, only few photocopied samples), John-R. Hendricks wrote page 411 :
"David M. Collison, in an unpublished paper, has constructed a bimagic cube of order 25 (....) but it takes too much space to show here."
Look at page 411. We may think from this text that John had actually received the cube. And exactly the same order 25, a very strange coincidence! David M. Collison (1937 - 1991), an Englishman, was living in Anaheim, California: often mentioned in "The Magic Square Course", he sent a lot of discoveries directly to John, and died one year before this second edition. When John published the cube in 2000, he strangely forgot to mention that David had previously constructed such a cube...
In 2003, new multimagic cubes were constructed, thus giving now the following list of the smallest known cubes, for each multimagic level:
(*) All the cubes were created in 2003 by Christian Boyer, except this bimagic cube of order 25 created in 2000 by John R. Hendricks or before 1991 by David M. Collison.
The bimagic cube of order 16 uses the numbers from 0 to 4095. The magic sum is 32,760, and the bimagic sum is 89,445,720. The 256 rows, 256 columns, 256 pillars and 4 triagonals (= the 4 main space diagonals) are bimagic. Since it is not necessary by the definition of a standard magic cube, the 96 diagonals of the various squares making up the bimagic cube are not bimagic. Therefore they are magic. Thanks to Harvey Heinz (Canada), Aale de Winkel (Netherlands) and Walter Trump (Germany) who verified the bimagic characteristics of the cube as soon as it was announced in January 2003.
The trimagic cube of order 64 uses the numbers from 0 to 262,143. The 4096 rows, 4096 columns, 4096 pillars and 4 triagonals are trimagic. The 384 diagonals are bimagic.
A trimagic cube of order 256 has also been created: it is "perfect", since all its diagonals are trimagic. This cube is a monster: it contains the numbers from 0 to 16,777,215, with for example the trimagic sum S3 = 302231418874861348454400. Thanks to Walter Trump (Germany) who verified the trimagic characteristics of these cubes as soon as they were announced in February 2003.
Eric Weisstein (USA) also checked this perfect trimagic cube of order 256 using Mathematica on Dec 6, 2003 and confirmed its properties. The check took 30 minutes on a 1GHz Macintosh G4.
Then tetramagic cubes even more monstrous have been created, checked by Renaud Lifchitz (France) and Yves Gallot (France). See some details about these two persons in the hypercubes page.
About the perfect tetramagic cube 8192, its 67,108,864 rows, 67,108,864 columns, 67,108,864 pillars, 4 triagonals, and 49,152 diagonals are tetramagic. Its magic sums are :
- S1 = 2251799813681152
- S2 = 825293359521335050119065600
- S3 = 340282366919700523424090353056775929856
- S4 = 149657767662003894090216275236580155584753888727040
In honour of the year 2003 when all of the above multimagic cubes were created, all these cubes start with the number "2003" in their first corner!
In the September 2003 issue of Pour La Science, the French edition of Scientific American, I published an article about the history of magic cubes and about the construction of multimagic cubes. It is stated for example that my perfect tetramagic cube of order 8,192 is:
- So big that, if you built it (imagine each cell as a small wooden die of 2cm x 2cm x 2cm where a number of 12 digits maximum is engraved), you may include within the cube... Notre-Dame de Paris!
- So big that, if you check 1,000 dice (= 1000 numbers) per second, you will need more than 17 years to check the whole cube.
- So big that, if you engrave on each die the name of each person currently living on the earth (instead of the number used), only 1% of the dice will be engraved! 99% of the dice will remain blank.
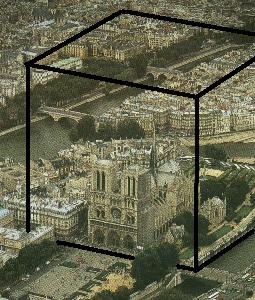
The perfect tetramagic cube of order 8,192 can easily include Notre-Dame de Paris!
|
I dedicate the tetramagic cubes to Gaston Tarry and André Viricel. Gaston Tarry, inventor of the term "tetramagic", is the first man to have constructed a trimagic square, in 1905. It was of order 128. He is also the first man to have proved the famous Euler conjecture of the 36 officers. And my old friend André Viricel is the man who has invented a powerful method to construct trimagic squares of order 32. All my multimagic constructions are based on the ideas of Gaston Tarry (later improved by General Cazalas) and André Viricel, ideas simply enhanced to work with higher order and higher dimensions, cubes and hypercubes. Christian Boyer
|
An anecdote found in the book Carrés Magiques au degré n, by Général Cazalas, 1934. Page 13, in the preface written by Auguste Aubry, we read that Gaston Tarry was preparing "a panmagic and trimagic cube that he had not the time to achieve" before he died in 1913. There is alas no trace of this work!
The Général Cazalas, although smart enough to construct his 64th-order trimagic square, later failed in his attempt to construct a bimagic cube. It is interesting to note that it was precisely focused, like John-R. Hendricks and David M. Collison, on the order 25. Cazalas wrote in 1934 in Sphinx (pages 168-169):
"... but the simplest bimagic cube is on the domain of the theory, because his order is too big: in a 25th-order cube, we even get only a very incomplete bimagic".
So, John-R. Hendricks / David M. Collison proved to be more cunning than Cazalas!
Zhong Ming's perfect bimagic cubes of orders 16 and 25
  Zhong Ming (on the right, with his son and his daughter in 2015) Zhong Ming (on the right, with his son and his daughter in 2015)
The above bimagic cubes of orders 16 and 25 are bimagic, but not perfect bimagic. My smallest perfect bimagic cube was big: of order 32, constructed in 2003.
In April 2015, Zhong Ming succeeded in constructing perfect bimagic cubes of orders 16 and 25; they are the new smallest known perfect bimagic cubes! Zhong Ming is a mathematics teacher, at Sichuan Dazhou Daxian, Pavilion Town Center School of China.
Return to the home page http://www.multimagie.com
http://www.multimagie.com/English/Cube.htm |
|
|
|
|
|
|
|
369
Last edited by science2art; 23-07-2012 at 01:21 PM.
|
|
|
|
|
PHI A NOTRE-DAME
A la catredal de Notre Dame hi observem més rectanlges auris: Creat per Mario Pastor  |
|
|
|
|
La proporción Áurea en la arquitectura
En el blog de Carpinterías para CTE queremos dar a conocer a arquitectos, ingenieros, constructores y gente afín a este mundo las virtudes del buen hacer. Para ello y en busca de la excelencia, queremos acercar al público el Código Técnico de la Edificación.
Presentamos Ferias, damos a conocer el PVC kömmerling, hablamos de los grandes maestros y damos consejos para mejorar profesionalmente.
Pero un buen arquitecto debe de estar entre dos mundos. Por un lado es un técnico, comprometido y entendido del buen hacer en su profesión. Del otro lado, es un artista, un humanista que debe dar soluciones siempre mejores y que sean capaces de cautivar el alma.
Hoy queremos centrarnos en esta nueva faceta que en cierta medida la burbuja inmobiliaria ha hecho que se le diera la espalda. Para ello no hay nada más apasionante que volver la vista atrás en busca del arte y de la magia que nos proporciona el Número Áureo. Un número que encontramos en la naturaleza, el espacio, las cosas cotidianas y por supuesto en el Arte y en la Arquitectura.
El numero Áureo, La Divina Proporción, Phi, Numero de Oro, existen innumerables nombres y escritos sobre este numero que se conoce desde la antigüedad. Según Euclides, uno de los primeros sabios en estudiarlo: ““Se dice que una línea recta está dividida entre el extremo y su proporcional cuando la línea entera es al segmento mayor como el mayor es al menor.” Aunque como hemos comentado, su aplicación es infinita, queremos centrarnos en ejemplos arquitectónicos que llevan el sello de este número fantástico.
Uno de los primeros ejemplos que encontramos son Las Pirámides de Egipto. El número áureo aparece hasta tres veces en las relaciones numéricas entre los distintos elementos de la pirámide.

Otro ejemplo de lo que es capaz de diseñar y construir el ser humano es El Partenón de Atenas. Rectángulos, diagonales, relaciones, hay muchas representaciones del número mágico en esta maravilla del mundo antiguo.

Obras mas recientes como la Catedral de Notre Damme en París consiguen su armonía utilizando el numero Phi.

También en París, la Torre Eiffel tiene proporciones Áureas en todo su desarrollo.

Le Corbusier no se limito a aplicar en sus proyectos este número. Quiso ir más allá y al estudiarlo profundamente desarrollo un nuevo sistema de medida más humano que todos conocemos como El Modulor.

Aunque podemos encontrarlo en muchos edificios y construcciones, también podemos verlo en muchas cosas que conocemos, sin importar la escala:
Una galaxia, la relación entre planetas, una caracola, un girasol, en La Gioconda o Mona Lisa, un iPod, un paquete de tabaco…
Lo que no hay duda es que guarda una relación intrínseca con lo que entendemos como belleza por lo que es esencial para cualquiera de las Bellas Artes que conocemos y la Arquitectura nunca puede ser una excepción.
http://www.ctearquitectura.es/actualidad/noticias/la-proporcion-aurea-en-la-arquitectura/ |
|
|
|
|
August 23, 2018/

The Golden Section (aka Golden Mean, and Golden Ratio) phys.org
We use math in architecture on a daily basis to solve problems. We use it to achieve both functional and aesthetic advantages. By applying math to our architectural designs through the use of the Golden Section and other mathematical principles, we can achieve harmony and balance. As you will see from some of the examples below, the application of mathematical principles can result in beautiful and long-lasting architecture which has passed the test of time.
Using Math in Architecture for Function and Form
We use math in architecture every day at our office. For example, we use math to calculate the area of a building site or office space. Math helps us to determine the volume of gravel or soil that is needed to fill a hole. We rely on math when designing safe building structures and bridges by calculating loads and spans. Math also helps us to determine the best material to use for a structure, such as wood, concrete, or steel.
“Without mathematics there is no art.” – Luca Pacioli, De divina proportione, 1509
Architects also use math when making aesthetic decisions. For instance, we use numbers to achieve attractive proportion and harmony. This may seem counter-intuitive, but architects routinely apply a combination of math, science, and art to create attractive and functional structures. One example of this is when we use math to achieve harmony and proportion by applying a well-known principle called the Golden Section
Math and Proportion – The Golden Section

Perfect proportions of the human body – The Vitruvian Man – by Leonardo da Vinci.
We tend to think of beauty as purely subjective, but that is not necessarily the case. There is a relationship between math and beauty. By applying math to our architectural designs through the use of the Golden Section and other mathematical principles, we can achieve harmony and balance.
The Golden Section is one example of a mathematical principle that is believed to result in pleasing proportions. It was mentioned in the works of the Greek mathematician Euclid, the father of geometry. Since the 4th century, artists and architects have applied the Golden Section to their work.
The Golden Section is a rectangular form that, when cut in half or doubled, results in the same proportion as the original form. The proportions are 1: the square root of 2 (1.414) It is one of many mathematical principles that architects use to bring beautiful proportion to their designs.
Examples of the Golden Section are found extensively in nature, including the human body. The influential author Vitruvius asserted that the best designs are based on the perfect proportions of the human body.
Over the years many well-known artists and architects, such as Leonardo da Vinci and Michelangelo, used the Golden Section to define the dimensions and proportions in their works. For example, you can see the Golden Section demonstrated in DaVinci’s painting Mona Lisa and his drawing Vitruvian Man.
Famous Buildings Influenced by Mathematical Principles
Here are some examples of famous buildings universally recognized for their beauty. We believe their architects used math and the principals of the Golden Section in their design:
Parthenon
The classical Doric columned Parthenon was built on the Acropolis between 447 and 432 BC. It was designed by the architects Iktinos and Kallikrates. The temple had two rooms to shelter a gold and ivory statue of the goddess Athena and her treasure. Visitors to the Parthenon viewed the statue and temple from the outside. The refined exterior is recognized for its proportional harmony which has influenced generations of designers. The pediment and frieze were decorated with sculpted scenes of Athena, the Gods, and heroes.

Parthenon Golden Section
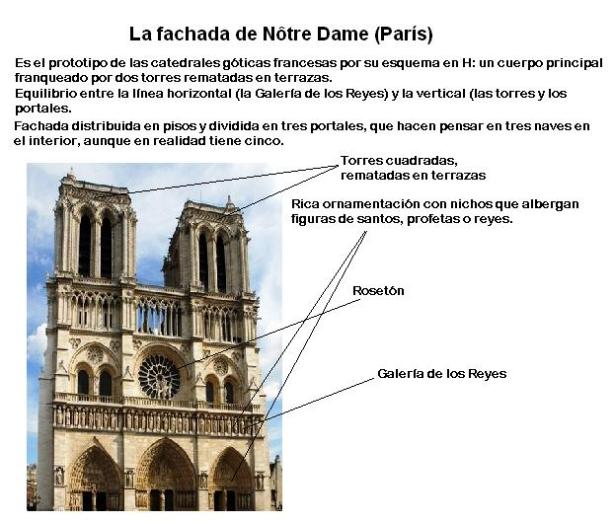
Notre Dame Cathedral in Paris
Built on the Ile de la Cite, Notre Dame was built on the site of two earlier churches. The foundation stone was laid by Pope Alexander III in 1163. The stone building demonstrates various styles of architecture, due to the fact that construction occurred for over 300 years. It is predominantly French Gothic, but also has elements of Renaissance and Naturalism. The cathedral interior is 427 feet x 157 feet in plan. The two Gothic towers on the west façade are 223 feet high. They were intended to be crowned by spires, but the spires were never built. The cathedral is especially loved for its three stained glass rose windows and daring flying buttresses. During the Revolution, the building was extensively damaged and was saved from demolition by the emperor Napoleon.

Notre Dame Cathedral in Paris
Taj Mahal
Built in Agra between 1631 and 1648, the Taj Mahal is a white marble mausoleum designed by Ustad-Ahmad Lahori. This jewel of Indian architecture was built by Emperor Shah Jahan in memory of his favorite wife. Additional buildings and elements were completed in 1653. The square tomb is raised and is dramatically located at the end of a formal garden. On the interior, the tomb chamber is octagonal and is surrounded by hallways and four corner rooms. Building materials are brick and lime veneered with marble and sandstone.

Taj Mahal designed by Ustad-Ahmad Lahori
As you can see from the above examples, the application of mathematical principles can result in some pretty amazing architecture. The architects’ work reflects eye-catching harmony and balance. Although these buildings are all quite old, their designs have pleasing proportions which have truly passed the test of time.
https://bleckarchitects.com/math-in-architecture/
|
|
|
|
|
|

LLAVE DE ORO Y DE PLATA AL IGUAL QUE LA MANZANA
Incendio Notre Dame: Última hora de la catedral de París (15 DE ABRIL)

 Incendio Notre Dame (París), en directo (Bertrand Guay / AFP)
PHI A NOTRE-DAME
A la catredal de Notre Dame hi observem més rectanlges auris: Creat per Mario Pastor 
The DaVinci Code, Notre Dame Cathedral from DaVinci Code
original movie prop

        

August 23, 2018/

The Golden Section (aka Golden Mean, and Golden Ratio) phys.org
We use math in architecture on a daily basis to solve problems. We use it to achieve both functional and aesthetic advantages. By applying math to our architectural designs through the use of the Golden Section and other mathematical principles, we can achieve harmony and balance. As you will see from some of the examples below, the application of mathematical principles can result in beautiful and long-lasting architecture which has passed the test of time.
Using Math in Architecture for Function and Form
We use math in architecture every day at our office. For example, we use math to calculate the area of a building site or office space. Math helps us to determine the volume of gravel or soil that is needed to fill a hole. We rely on math when designing safe building structures and bridges by calculating loads and spans. Math also helps us to determine the best material to use for a structure, such as wood, concrete, or steel.
“Without mathematics there is no art.” – Luca Pacioli, De divina proportione, 1509
Architects also use math when making aesthetic decisions. For instance, we use numbers to achieve attractive proportion and harmony. This may seem counter-intuitive, but architects routinely apply a combination of math, science, and art to create attractive and functional structures. One example of this is when we use math to achieve harmony and proportion by applying a well-known principle called the Golden Section
Math and Proportion – The Golden Section

Perfect proportions of the human body – The Vitruvian Man – by Leonardo da Vinci.
We tend to think of beauty as purely subjective, but that is not necessarily the case. There is a relationship between math and beauty. By applying math to our architectural designs through the use of the Golden Section and other mathematical principles, we can achieve harmony and balance.
The Golden Section is one example of a mathematical principle that is believed to result in pleasing proportions. It was mentioned in the works of the Greek mathematician Euclid, the father of geometry. Since the 4th century, artists and architects have applied the Golden Section to their work.
The Golden Section is a rectangular form that, when cut in half or doubled, results in the same proportion as the original form. The proportions are 1: the square root of 2 (1.414) It is one of many mathematical principles that architects use to bring beautiful proportion to their designs.
Examples of the Golden Section are found extensively in nature, including the human body. The influential author Vitruvius asserted that the best designs are based on the perfect proportions of the human body.
Over the years many well-known artists and architects, such as Leonardo da Vinci and Michelangelo, used the Golden Section to define the dimensions and proportions in their works. For example, you can see the Golden Section demonstrated in DaVinci’s painting Mona Lisa and his drawing Vitruvian Man.
Famous Buildings Influenced by Mathematical Principles
Here are some examples of famous buildings universally recognized for their beauty. We believe their architects used math and the principals of the Golden Section in their design:
Parthenon
The classical Doric columned Parthenon was built on the Acropolis between 447 and 432 BC. It was designed by the architects Iktinos and Kallikrates. The temple had two rooms to shelter a gold and ivory statue of the goddess Athena and her treasure. Visitors to the Parthenon viewed the statue and temple from the outside. The refined exterior is recognized for its proportional harmony which has influenced generations of designers. The pediment and frieze were decorated with sculpted scenes of Athena, the Gods, and heroes.

Parthenon Golden Section
Notre Dame Cathedral in Paris
Built on the Ile de la Cite, Notre Dame was built on the site of two earlier churches. The foundation stone was laid by Pope Alexander III in 1163. The stone building demonstrates various styles of architecture, due to the fact that construction occurred for over 300 years. It is predominantly French Gothic, but also has elements of Renaissance and Naturalism. The cathedral interior is 427 feet x 157 feet in plan. The two Gothic towers on the west façade are 223 feet high. They were intended to be crowned by spires, but the spires were never built. The cathedral is especially loved for its three stained glass rose windows and daring flying buttresses. During the Revolution, the building was extensively damaged and was saved from demolition by the emperor Napoleon.

Notre Dame Cathedral in Paris
Taj Mahal
Built in Agra between 1631 and 1648, the Taj Mahal is a white marble mausoleum designed by Ustad-Ahmad Lahori. This jewel of Indian architecture was built by Emperor Shah Jahan in memory of his favorite wife. Additional buildings and elements were completed in 1653. The square tomb is raised and is dramatically located at the end of a formal garden. On the interior, the tomb chamber is octagonal and is surrounded by hallways and four corner rooms. Building materials are brick and lime veneered with marble and sandstone.

Taj Mahal designed by Ustad-Ahmad Lahori
As you can see from the above examples, the application of mathematical principles can result in some pretty amazing architecture. The architects’ work reflects eye-catching harmony and balance. Although these buildings are all quite old, their designs have pleasing proportions which have truly passed the test of time.
https://bleckarchitects.com/math-in-architecture/
|
|
|
|
|
|
|




|

LLAVE DE ORO Y DE PLATA AL IGUAL QUE LA MANZANA
Incendio Notre Dame: Última hora de la catedral de París (15 DE ABRIL)

 Incendio Notre Dame (París), en directo (Bertrand Guay / AFP)
PHI A NOTRE-DAME
A la catredal de Notre Dame hi observem més rectanlges auris: Creat per Mario Pastor 
The DaVinci Code, Notre Dame Cathedral from DaVinci Code
original movie prop
 
        

August 23, 2018/

The Golden Section (aka Golden Mean, and Golden Ratio) phys.org
We use math in architecture on a daily basis to solve problems. We use it to achieve both functional and aesthetic advantages. By applying math to our architectural designs through the use of the Golden Section and other mathematical principles, we can achieve harmony and balance. As you will see from some of the examples below, the application of mathematical principles can result in beautiful and long-lasting architecture which has passed the test of time.
Using Math in Architecture for Function and Form
We use math in architecture every day at our office. For example, we use math to calculate the area of a building site or office space. Math helps us to determine the volume of gravel or soil that is needed to fill a hole. We rely on math when designing safe building structures and bridges by calculating loads and spans. Math also helps us to determine the best material to use for a structure, such as wood, concrete, or steel.
“Without mathematics there is no art.” – Luca Pacioli, De divina proportione, 1509
Architects also use math when making aesthetic decisions. For instance, we use numbers to achieve attractive proportion and harmony. This may seem counter-intuitive, but architects routinely apply a combination of math, science, and art to create attractive and functional structures. One example of this is when we use math to achieve harmony and proportion by applying a well-known principle called the Golden Section
Math and Proportion – The Golden Section

Perfect proportions of the human body – The Vitruvian Man – by Leonardo da Vinci.
We tend to think of beauty as purely subjective, but that is not necessarily the case. There is a relationship between math and beauty. By applying math to our architectural designs through the use of the Golden Section and other mathematical principles, we can achieve harmony and balance.
The Golden Section is one example of a mathematical principle that is believed to result in pleasing proportions. It was mentioned in the works of the Greek mathematician Euclid, the father of geometry. Since the 4th century, artists and architects have applied the Golden Section to their work.
The Golden Section is a rectangular form that, when cut in half or doubled, results in the same proportion as the original form. The proportions are 1: the square root of 2 (1.414) It is one of many mathematical principles that architects use to bring beautiful proportion to their designs.
Examples of the Golden Section are found extensively in nature, including the human body. The influential author Vitruvius asserted that the best designs are based on the perfect proportions of the human body.
Over the years many well-known artists and architects, such as Leonardo da Vinci and Michelangelo, used the Golden Section to define the dimensions and proportions in their works. For example, you can see the Golden Section demonstrated in DaVinci’s painting Mona Lisa and his drawing Vitruvian Man.
Famous Buildings Influenced by Mathematical Principles
Here are some examples of famous buildings universally recognized for their beauty. We believe their architects used math and the principals of the Golden Section in their design:
Parthenon
The classical Doric columned Parthenon was built on the Acropolis between 447 and 432 BC. It was designed by the architects Iktinos and Kallikrates. The temple had two rooms to shelter a gold and ivory statue of the goddess Athena and her treasure. Visitors to the Parthenon viewed the statue and temple from the outside. The refined exterior is recognized for its proportional harmony which has influenced generations of designers. The pediment and frieze were decorated with sculpted scenes of Athena, the Gods, and heroes.

Parthenon Golden Section
Notre Dame Cathedral in Paris
Built on the Ile de la Cite, Notre Dame was built on the site of two earlier churches. The foundation stone was laid by Pope Alexander III in 1163. The stone building demonstrates various styles of architecture, due to the fact that construction occurred for over 300 years. It is predominantly French Gothic, but also has elements of Renaissance and Naturalism. The cathedral interior is 427 feet x 157 feet in plan. The two Gothic towers on the west façade are 223 feet high. They were intended to be crowned by spires, but the spires were never built. The cathedral is especially loved for its three stained glass rose windows and daring flying buttresses. During the Revolution, the building was extensively damaged and was saved from demolition by the emperor Napoleon.

Notre Dame Cathedral in Paris
Taj Mahal
Built in Agra between 1631 and 1648, the Taj Mahal is a white marble mausoleum designed by Ustad-Ahmad Lahori. This jewel of Indian architecture was built by Emperor Shah Jahan in memory of his favorite wife. Additional buildings and elements were completed in 1653. The square tomb is raised and is dramatically located at the end of a formal garden. On the interior, the tomb chamber is octagonal and is surrounded by hallways and four corner rooms. Building materials are brick and lime veneered with marble and sandstone.

Taj Mahal designed by Ustad-Ahmad Lahori
As you can see from the above examples, the application of mathematical principles can result in some pretty amazing architecture. The architects’ work reflects eye-catching harmony and balance. Although these buildings are all quite old, their designs have pleasing proportions which have truly passed the test of time.
https://bleckarchitects.com/math-in-architecture/
|
|
|
|
|
 Primer Primer
 Anterior
184 a 198 de 618
Siguiente Anterior
184 a 198 de 618
Siguiente Último
Último
|
|
| |
|
|
©2025 - Gabitos - Todos los derechos reservados | |
|
|

