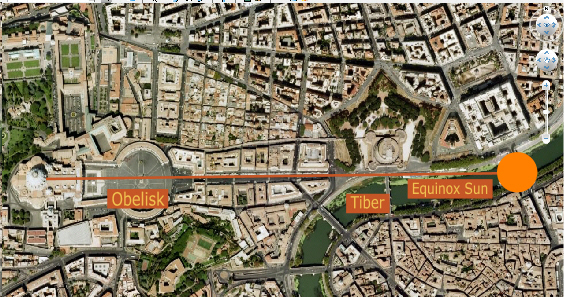
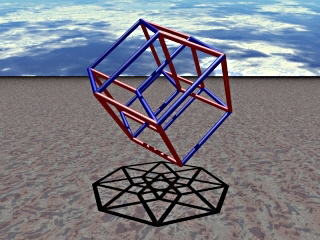
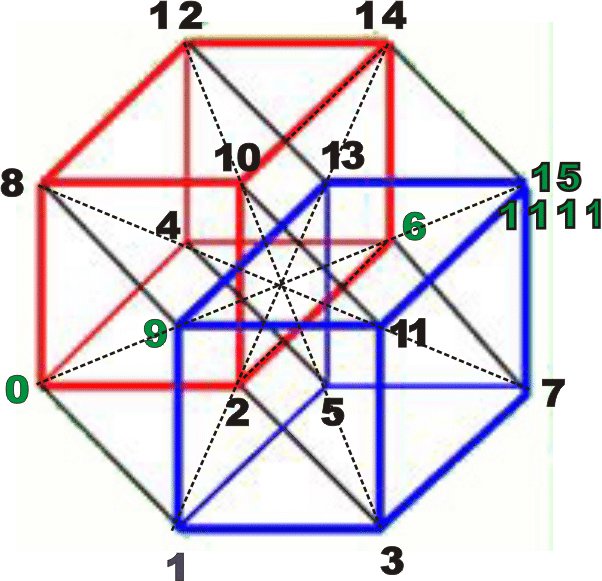
|
|
General: PLAZA DE SAN PEDRO (VATICANO)=HIPERCUBO ("MAQUINA DEL TIEMPO")
Elegir otro panel de mensajes |
|
|
|
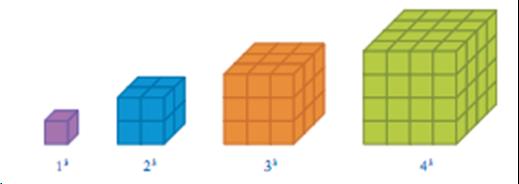
NÚMEROS CÚBICOS.
Los números cúbicos son aquellos que obtenemos al elevar al cubo los sucesivos números naturales:
13 = 1; 23 = 8; 33 = 27; .....
Pero también podemos construir estos números geométricamente,
|
|
|
es.walyou.com
2 Alcancia cubo Rubik
521 × 423 - 24k - jpg |
es.wikipedia.org
El interior de un cubo de
232 × 199 - 28k - jpg |
solostocks.com
Cubo Mágico
500 × 500 - 29k - jpg |
pocoseso.com
del Rubik - Cubo Magico -
450 × 338 - 28k - jpg |
Búsquedas relacionadas con cubo magico
EL MISMO "CUBO MAGICO" ES UN HIPERCUBO (HAY UN CUBO MAS CHICO EN EL CENTRO DEL MISMO)
| Reply |
Message 24 of 24 on the subject |
|
El término cuarta dimensión aparece en diversos contextos como la física, las matemáticas y la ciencia ficción. En cada contexto el significado es diferente:
En física, se hace referencia a la cuarta dimensión al hablar del tiempo, principalmente desde el planteamiento de la Teoría de la Relatividad.
En matemática, el concepto aparece asociado o bien a espacios euclídeos de más de tres dimensiones o, más generalmente, a espacios localmente euclídeos o 4-variedades diferenciables.
Hipercubo de 4 dimensiones espaciales girando, tal como se vería proyectado en el espacio tridimensional.
El interés en las dimensiones más altas alcanzó su clímax entre 1870 y 1920.1 En esos años se convirtió en tema frecuente en la literatura fantástica, el arte e incluso algunas teorías científicas. La cuarta dimensión, entendida como dimensión espacial adicional (no como dimensión temporal, como en la teoría de la relatividad) apareció en las obras literarias de Oscar Wilde, Fiódor Dostoyevski, Marcel Proust, H. G. Wells y Joseph Conrad, inspiró algunas obras musicales de Alexander Scriabin, Edgar Varèse y George Antheil y algunas obras plásticas de Pablo Picasso y Marcel Duchamp influyendo en el desarrollo del cubismo. Incluso personajes tan diversos como el psicólogo William James, la escritora Gertrude Stein o el socialista revolucionario Vladimir Lenin se interesaron en el tema.
Igualmente los matemáticos habían estado interesados en el tema al tratar de generalizar los conceptos de la geometría euclídea tridimensional. El matemático Charles L. Dodgson, que enseñó en la Universidad de Oxford, deleitó a generaciones de escolares escribiendo libros, bajo el pseudónimo de Lewis Carroll, que incorporaban algunas ideas sobre la cuarta dimensión. Desde el punto de vista académico, el estudio general de la geometría de la cuarta dimensión en gran parte resultado de los trabajos de Bernhard Riemann. Charles Howard Hinton, matemático y escritor de ciencia ficción británico, acuñó muchos neologismos para describir elementos en la cuarta dimensión. De acuerdo con el Oxford English Dictionary, fue el primero en emplear la palabra tesseract en su libro Una nueva era del pensamiento. También inventó las palabras “kata” (del griego “abajo”) y “ana” (del griego “arriba”) para describir las dos direcciones opuestas en la cuarta dimensión, equivalentes a derecha-izquierda, arriba-abajo, y adelante-atrás.
Los trabajos matemáticos sobre geometrías multidimensionales y geometrías no euclídeas habían sido considerado por los físicos como simples abstracciones matemáticas hasta que Henri Poincaré probó que el grupo de transformaciones de Lorentz que dejaban invariantes las ecuaciones del electromagnetismo podían ser interpretadas como "rotaciones" en un espacio de cuatro dimensiones. Más tarde, los trabajos de Einstein y la interpretación geométrica de estos por parte de Hermann Minkowski llevaron a la aceptación de la cuarta dimensión como una descripción necesaria para explicar los hechos observados relacionados con el electromagnetismo. Sin embargo, aquí la "cuarta dimensión" no era un lugar separado del espacio tridimensional (como en varias de las obras de ficción de la época) ni tampoco una dimensión espacial análoga a las otras tres dimensiones espaciales, sino una dimensión temporal que sólo puede recorrerse hacia el futuro. En la teoría general de la relatividad el campo gravitatorio es explicado como un efecto geométrico de la curvatura de un espacio-tiempo de cuatro dimensiones.
Más tarde, la teoría de Kaluza-Klein propuso que no sólo el campo gravitatorio podía ser interpretado de forma más sencilla como curvatura de un "espacio" de más de tres dimensiones, sino que si se introducía una nueva dimensión espacial enrollada o «compactificada», también el campo electromagnético podía ser interpretado como un efecto geométrico de la curvatura de dimensiones superiores. Así, la Kaluza proponía una teoría de campo unificado del electromagnetismo y la gravedad en un espacio-tiempo de cinco dimensiones, con una dimensión temporal, tres dimensiones espaciales extendidas y una dimensión espacial «compactificada» adicional, que, debido a su condición de compactificada, no era directamente visible pero su efecto era perceptible en forma de campo electromagnético.
Un ángulo recto se describe como un cuarto de una revolución. La Geometría Cartesiana escoge direcciones ortogonales arbitrariamente a través del espacio, lo que significa que cada dirección está en ángulo recto con las demás. Las 3 dimensiones ortogonales del espacio se conocen como altitud, longitud y latitud. La Cuarta Dimensión por lo tanto es la dirección en el espacio con ángulo recto a las 3 direcciones observables.
Un vector espacial es un conjunto de vectores, los cuales podemos imaginarlos como flechas, que proviene de un simple lugar llamado origen (vectores geométricos), que apuntan a otros lugares.
Un punto es un objeto de cero dimensiones. No tiene extensión en el espacio ni propiedades, como una flecha pero sin longitud. Este vector es llamado el vector cero y es el más simple vector espacial.
Una línea es un objeto unidimensional. Si escogemos un cierto vector distinto a cero en una cierta dirección, este vector tiene cierta longitud definida. Ese vector tiene una cabeza en un cierto punto en espacio y una cola en el origen. Si pensamos en estirar que ese vector así sea dos veces su largo, tres veces, etcétera y uniformemente, tomando todas las longitudes posibles (incluso la longitud cero, conseguir el vector cero), conseguiremos una sola línea con una sola dimensión: La de la longitud. Todos los vectores que describen puntos en esta línea serían paralelos. Aunque para visualizar la línea es necesario que ésta tenga un ancho mínimo, sin embargo, una línea de 1D no la tendría.
Un plano es un objeto de dos dimensiones. Tiene longitud y anchura pero no profundidad - algo como una hoja de papel, o más exactamente algo como las imágenes en un televisor común. El pensamiento en un plano en términos de vectores puede ser un poco más desafiante. Si pensamos en tomar un vector y lo movemos de modo que su cola esté tocando la cabeza del primero y esté formando un vector con su cola en el origen y la cabeza en la cabeza del segundo vector colocado de nuevo, tenemos una manera razonable de hablar de vectores de adición. Si tenemos dos vectores que no sean paralelos, podemos hablar de todos los puntos que podemos alcanzar por o solamente el estirar o ningunos de los vectores, y, agregando estos vectores juntos, estos puntos forman un plano.
El espacio, como lo percibimos, es tridimensional. Podemos pensar en poner una línea junto con un plano. Estas líneas son como un emparedado. Para conseguir a un cierto punto en espacio, podemos imaginarnos el viajar encima de la línea y después el movernos a través del plano al punto. Entonces tenemos tres vectores a pensar alrededor, uno a viajar una cierta distancia encima de la línea y dos para conseguir a un cierto punto en espacio.
Para tres rectas ortogonales en el espacio tridimensional (x, y y z) existe una cuarta, normal al espacio, ortogonal a estas tres rectas, que forma un eje p. ej. w.
El producto vectorial es la determinante de una matriz 4×4, donde una de las filas (o columnas) son los vectores unitarios h, i, j y k y las demás (filas o columnas respectivamente) están formadas por las componentes de tres vectores cuadradimensionales cualesquiera, este producto nos dará un cuarto vector perpendicular a estos tres mismos.
La Geometría euclidiana prevé una mayor variedad de formas para existir que en tres dimensiones. Los poliedros tridimensionales son recintos espaciales hechos de caras de dos dimensiones conectadas, los policronos cuadridimensionales son recintos del espacio cuadridimensional hechos de poliedros tridimensionales. Donde en tres dimensiones, hay exactamente cinco poliedros regulares, o los sólidos platónicos, que pueden existir, seis policronos regulares existen en la cuarta dimensión. Cinco de los seis se pueden interpretar como extensiones naturales de los sólidos platónicos, así como el cubo, un sólido platónico, es una extensión del cuadrado de dos dimensiones. El pentachoron está hecho de 5 tetraedros para las caras y 10 caras triangulares, y es el análogo cuadridimensional del tetraedro. El teseracto, o el hipercubo, se compone de 8 caras cúbicas y de 24 cuadrados, y es el politopo cuadridimensional medido. Los teseractos se doblan, la 16-celdas, son el equivalente del octaedro, pues son ambos politopos de cruz. Los politopos de 120 celdas y los de 600 celdas se doblan de igual modo, y son análogos al dodecaedro y al icosaedro, respectivamente. El de 24 celdas es un policrono regular único y que no tiene ningún equivalente tridimensional. Apenas pues la esfera, o 2-esfera, es una superficie de dos dimensiones curvada compuesta de todos los puntos equidistantes de un punto central dado, en un espacio tridimensional, la 3-esfera, una clase de hiperesfera, es el espacio que contiene todos los puntos equidistantes a un punto central dado, en un espacio cuadridimensional. Cada sección transversal tridimensional de un 3-esfera es un 2-esfera.
La analogía dimensional se usa frecuentemente para comprender el salto de una dimensión (en este caso, la tercera dimensión) a una más alta (cuarta dimensión). La analogía dimensional consiste en resolver un problema en n + 1 dimensiones relacionándolo primero con un problema análogo de (n - 1) dimensión, vale decir, "una dimensión menos". E igualmente debe analizarse el caso de cómo se relaciona el problema en n con el de (n + 1) dimensiones, es decir, "una más".
Edwin Abbott Abbott en su libro Planilandia (Flatland) escribe sobre un "ser cuadrado" que vive en un mundo de dos dimensiones, como la superficie de un pedazo de papel. Este "cuadrado" se enfrenta a experimentos de un ser tridimensional. El ser tridimensional es percibido por el "cuadrado" como un ser aparentemente divino, ya que puede poner y quitar objetos de una caja fuerte sin romperla ni abrirla (moviéndolos a través de su tercera dimensión), ver todo desde de la perspectiva de dos dimensiones sea incluido detrás de las paredes (puesto que ve "sobre" Planilandia), y totalmente invisible para los habitantes de Planilandia, puesto que está "arriba" y una dimensión por arriba de las dos dimensiones en las que el cuadrado está atrapado. No obstante, el ser tridimensional podría manifestarse en el mundo de dos dimensiones, pero sólo parcialmente, si fuera una esfera, aparecería como una secuencia de círculos sucesivos "que cambian de tamaño" (intersecciones de la esfera con el plano de dos dimensiones). Aplicando analogía dimensional, uno puede deducir que el ser cuadridimensional sería capaz de hazañas similares de nuestra perspectiva tridimensional.
Rudy Rucker demuestra esto en su novela "Spaceland", en la cual el protagonista encuentra los seres cuadridimensionales que demuestran tales energías. Un uso útil de la analogía dimensional en visualizar la cuarta dimensión está en la proyección. Una proyección es una manera para representar un objeto (n+1)-dimensional en la n-dimensión. Por ejemplo, las pantallas de computadora son de dos dimensiones, y todas las fotografías de objetos tridimensionales son representadas en dos dimensiones puesto que la información de la tercera dimensión (o de la profundidad) no puede ser representada por la pantalla (si el observador se mueve, aleje o acerque, la imagen no cambiará). En este caso, la profundidad se quita y se substituye por la información indirecta. La retina del ojo es un arsenal de dos dimensiones de receptores pero puede permitir que el cerebro perciba la naturaleza de objetos tridimensionales usando la información indirecta (como la perspectiva, el sombreado, visión binocular, etc.).
La perspectiva del uso de los artistas da profundidad tridimensional a los cuadros de dos dimensiones. Asimismo, los objetos en la cuarta dimensión se pueden proyectar matemáticamente a las familiares tres dimensiones, donde pueden entonces ser examinados más convenientemente. En este caso, la "retina de un ojo cuadridimensional" tendría un arsenal de receptores tridimensionales. El ser hipotético con tal ojo percibiría la naturaleza de objetos cuadridimensionales usando la información indirecta contenida en las imágenes que recibe en su retina. La proyección de la perspectiva a partir de cuatro dimensiones produce efectos similares como en el caso tridimensional, tal como la perspectiva.
Esto agrega "profundidad cuadridimensional" a estos cuadros tridimensionales. La analogía dimensional también ayuda a entender tales proyecciones. Por ejemplo, los objetos de dos dimensiones son limitados por límites unidimensionales: un cuadrado es limitado por cuatro bordes o líneas. Los objetos tridimensionales son limitados por superficies de bidimensionales: un cubo es limitado por 6 cuadrados. Aplicando analogía dimensional, uno puede deducir que un cubo cuadridimensional, conocido como teseracto, es limitado por los volúmenes tridimensionales.
Y de hecho, éste es el caso matemáticamente: el teseracto es limitado por 8 cubos. Saber esto es indispensable para entender cómo interpretar una proyección tridimensional del teseracto. Los límites del teseracto proyectan a los volúmenes en la imagen, superficies no simplemente de dos dimensiones. Esto ayuda a entender las características de dichas dimensiones que de otra manera sólo confundirían. De igual manera, el concepto de sombras puede ayudarnos mejor a entender la teoría de cuatro dimensiones. Si usted proyectara una luz sobre objeto tridimensional, éste proyectaría una sombra de dos dimensiones. Por lo tanto la luz en un objeto de dos dimensiones echaría una sombra unidimensional (en un mundo de dos dimensiones), y la luz en un objeto unidimensional en un mundo unidimensional echaría una sombra cero-dimensional, es decir, un punto de la no-luz. Esta idea se puede utilizar en la otra dirección; la luz en un objeto cuadridimensional proyectaría una sombra tridimensional. Como ejemplo, la sombra de un cubo transparente, proyectaría una sombra sobre el papel, de dos cuadrados, unidos por sus vértices con 4 segmentos.
Semejantemente, si era un cubo cuadridimensional iluminado con luz de 4 dimensiones, su sombra sería la de un cubo tridimensional dentro de otro cubo tridimensional. Siendo tridimensionales podemos solamente ver el mundo con nuestros ojos en dos dimensiones; el ser cuadridimensional consideraría el mundo en tres. Así podría, por ejemplo, ver los seis lados de una caja opaca simultáneamente. No solamente eso; también podría ver lo que hay al interior de la caja, como en Planilandia, en donde la esfera ve objetos en el mundo de dos dimensiones y todo dentro de ellos simultáneamente. Análogo, un espectador cuadridimensional vería todos los puntos en nuestro espacio tridimensional simultáneamente, incluyendo la estructura interna de objetos sólidos y de cosas obscurecidos de nuestro punto de vista.
Albert Einstein en su célebre teoría de 1905 de la relatividad especial habló por primera vez del tiempo como una cuarta dimensión y como algo indispensable para ubicar un objeto en el espacio y en un momento determinado. El tiempo en la teoría de la relatividad no es una dimensión espacial más, ya que fijado un punto del espacio-tiempo éste puede ser no alcanzable desde nuestra posición actual, hecho que difiere de la concepción usual de dimensión espacial. Aunque inicialmente se interpretó el tiempo como una "dimensión" matemática necesaria para ubicar un evento u objeto, en la teoría de la relatividad general el tiempo es tratado como una dimensión geométrica más, aunque los objetos materiales no puedan seguir una trayectoria completamente arbitraria a lo largo del tiempo (como por ejemplo "dar la vuelta" y viajar al pasado). La necesidad del tiempo dentro de la teoría de la relatividad es necesaria por dos motivos:
En primer lugar, los objetos no sólo se mueven a través del espacio sino que también lo hacen a través del tiempo, es decir su coordenada temporal aumenta continuamente, por lo que hubo la necesidad de hablar del tiempo ligado al espacio como la cuarta dimensión (en inglés spacetime, en castellano espacio-tiempo). Además el ritmo de avance en la dimensión temporal depende del estado de movimiento del observador, produciéndose una dilatación temporal efectiva para los observadores más rápidos en relación al tiempo medido por un observador estacionario.
En segundo lugar, el carácter intrínseco del espacio-tiempo y su cuatridimensionalidad requiere un modo conceptualmente diferente de tratar la geometría del universo, puesto que una cuarta dimensión implica un espacio plano (bidimensional) que se curva en la teoría de la relatividad general por la acción de la gravedad de la materia originándose la curvatura del espacio-tiempo.
Finalmente cabe añadir que algunas teorías físicas como la teoría de Kaluza-Klein y las teoría de supercuerdas, en sus varias versiones, añaden a las tres dimensiones físicas espaciales entre 1 y 9 dimensiones espaciales adicionales, de tipo compacto; además de la dimensión temporal.
|
|
|
|
|
|
|
|
|
| Reply |
Message 119 of 121 on the subject |
|
|
The TABERNACLE
|
|
| Reply |
Message 120 of 121 on the subject |
|
|
|
| Reply |
Message 121 of 121 on the subject |
|
|
CONEXION DE LA MANZANA (ESTRELLA DE 5 PUNTAS=NUMERO PHI= 1.618033..) CON EL RELOJ (GEMATRIA DE PHI EN INGLES ES 33)
klockit.com
6" Star of David Theme Clock
750 × 735 - 65k - jpg |
amazon.com
STAR OF DAVID Wall Clock
355 × 355 - 34k - jpg |
cafepress.com
Star of David Wall Clock
225 × 225 - 12k - jpg |
amazon.com
Wall Clock Blue Star of David
1000 × 1000 - 84k - jpg |
|
|
|
54. Job 33:33 Y si no, óyeme tú a mí;
Calla, y te enseñaré sabiduría.
666= SISTEMA SEXAGECIMAL= RELOJ
|
| Reply |
Message 3 of 3 on the subject |
|
|
54. Job 33:33 Y si no, óyeme tú a mí;
Calla, y te enseñaré sabiduría.
666= SISTEMA SEXAGECIMAL= RELOJ
|
|
|
|
|
|
|
|
|
|
|
|
| Reply |
Message 20 of 20 on the subject |
|
|
|
|
|
|
|
|
Génesis 7
1. Dijo luego Jehová a Noé: Entra tú y toda tu casa en el arca; porque a ti he visto justo delante de mí en esta generación.
2. De todo animal limpio tomarás siete parejas, macho y su hembra; mas de los animales que no son limpios, una pareja, el macho y su hembra.
3. También de las aves de los cielos, siete parejas, macho y hembra, para conservar viva la especie sobre la faz de la tierra.
4. Porque pasados aún siete días, yo haré llover sobre la tierra cuarenta días y cuarenta noches; y raeré de sobre la faz de la tierra a todo ser viviente que hice.
5. E hizo Noé conforme a todo lo que le mandó Jehová.
6. Era Noé de seiscientos años cuando el diluvio de las aguas vino sobre la tierra.
7. Y por causa de las aguas del diluvio entró Noé al arca, y con él sus hijos, su mujer, y las mujeres de sus hijos.
8. De los animales limpios, y de los animales que no eran limpios, y de las aves, y de todo lo que se arrastra sobre la tierra,
9. de dos en dos entraron con Noé en el arca; macho y hembra, como mandó Dios a Noé.
10. Y sucedió que al séptimo día las aguas del diluvio vinieron sobre la tierra.
11. El año seiscientos de la vida de Noé, en el mes segundo, a los diecisiete días del mes, aquel día fueron rotas todas las fuentes del grande abismo, y las cataratas de los cielos fueron abiertas,
EN EL CONTEXTO A LA LUNA NUEVA EN LUNA LLENA, EL DIECISIETE NOS CAE EN LUNA CRECIENTE.
12. y hubo lluvia sobre la tierra cuarenta días y cuarenta noches.
13. En este mismo día entraron Noé, y Sem, Cam y Jafet hijos de Noé, la mujer de Noé, y las tres mujeres de sus hijos, con él en el arca;
14. ellos, y todos los animales silvestres según sus especies, y todos los animales domesticados según sus especies, y todo reptil que se arrastra sobre la tierra según su especie, y toda ave según su especie, y todo pájaro de toda especie.
15. Vinieron, pues, con Noé al arca, de dos en dos de toda carne en que había espíritu de vida.
16. Y los que vinieron, macho y hembra de toda carne vinieron, como le había mandado Dios; y Jehová le cerró la puerta.
17. Y fue el diluvio cuarenta días sobre la tierra; y las aguas crecieron, y alzaron el arca, y se elevó sobre la tierra.
18. Y subieron las aguas y crecieron en gran manera sobre la tierra; y flotaba el arca sobre la superficie de las aguas.
19. Y las aguas subieron mucho sobre la tierra; y todos los montes altos que había debajo de todos los cielos, fueron cubiertos.
20. Quince codos más alto subieron las aguas, después que fueron cubiertos los montes.
21. Y murió toda carne que se mueve sobre la tierra, así de aves como de ganado y de bestias, y de todo reptil que se arrastra sobre la tierra, y todo hombre.
22. Todo lo que tenía aliento de espíritu de vida en sus narices, todo lo que había en la tierra, murió.
23. Así fue destruido todo ser que vivía sobre la faz de la tierra, desde el hombre hasta la bestia, los reptiles, y las aves del cielo; y fueron raídos de la tierra, y quedó solamente Noé, y los que con él estaban en el arca.
24. Y prevalecieron las aguas sobre la tierra ciento cincuenta días.
|
| Reply |
Message 58 of 58 on the subject |
|
Génesis 8
1. Y se acordó Dios de Noé, y de todos los animales, y de todas las bestias que estaban con él en el arca; e hizo pasar Dios un viento sobre la tierra, y disminuyeron las aguas.
2. Y se cerraron las fuentes del abismo y las cataratas de los cielos; y la lluvia de los cielos fue detenida.
3. Y las aguas decrecían gradualmente de sobre la tierra; y se retiraron las aguas al cabo de ciento cincuenta días.
4. Y reposó el arca en el mes séptimo, a los diecisiete días del mes, sobre los montes de Ararat.
5. Y las aguas fueron decreciendo hasta el mes décimo; en el décimo, al primero del mes, se descubrieron las cimas de los montes.
6. Sucedió que al cabo de cuarenta días abrió Noé la ventana del arca que había hecho,
7. y envió un cuervo, el cual salió, y estuvo yendo y volviendo hasta que las aguas se secaron sobre la tierra.
8. Envió también de sí una paloma, para ver si las aguas se habían retirado de sobre la faz de la tierra.
9. Y no halló la paloma donde sentar la planta de su pie, y volvió a él al arca, porque las aguas estaban aún sobre la faz de toda la tierra. Entonces él extendió su mano, y tomándola, la hizo entrar consigo en el arca.
10. Esperó aún otros siete días, y volvió a enviar la paloma fuera del arca.
11. Y la paloma volvió a él a la hora de la tarde; y he aquí que traía una hoja de olivo en el pico; y entendió Noé que las aguas se habían retirado de sobre la tierra.
12. Y esperó aún otros siete días, y envió la paloma, la cual no volvió ya más a él.
13. Y sucedió que en el año seiscientos uno de Noé, en el mes primero, el día primero del mes, las aguas se secaron sobre la tierra; y quitó Noé la cubierta del arca, y miró, y he aquí que la faz de la tierra estaba seca.
14. Y en el mes segundo, a los veintisiete días del mes, se secó la tierra. (AQUI ESTA LA CLAVE MATEMATICA DEL "EXPERIMENTO FILADELFIA" EN EL CONTEXTO AL "ARCA DE NOE". 2/27 EN UN MARCO AL CALENDARIO LUNAR. ESTO EXPLICA LA FUERTE CONNOTACION MARITIMA DEL MISMO. ES QUE EN REALIDAD EL "ARCA DE NOE" TAMBIEN TIENE FUERTE CONNOTACION CON EL "AGUJERO DE GUSANO".)
15. Entonces habló Dios a Noé, diciendo:
16. Sal del arca tú, y tu mujer, y tus hijos, y las mujeres de tus hijos contigo.
17. Todos los animales que están contigo de toda carne, de aves y de bestias y de todo reptil que se arrastra sobre la tierra, sacarás contigo; y vayan por la tierra, y fructifiquen y multiplíquense sobre la tierra.
18. Entonces salió Noé, y sus hijos, su mujer, y las mujeres de sus hijos con él.
19. Todos los animales, y todo reptil y toda ave, todo lo que se mueve sobre la tierra según sus especies, salieron del arca.
20. Y edificó Noé un altar a Jehová, y tomó de todo animal limpio y de toda ave limpia, y ofreció holocausto en el altar.
21. Y percibió Jehová olor grato; y dijo Jehová en su corazón: No volveré más a maldecir la tierra por causa del hombre; porque el intento del corazón del hombre es malo desde su juventud; ni volveré más a destruir todo ser viviente, como he hecho.
22. Mientras la tierra permanezca, no cesarán la sementera y la siega, el frío y el calor, el verano y el invierno, y el día y la noche.
Noten la clave NUMERO OCHO Y EL NUMERO CUATRO, EL MISMO PATRON DEL VATICANO.
Do you notice the symbolic 8 rays within the circle? Symbolic of the star Sirius.
LA MISMA PIRAMIDE DEL VATICANO, AL ESTAR DISEÑADA EN FUNCION A SIRIO, Y A SU NEXO CON EL ESTE, OESTE, NORTE Y SUR, OSEA LAS CUATRO ORIENTACIONES, ES UNA REFERENCIA A LA "MAQUINA DEL TIEMPO". POR ESA CAUSA ESTA ADENTRO DE LA CERRADURA Y TIENE RELACION CON LA LLAVE DE DAVID "EXPERIMENTO FILADELFIA".
2. Isaías 22:22: Y pondré la LLAVE de la casa de David sobre su hombro; y abrirá, y nadie cerrará; cerrará, y nadie abrirá.
3. Mateo 16:19: Y a ti te daré las LLAVEs del reino de los cielos; y todo lo que atares en la tierra será atado en los cielos; y todo lo que desatares en la tierra será desatado en los cielos.
4. Lucas 11:52: ¡Ay de vosotros, intérpretes de la ley! porque habéis quitado la LLAVE de la ciencia; vosotros mismos no entrasteis, y a los que entraban se lo impedisteis.
5. Apocalipsis 1:18: y el que vivo, y estuve muerto; mas he aquí que vivo por los siglos de los siglos, amén. Y tengo las LLAVEs de la muerte y del Hades.
6. Apocalipsis 3:7: Escribe al ángel de la iglesia en Filadelfia: Esto dice el Santo, el Verdadero, el que tiene la LLAVE de David, el que abre y ninguno cierra, y cierra y ninguno abre:
EL DIA Y LA NOCHE ES UNA REFERENCIA A LAS 24 HORAS, OSEA A LA SANTA CENA.
DIA / SOL/ HOMBRE / ORO / PAN / CUADRADO
NOCHE / LUNA/ MUJER / PLATA / VINO / CIRCULO
HECHOS 12:12 (JUAN MARCOS ES EL GRIAL)
|
|
|
|
|
|
|
Washington DC: el Monumento a Washington = 8 y estrella octágono - la diosa sumeriana Inanna
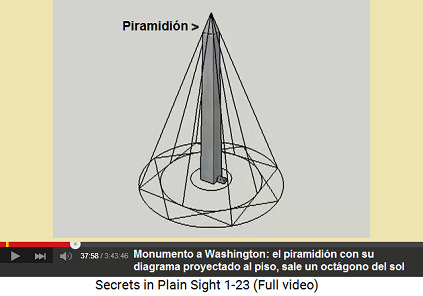 Monumento a Washington: el piramidión con su diagrama proyectado al piso, sale un octágono del sol
Bernard I. Pietsch detectó: las líneas alargadas de la pirámide de la punta (del piramidión pequeño) provocan un diagrama secreto en el piso con una estrella octagonal (38min.15seg.). Una estrella octagonal es el símbolo de la diosa sumeriana Inanna, la base de todas las leyendas de Isis (38min.29seg.). La civilización sumeriana fue solo detectada en 1890 (38min.42seg.). Así la ciencia esotérica ha ordenado todo a Isis lo que es en realidad conectado con Inanna (38min.48seg.).
Simbolismo de estrella de octagrama en todo el mundo
-- estrella de la diosa hindú Laksmí (39min.10seg.)
-- el grupo de 8 dioses de Egipto que forman la "ogdóada de Hermopolis" (Amun, Kauket, Amaunet, Hauhet, Naunet, Heh, Nun, Kuk, con el "huevo cósmico" en el centro con el dios solar Ra) (39min.19seg., 1h29min.36seg.).
-- calendario celta (39min.23seg.)
-- gnosticismo valentiano que convierta conceptos de Egipto en conceptos cristianos (39min.29seg.)
-- rueda budista de Dharma (39min.39seg.)
-- octagrama islámico: Rub el Hizb (39min.45seg.)
-- la iglesia ortodoxa también usa estrellas octagramas: Christ Pantocrater (39min.59seg.)
-- la piedra del calendario azteca en México (40min.7seg.)
-- el Vaticano [criminal satanista gay] usa el octágono en su patio y también usa un obelisco como pene en su centro [!] lo que trabaja como reloj solar (40min.23seg.).
En total la estrella de octagrama es un símbolo solar (40min.35seg.).
Monumento de Washington: mediciones de los órganos sexuales femeninos - y la Gran Pirámide de Guiza
La energía femenina del Monumento a Washington es representada con las líneas de un pez "vesica piscis" (40min.46seg.) que representan las piernas de una mujer con su vulva (41min.5seg.). Cuando los círculos de un pez de círculos (vesica piscis) son agrandados hasta al diámetro de la altura del obelisco (sale un diámetro de 555' (pies)) así la Gran Pirámide de Guiza sale exactamente en esa "vulva" (41min.6seg.) con una altura de 481 y 1/11 pies (481'+1/11') (41min.13seg.). Qué coincidencia. El arquitecto del Monumento a Washington debe haber tenido conexiones con los pirámides de Egipto (41min.16seg.).
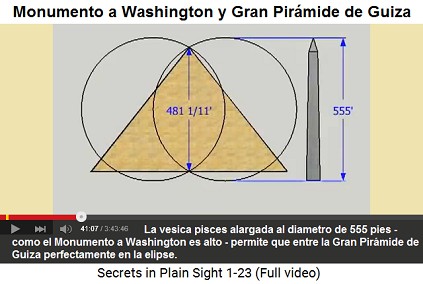 La elipse de pez agrandada del Monumento a Washington a un diámetro de 555' (pies) permite que la Gran Pirámide de Guiza entre perfectamente en esa elipse.
Las proporciones de la Gran Pirámide de Egipto y del obelisco del Monumento a Washington tienen una conexión directa:
-- altura del obelisco del Monumento a Washington (555') = largo inclinado de la Gran Pirámide (555') (41min.20seg.)
-- radio del piramidión proyectado al piso = medio radio de la Gran Pirámide (41min.20seg.)
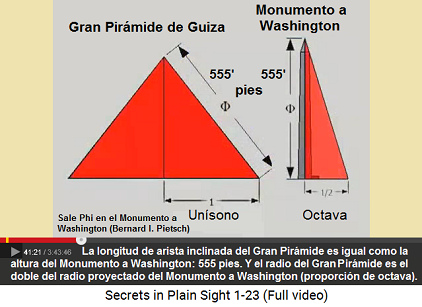 Esquema: el largo inclinado de la Gran Pirámide de Guiza es la altura del Monumento a Washington (555 pies), y el radio de la Gran Pirámide es el doble del radio proyectado del piramidión del Monumento a Washington
Washington DC: el patio trasero de la Casa Blanca es como Stonehenge
El patio trasero de la Casa Blanca tiene la misma forma de "U" como la estructura interior de Stonehenge (41min.43seg.).
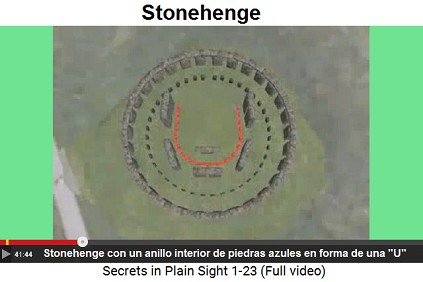  El patio trasero de la Casa Blanca está en forma de una "U" como Stonehenge tiene - Stonehenge con un anillo interior de piedras azules en forma de una "U"
Y los dos triángulos alrededor de la Casa Blanca forman un rectángulo de 5:12 (41min.50seg.). Esas proporciones son las mismas como el rectángulo de piedras de estaciones (41min.53seg.).
  La Casa Blanca con una "U" y triángulos con proporciones 5:12 - Stonehenge con una "U" y con el triángulo de estaciones 5:12 [Conclusión: La Casa Blanca es otro Stonehenge y extraterrestres de Stonehenge están gobernando la Casa Blanca].
Una línea directa de la punta del "Triángulo Federal" de Washington DC al centro de Stonehenge en Inglaterra nos muestra que la línea cruce el Parque Central de Nueva York (42min.9seg.) precisamente en otro ángulo con la proporción de 5:12 (42min.27seg.).
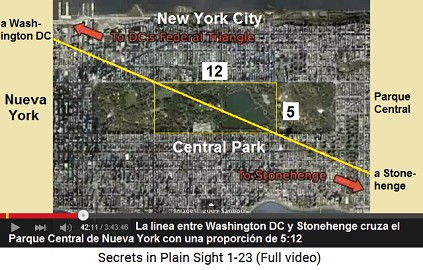  Línea directa de Washington a Stonehenge - La línea entre Washington DC y Stonehenge cruza el Parque Central de Nueva York con una proporción de 5:12 |
|
|
|
|
Sólido de Kepler-Poinsot
Los sólidos de Kepler-Poinsot con sus símbolos de Schläfli.
Un sólido de Kepler (también llamado sólido de Kepler-Poinsot) es un poliedro regular no convexo, cuyas caras son todas polígonos regulares y que tiene en todos sus vértices el mismo número de caras concurrentes (compárese con los sólidos platónicos).
Existen sólo cuatro tipos, con las denominaciones siguientes:
Las caras están solo parcialmente en la superficie del sólido, y las partes expuestas están sólo conectadas en puntos (si están conectadas de algún modo). Si las partes se cuentan como caras separadas, el sólido deja de ser regular.
Características
Un sólido de Kepler cubre su esfera circunscrita más de una vez (con una esfera interior y otra exterior), con los centros de las caras como puntos direccionales en los sólidos que tienen caras en forma de pentagrama, mientras que en los otros son los vértices los que cumplen esa función. Por esta razón, no son necesariamente equivalentes topológicos de la esfera como lo son los sólidos platónicos, y en particular la característica de Euler V − E + F = 2 se verifica solamente para el Gran dodecaedro estrellado y para el Gran icosaedro.
Esto dependerá de cómo se observe el poliedro. Considérese, por ejemplo, el pequeño dodecaedro estrellado.1 Consiste en un dodecaedro con una pirámide pentagonal en cada una de sus 12 caras. En consecuencia, las 12 caras se extienden a pentagramas con el pentágono central dentro del sólido. La parte externa de cada cara consiste en cinco triángulos conectados por sólo cinco puntos. Si se cuentan separadamente, hay 60 caras (pero estas son triángulos isósceles que no son polígonos regulares, en cuyo caso seria un pentaquisdodecaedro). De modo similar, cada lado puede ser contado como tres, pero entonces los habrá de dos tipos. Igualmente, con los "cinco puntos" antes mencionados: en total habrá 20 puntos que pueden contarse como vértices, por lo que habrá un total de 32 vértices (otra vez, de dos tipos). Ahora la ecuación de Euler se verifica: 60 - 90 + 32 = 2.
Tipos
Hay cuatro sólidos de Kepler distintos:
Los dos primeros son estrellamientos, es decir, sus caras son convexas. Los otros dos tienen caras cóncavas, pero cada par de caras que se encuentra en un vértice de hecho lo hace en dos.
Historia
Mosaico del suelo en la basílica de San Marcos, a veces atribuido a Paolo Uccello.
La mayoría de los poliedros de Kepler-Poinsot, si no todos, eran ya conocidos de una forma u otra antes de Kepler. Un pequeño dodecaedro estrellado aparece en una tarsia de mármol (panel de incrustaciones) en el suelo de la basílica de San Marcos de Venecia, Italia. Data del siglo XV y, a veces se atribuye a Paolo Uccello. Wenzel Jamnitzer, en su obra Perspectiva corporum regularium (Perspectivas de los sólidos regulares), un libro de grabados en madera publicado en el siglo XVI, representa el gran dodecaedro y el gran dodecaedro estrellado.2 Se desprende de la disposición general del libro que consideraba solamente los cinco sólidos platónicos como regulares, y no comprendía la naturaleza periódica de sus grandes dodecaedros.
El pequeño y gran dodecaedro estrellado, a veces llamados poliedros de Kepler, fueron reconocidos por primera vez como regulares por Johannes Kepler en 1619, cuando notó que los dodecaedros estrellados (tanto el grande como el pequeño) se componían de dodecaedros "ocultos" (con caras pentagonales) que tienen caras compuestas de triángulos, tomando la apariencia de estrellas estilizadas. Los obtuvo por estelación del dodecaedro regular convexo, por primera vez, tratándolo como una superficie en lugar de un sólido. Se dio cuenta de que extendiendo los bordes o caras del dodecaedro convexo hasta que se encontrasen de nuevo, se podían obtener pentágonos estrellados. De esta manera construyó los dos dodecaedros estrellados, cada uno con la región convexa central de cada cara "oculta" en el interior, sólo con los brazos triangulares visibles. El paso final de Kepler fue reconocer que estos poliedros se ajustaban a la definición de regularidad, aunque fueran cóncavos en lugar de convexos, como sí lo eran los tradicionales sólidos platónicos.
En 1809, Louis Poinsot redescubrió las figuras de Kepler, mediante el ensamblaje de pentágonos estrellados alrededor de cada vértice. También montó polígonos convexos alrededor de los vértices de las estrellas para descubrir dos estrellas más regulares, el gran icosaedro y el gran dodecaedro. Por ello, algunos llaman a estos dos los poliedros de Poinsot. Poinsot no sabía si había descubierto todos los poliedros regulares estrellados.
Tres años más tarde, Augustin Cauchy demostró que la lista por estelación de los sólidos platónicos estaba completa, y casi medio siglo después, en 1858, Joseph Louis François Bertrandproporcionó una prueba más elegante por facetado de ellas.
Al año siguiente, Arthur Cayley dio a los poliedros de Kepler–Poinsot los nombres por los que generalmente conocidos hoy.
Unos cien años más tarde, John Conway desarrolló una terminología sistemática para las estelaciones hasta un máximo de cuatro dimensiones. Dentro de este esquema, sugirió nombres ligeramente modificados para dos de los poliedros regulares estrellados. Los nombres de Conway han sido considerados de utilidad, pero no han sido ampliamente adoptados.
| Nombre de Cayley |
pequeño dodecaedro estrellado |
gran dodecaedro |
gran dodecaedro estrellado |
gran icosaedro |
| Nombre de Conway |
dodecaedro estrellado |
gran dodecaedro (sin cambio) |
dodecaedro grande estrellado |
gran icosaedro (sin cambio) |
https://es.wikipedia.org/wiki/S%C3%B3lido_de_Kepler-Poinsot |
|
|
 First Previous 2 to 5 of 5 Next  Last |
|
|
Posted in Azulejos-Mosaicos, Italia, Templo with tags Poliedros on 7 junio 2012 by angelrequena
Hace tiempo hablamos del conocido pequeño dodecaedro estrellado del pavimento de la puerta de salida derecha del duomo de San Marcos. No es el único de la catedral veneciana: apenas visible para la visita ordinaria hay otro más pequeño, justo debajo del iconostasio en su centro, en lugar preferente y en línea con el altar.
Si se entra hacia la Pala de Oro puede verse una mancha central en la lejanía pero casi sin distinguirse. En mi última visita tuve la gran suerte de encontrar un ordenanza amable que encendía las luces a un grupo concertado que me permitió verlo y fotografiarlo. No desmerece de su hermano mayor, si cabe revela mayor virtuosismo y ostentación del dominio de la perspectiva matemática.
Hay cuatro sólidos regulares cóncavos, los dos de Poinsot y los dos de Kepler. Venecia nos ofrece los dos de Kepler en San Pantaleone y uno en San Marcos pero en dos lugares, uno alejado para despedirse del templo y otro en el lugar más destacado: la entrada central al recinto más sagrado.
El dodecaedro estrellado de la puerta (abajo) solo tiene una corona de taracea marmórea complementaria mientras que el del iconostasio (arriba) tiene tres.
3 Comments »
https://mateturismo.wordpress.com/tag/poliedros/page/7/
|
|
|
|
|
|
|
|
 
LLAVE DE ORO Y DE PLATA AL IGUAL QUE LA MANZANA
LAS MATEMATICAS SON EXACTAS.
GLORIA A DIOS TODOPODEROSO. QUE BELLAS SON LAS MATEMATICAS
MATEO
16:18 Y yo también te digo, que tú eres Pedro, y sobre esta roca edificaré mi iglesia; y las puertas del Hades no prevalecerán contra ella. (NUMERO DE ORO) (MARIA MAGDALENA SIMBOLIZA A LA IGLESIA/NUEVA JERUSALEM. AQUI NUESTRO SEÑOR INDUDABLEMENTE BUSCA UN NEXO ESOTERICO CON SU ESPOSA Y EL GRIAL-S-OPHI-A/SABIDURIA-ONE EN EL BILLETE DE UN DOLAR ES UN ANAGRAMA DE NOE)
El Número de Oro; Phi; la Divina Proporción
MARY MAGDALENEEAGLE/DAN/M
16:19 Y a ti te daré las llaves del reino de los cielos; y todo lo que atares en la tierra será atado en los cielos; y todo lo que desatares en la tierra será desatado en los cielos.
EL TERMINO EDIFICARE EN MATEO 16:18 TIENE CONNOTACION, PARA UN JUDIO, EL TENER UN HIJO. CONCRETAMENTE NUESTRO SEÑOR JESUCRISTO ESTA INTERRELACIONANDO A LA IGLESIA CON JUAN MARCOS. EL MENSAJE DE JESUS AQUI ES QUE LA IGLESIA ES JUAN MARCOS.
JANO / JUAN /PUERTA / GATE / MARCO
H1129
בָּנָה baná; raíz prim.; construir (lit y fig.):-albañil, canterón, poner cimientos, construir, edificador, edificar, edificio, fabricar, fortificar, hacer, tener hijo, labrar, levantar, maestro, obra, poner, properar, reedificar, reparar, restablecer, restaurar.
http://shoffarchurch.globered.com/categoria.asp?idcat=21
TENER UN HIJO ES CONSTRUIR UNA CASA
 En el pensamiento tradicional judío, tener un hijo está asociado con construir una casa y levantar el nombre de la familia. En el Salmo (Tehilim) 2:6-7, el Mesías Regio judío es llamado el Hijo de Di-s, según está escrito:
-
"Yo he puesto mi rey sobre Sión, mi santo monte. Yo publicaré el decreto [uno de los pasos para la entronización del rey judío>; el Señor me ha dicho: Mi hijo eres tú; Yo te engendré hoy."
En Hechos 13:33, confirma el Salmo (Tehilim) 2:6-7 está hablando sobre el Mesías (Mashíaj) judío Yeshúa/Jesús, según está escrito:
-
"La cual Dios ha cumplido a los hijos de ellos, a nosotros, resucitando a Jesús; como está escrito también en el salmo segundo: Mi hijo eres tú, yo te he engendrado hoy."
En la Mikvá (inmersión/bautismo) del Mesías (Mashíaj) judío Yeshúa/Jesús, una voz (kol) del cielo habló a Yeshúa/Jesús y le llamó el Hijo de Di-s. En Mateo (Matityahu) 3:13, 16-17 está escrito:
-
"Entonces Jesús vino de Galilea a Juan [Yojanán el Inmersor> al Jordán, para ser bautizado por él…y Jesús, después que fue bautizado, subió luego del agua; y he aquí los cielos le fueron abiertos, y vio al Espíritu de Dios [Rúaj HaKódesh> que descendía como paloma, y venía sobre él. Y hubo una voz que decía: Este es mi Hijo amado [Salmo 2:7>, en quien tengo complacencia."
Una vez más, en el pensamiento tradicional judío, tener un hijo está asociado con construir una casa. Esta verdad se puede comprender de la lengua hebrea misma. La palabra hebrea para hijo es "ben." Es la palabra 1121 de Strong en la Concordancia Hebrea. Hijo o ben en hebreo significa "un hijo o constructor del nombre de la familia." Hijo o ben en hebreo viene de la palabra 1129 que es la palabra hebrea "Baná" que significa "construir." La palabra hebrea para casa es, beit, Es la palabra 1004 de Strong. La palabra hebrea para casa, beit, también viene de la palabra hebrea "baná" que significa "construir." Por lo tanto, la lengua hebrea nos comunica que tener un hijo está asociado con construir una casa o levantar el nombre de la familia. Esta verdad espiritual se puede ver en la Torá en el libro de Deuteronomio (Devarim) 25:5-9, según está escrito:
-
"Cuando hermanos habitaren juntos, y muriere alguno de ellos, y no tuviere hijo, la mujer del muerto no se casará fuera con hombre extraño; su cuñado se llegará a ella, y la tomará por su mujer, y hará con ella parentesco. Y el primogénito que ella diere a luz sucederá en el nombre de su hermano muerto, para que el nombre de éste no sea borrado de Israel. Y si el hombre no quisiere tomar a su cuñada, irá entonces su cuñada a la puerta, a los ancianos, y dirá: Mi cuñado no quiere suscitar nombre en Israel a su hermano; no quiere emparentar conmigo. Entonces los ancianos de aquella ciudad lo harán venir, y hablarán con él; y si él se levantare y dijere: No quiero tomarla, se acercará entonces su cuñada a él delante de los ancianos, y le quitará el calzado del pie, y le escupirá en el rostro, y hablará y dirá: Así será hecho al varón que no quiere edificar la casa de su hermano."
Se puede ver también en Rut 4:11 que tener un hijo está asociado con levantar una casa. Las dos madres terrenales de las dos casas de Israel Raquel y Lea, compitieron entre ellas sobre tener hijos para edificar la casa de Jacob. En Rut 4:11 está escrito:
-
"Y dijeron todos los del pueblo que estaban a la puerta con los ancianos: Testigos somos. El Señor haga a la mujer que entra en tu casa como a Raquel y Lea, las cuales edificaron la casa de Israel; y tú seas ilustre en Efrata, y seas de renombre en Belén."
http://www.hebroots.com/2casach6.html
-
1 Pedro 5:13: La iglesia que está en Babilonia, elegida juntamente con vosotros, y Marcos mi HIJO, os saludan.
Cuando PEDRO aqui le llama a MARCOS mi HIJO es una obvia simbologia espiritual a un hipotetico PADRINAZGO DE PEDRO SOBRE JUAN MARCOS. ¿La denominacion hacia el PAPADO de la IGLESIA CATOLICA como SANTO PADRE tiene este origen?
LA CLAVE DEL EXPERIMENTO FILADELFIA
SAR (PRINCIPE)= LETRA S= SABIDURIA (SABADO)= SERPIENTE= $= RIO NILO (FORMA DE SERPIENTE)= RIO TIBER (FORMA DE SERPIENTE)
Jano o Janus era un antiguo dios solar asirio-babilónico, asimilado primero como dios principal por los etruscos y luego por los romanos. Su principal característica es la de tener dos caras, una cara mirando a cada lado, una hacia atrás mirando al pasado y otra hacia adelante mirando al futuro, pues era el que vigilaba el umbral que los separa. Por eso se le dedicada el primer mes del ciclo del nuevo año, (enero que proviene de januarius) y se le relaciona con el principio (alfa) y con el fin (omega) de todas las cosas. Es el eje de la rueda del tiempo y se le conoce como el “Señor de la Eternidad”. También es el "Principium Deorum" o dios del principio y se le invocaba cada mañana al comienzo de la jornada de trabajo o cada vez que se iniciaba una nueva actividad.
¿QUIERE VIAJAR EN EL TIEMPO?CLARAMENTE HAY UN "AGUJERO DE GUSANO".
NO HAY PEOR CIEGO QUE EL QUE NO QUIERA VER.
|
 First Previous 2 to 2 of 2 Next  Last |
|
|
|
LA ISQUIERDA, INCLUSO ES ADICTA AL PASADO. ES UNA PATOLOGIA. VIVEN EN EL PASADO. LE TIENEN PANICO AL FUTURO, AUNQUE CON HIPOCRESIA. VIVEN NAVEGANDO EN INTERNET, TIENEN CELULARES, ETC,ETC Y LOS HIPOCRITAS SON ANTICAPITALISTAS.
OBVIAMENTE TODA UNA ENGAÑA PICHANGA PARA EL EGO
21. Apocalipsis 1:19 ESCRIBE las cosas que has visto, y las que son, y las que han de ser después de estas.
|
|
|
|
|
|
|
|
|
 |
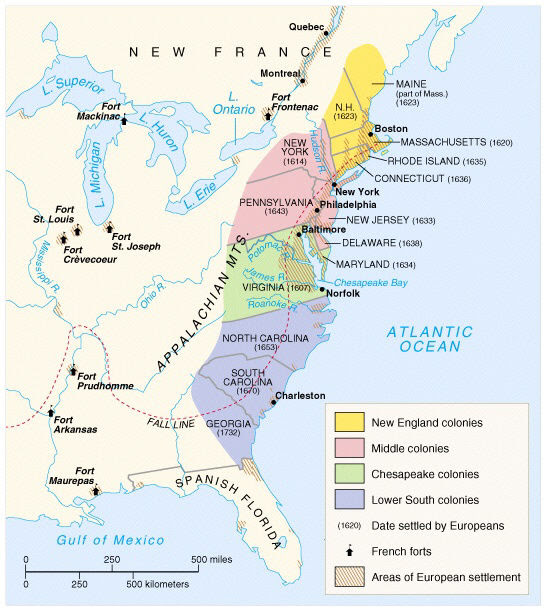| Aunque la leyenda del mapa está en inglés muestra con claridad los territorios colonizados por Inglaterra durante el siglo XVII. El primero de ellos había sido Virginia, descubierta por Walter Raleigh(hacia 1552-1618) en 1584 y donde se fundó el primer asentamiento inglés en los futuros Estados Unidos, la ciudad de Jamestown en 1607. Su nombre de Virginia se lo puso Raleigh en honor de la reina Isabel I de Inglaterra(1533-1603) que era conocida como "la reina virgen" ya que nunca se casó. En amarillo tenemos las colonias que formarían la Confederación de Nueva Inglaterra, donde se desarrollará la vida del capitán William Kidd, uno de los protagonistas de nuestro relato (imagen procedente dehttp://historiadoreshistericos.wordpress.com ) |
|
|
|
|
|
|
| Aunque la leyenda del mapa está en inglés muestra con claridad los territorios colonizados por Inglaterra durante el siglo XVII. El primero de ellos había sido Virginia, descubierta por Walter Raleigh(hacia 1552-1618) en 1584 y donde se fundó el primer asentamiento inglés en los futuros Estados Unidos, la ciudad de Jamestown en 1607. Su nombre de Virginia se lo puso Raleigh en honor de la reina Isabel I de Inglaterra(1533-1603) que era conocida como "la reina virgen" ya que nunca se casó. En amarillo tenemos las colonias que formarían la Confederación de Nueva Inglaterra, donde se desarrollará la vida del capitán William Kidd, uno de los protagonistas de nuestro relato (imagen procedente dehttp://historiadoreshistericos.wordpress.com ) |
|
|
|
|
|
|
|
|
|
|
|
| Así mismo Leonardo Da Vinci se rodeo de intelectuales de la época entre estos se encuentra el que es considerado EL MEJOR MATEMÁTICO EN SU ÉPOCA, fue un religioso católico.
Luca Pacioli
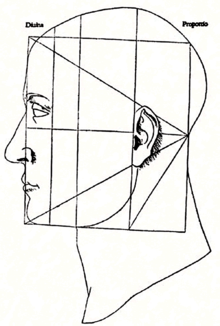
Representación de la cabeza humana acorde con La Divina Proporción (grabado de la edición de 1509, Paganino dei Paganini, Venecia).
Luca Pacioli, de nombre completo Fray Luca Bartolomeo de Pacioli o Luca di Borgo San Sepolcro, cuyo apellido también aparece escrito como Paccioli y Paciolo (Sansepolcro, 1445 - 1517), fue un fraile franciscano y matemático italiano, precursor del cálculo de probabilidades.
Analizó sistemáticamente el método contable de la partida doble usado por los comerciantes venecianos en su obra Summa de arithmetica, geometria, proportioni et proportionalita (Venecia, 1494), que a pesar de su título latino, incluye la primera obra matemática impresa en lengua romance. Es destacable que en la solución de uno de los problemas, utilizara una aproximación logarítmica, un siglo antes que John Napier.1
Su obra más divulgada e influyente es De Divina Proportione (De la Divina Proporción) término relativo a la razón o proporción ligada al denominado número áureo, escrita en Milán entre 1496 y 1498, y que trata también, en su primera parte, de lospolígonos y la perspectiva usada por los pintores del Quattrocento (Compendio Divina Proportione); en su segunda, de las ideas arquitectónicas de Vitruvio (Summa de arithmetica, geometria, proportioni et proportionalita); y en su tercera, de lossólidos platónicos o regulares (De quinque corporibus regularibus). Para ilustrarlo encargó dibujos a Leonardo da Vinci, que en la época formaba parte de la corte milanesa de Ludovico Sforza (il Moro).2
Entre 1477 y 1480 enseñó en la Universidad de Perugia, escribiendo a tal efecto el Tractatus mathematicus ad discipulos perusinos.3 Entre otras obras, escribió también De viribus quantitatis, sobre matemáticas y magia (1496–1508),4 una traducción de los Elementos de Euclides (Geometria, Venecia, 1509) y un manual de ajedrez (De ludo scacchorum).5 6
Sus influencias culturales
Pacioli oscila entre dos concepciones antitéticas de la matemática: una de índole pragmática y otra de índole especulativa e incluso mística; en relación a la segunda no duda en adherirla a las sugestiones místico-mágicas del platonismohumanista originado en la Academia de Marsilio Ficino.
Su obra debe ser entendida acorde con el contexto de la época del Renacimiento italiano. No es un matemático en el sentido epistemológico moderno (como su coetáneo Girolamo Cardano o, más tarde, Johannes Kepler). Pacioli, rememorando aPitágoras, declara que "la ciencia matemática se debe entender como la suma de aritmética, geometría, astrología (entonces confundida aún con la astronomía), música, perspectiva, arquitectura y cosmografía" (esta última en tiempos de Pacioli, aún indiferenciada de la cosmología, topografía y la geografía).La contabilidad moderna
Dentro del "Tractus XI- Particularis de computis et scripturis", nos dejó su legado a través de 36 capítulos (tratado de cuentas de contabilidad usando la partida doble) dando inicio, con eso a la contabilidad moderna.
- Aconseja utilizar cuatro libros: Inventario y Balances, Borrador o Comprobante, Diario y Mayor.
- Define reglas del principio matemático de la partida doble ( o por lo menos su parte fundamental):
1. No hay deudor sin acreedor.
2. La suma que se adeuda a una o varias cuentas ha de ser igual a lo que se abona.
3. Todo el que recibe debe a la persona que da o entrega.
4. Todo valor que ingresa es deudor y todo valor que sale es acreedor.
5. Toda pérdida es deudora y toda ganancia acreedora.
La Suma fue la primera publicación de aritmética y si bien fue él quien lo publicó es posible
que otros estudiosos también hayan hecho aportes a la misma.
http://es.wikipedia.org/wiki/Luca_Pacioli
|
|
|
|
|
|
NUMERO DE PLATA
SECRETO MASONICO DE LAS OCHO PUNTAS DE LA PLAZA DE SAN PEDRO
VATI-CAN= MEXI-CAN= AMRI-CAN= TEOTIHUA-CAN= CAN-A =TIERRA DE CANA-AN
SECRETO DE LA CANANEA DE MATEO 15 EN EL MARCO A MAGDALA
|
|
|
Primer
Anterior
2 a 14 de 74
Siguiente
Último
|
|
| |
|
|
©2024 - Gabitos - Todos los derechos reservados | |
|
|
Tema anterior
![La plaza del Vaticano [gay+estéril] fue diseñada con un reloj solar con octágono](http://www.geschichteinchronologie.com/welt/arch-Scott-Onstott-ESP/ph01-protocolo/026-028-Roma-numeros-13-28-364+1-d/017-plaza-Vaticano-gay-octagono-reloj-solar01.jpg "La plaza del Vaticano [gay+estéril] fue diseñada con un reloj solar con octágono")
