|
|
General: TEORIA DE CONJUNTOS- INTERSECCION=VESICA PISCIS
Elegir otro panel de mensajes |
|
|
Teoría de conjuntos
De Wikipedia, la enciclopedia libre

Hipótesis del continuo. La colección de todos los conjuntos de números naturales P( N) tiene la llamada potencia del continuo: tantos elementos como (por ejemplo) puntos en una recta. Su estudio es uno de los principales problemas en la teoría de conjuntos.
La teoría de conjuntos es una rama de las matemáticas que estudia las propiedades de los conjuntos: colecciones abstractas de objetos, consideradas como objetos en sí mismas. Los conjuntos y sus operaciones más elementales son una herramienta básica en la formulación de cualquier teoría matemática.[1]
Sin embargo, la teoría de los conjuntos es lo suficientemente rica como para construir el resto de objetos y estructuras de interés en matemáticas: números, funciones, figuras geométricas, ...; y junto con la lógica permite estudiar los fundamentos de esta. En la actualidad se acepta que el conjunto de axiomas de la teoría de Zermelo-Fraenkel es suficiente para desarrollar toda la matemática.
Además, la propia teoría de conjuntos es objeto de estudio per se, no sólo como herramienta auxiliar, en particular las propiedades y relaciones de los conjuntos infinitos. En esta disciplina es habitual que se presenten casos de propiedades indemostrables o contradictorias, como la hipótesis del continuo o la existencia de un cardinal inaccesible. Por esta razón, sus razonamientos y técnicas se apoyan en gran medida en la lógica matemática.
El desarrollo histórico de la teoría de conjuntos se atribuye a Georg Cantor, que comenzó a investigar cuestiones conjuntistas «puras» del infinito en la segunda mitad del siglo XIX, precedido por algunas ideas de Bernhard Bolzano e influenciado por Richard Dedekind. El descubrimiento de las paradojas de la teoría cantoriana, de conjuntos, formalizada por Gottlob Frege, propició los trabajos de Bertrand Russell, Ernst Zermelo, Abraham Fraenkel y otros a principios del siglo XX.
Teoría básica de conjuntos[editar]
La teoría de conjuntos más elemental es una de las herramientas básicas del lenguaje matemático. Dados unos elementos, unos objetos matemáticos como números o polígonos por ejemplo, puede imaginarse una colección determinada de estos objetos, un conjunto. Cada uno de estos elementos pertenecen al conjunto, y esta noción de pertenencia es la relación relativa a conjuntos más básica. Los propios conjuntos pueden imaginarse a su vez como elementos de otros conjuntos. La pertenencia de un elemento a a un conjunto A se indica como a ∈ A.
Una relación entre conjuntos derivada de la relación de pertenencia es la relación de inclusión. Una subcolección de elementos B de un conjunto dado A es un subconjunto de A, y se indica como B ⊆ A.
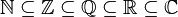
- El espacio tridimensional E3 es un conjunto de objetos elementales denominados puntos p, p ∈ E3. Las rectas r y planos α son conjuntos de puntos a su vez, y en particular son subconjuntos de E3, r ⊆ E3 y α ⊆ E3.
Álgebra de conjuntos[editar]
Existen unas operaciones básicas que permiten manipular los conjuntos y sus elementos, similares a las operaciones aritméticas, constituyendo el álgebra de conjuntos:
- Unión. La unión de dos conjuntos A y B es el conjunto A ∪ B que contiene cada elemento que está por lo menos en uno de ellos.
- Intersección. La intersección de dos conjuntos A y B es el conjunto A ∩ B que contiene todos los elementos comunes de A y B.
- Diferencia. La diferencia entre dos conjuntos A y B es el conjunto A B que contiene todos los elementos de A que no pertenecen a B.
- Complemento. El complemento de un conjunto A es el conjunto A∁ que contiene todos los elementos (respecto de algún conjunto referencial) que no pertenecen a A.
- Diferencia simétrica La diferencia simétrica de dos conjuntos A y B es el conjunto A Δ B con todos los elementos que pertenecen, o bien a A, o bien a B, pero no a ambos a la vez.
- Producto cartesiano. El producto cartesiano de dos conjuntos A y B es el conjunto A × B que contiene todos los pares ordenados (a, b) cuyo primer elemento a pertenece a A y su segundo elemento b pertenece a B.
Teoría axiomática de conjuntos[editar]
La teoría informal de conjuntos apela a la intuición para determinar cómo se comportan los conjuntos. Sin embargo, es sencillo plantear cuestiones acerca de las propiedades de estos que llevan a contradicción si se razona de esta manera, como la famosa paradoja de Russell. Históricamente ésta fue una de las razones para el desarrollo de las teorías axiomáticas de conjuntos, siendo otra el interés en determinar exactamente qué enunciados acerca de los conjuntos necesitan que se asuma el polémico axioma de elección para ser demostrados.
Las teorías axiomáticas de conjuntos son colecciones precisas de axiomas escogidos para poder derivar todas las propiedades de los conjuntos con el suficiente rigor matemático. Algunos ejemplos conocidos son:
Véase también[editar]
http://es.wikipedia.org/wiki/Teor%C3%ADa_de_conjuntos
|
|
|
|
|
|
AQUI ESTA LA CLAVE PARA TRATAR DE RACIONALIZAR LA "MAQUINA DEL TIEMPO"
LA INTERSECCION ES EL "AGUJERO DE GUSANO", OSEA EL VESICA PISCIS.
|
|
|
|
|
UNA FORMA SENCILLA DE RACIONALIZARLO, ES CON LA TEORIA DE CONJUNTOS, EN EL CONTEXTO A LA INTERSECCION, OSEA EL AGUJERO DE GUSANO. ES EN ESTE MARCO QUE EL SANTO GRIAL ES EL AGUJERO DE GUSANO A NIVEL MUNDIAL, PORQUE INSISTO, TODO ESTA CODIFICADO. EL SANTO GRIAL ES LO QUE UNE, POR EJEMPLO, TODAS LAS CULTURAS A NIVEL MUNDIAL, LA MITOLOGIA, LA CIENCIA, LA ARQUITECTURA, LA QUIMICA, LA ALQUIMIA, LA FISICA, ETC,ETC.
EL GRIAL ES EL AGUJERO DE GUSANO = MAQUINA DEL TIEMPO = EXPERIMENTO FILADELFIA
|
|
|
|
|
|
|
Intersección de conjuntos
De Wikipedia, la enciclopedia libre
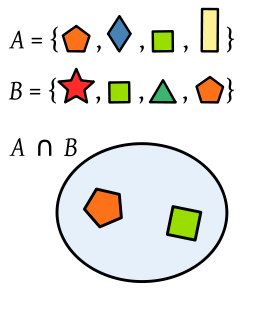
La intersección de A y B es otro conjunto A ∩ B que contiene sólo los elementos que pertenecen tanto a A como a B.
En teoría de conjuntos, la intersección de dos (o más) conjuntos es una operación que resulta en otro conjunto que contiene los elementos comunes a los conjuntos de partida. Por ejemplo, dado el conjunto de los números pares P y el conjunto de los cuadrados C de números naturales, su intersección es el conjunto de los cuadrados pares D :
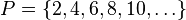  
La intersección de conjuntos se denota por el símbolo ∩ por lo que D = P ∩ C.
Dados dos conjuntos A y B, su intersección es otro conjunto que contiene los elementos que pertenecen a ambos conjuntos:
La intersección de dos conjuntos A y B es otro conjunto A ∩ B cuyos elementos son los elementos comunes a A y B :

|
Ejemplo.
- Sean A = {5, λ, ♠, c} y B = {ω, c, 0, Δ, 5, R}. Entonces la intersección es A ∩ B = {5, c}.
- Sean los conjuntos de números naturales C = {n: n es una potencia de 2} y D = {n: n es un cubo}. Su intersección es C ∩ D = {n: n es una potencia de 2 y un cubo} = {n: n es una potencia de 2 cuyo exponente es múltiplo de 3} = {8, 64, 512, ...}.
- Sean los conjuntos de números pares e impares. Su intersección es el conjunto vacío ∅, ya que no existe ningún número natural que sea par e impar a la vez.
Cuando la intersección de dos conjuntos es vacía, se dice que son disjuntos:
Dos conjuntos A y B se dicen disjuntos si su intersección es el conjunto vacío:
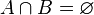
|
Generalizaciones[editar]
La intersección de un número finito de conjuntos, superior a dos, se define teniendo en cuenta que, debido a la propiedad asociativa (más abajo), el orden en el que se intersequen los conjuntos es irrelevante:
La definición más general en teoría de conjuntos se refiere a una familia de conjuntos, un conjunto cuyos elementos son conjuntos a su vez:
Sea M una familia de conjuntos. Su intersección ∩M se define como:

|
De este modo, la intersección de un número finito de conjuntos es sólo un caso particular de esta definición general:
- A ∩ B = ∩M, donde M = {A, B}
- A1 ∩ ... ∩ An = ∩M, donde M = {A1, ..., An}
La intersección general de conjuntos se denota de diversas maneras:

donde esta última se aplica en el caso de que utilicemos un conjunto índice, definiendo M como {Ai: i ∈ I}.
Propiedades[editar]
De la definición de intersección puede deducirse directamente:
- Idempotencia. La intersección de un conjunto A consigo mismo es el propio A :

- La intersección de A y B es un subconjunto de ambos:

- La intersección de un conjunto B con un conjunto A que lo contenga, deja a B inalterado:
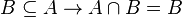
|
La intersección de conjuntos posee también propiedades similares a las operaciones con números:
- Propiedad asociativa. La intersección de los conjuntos A y B ∩ C es igual a la intersección de los conjuntos A ∩ B y C :

- Propiedad conmutativa. La intersección de los conjuntos A y B es igual a la intersección de los conjuntos B y A :
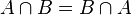

|
Todas estas propiedades se deducen de propiedades análogas para la conjunción lógica.
En relación con la operación de unión existen unas leyes distributivas:
Propiedad distributiva
- A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C), y por tanto:
- A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C), y por tanto:
|
Teoría axiomática[editar]
En las teorías axiomáticas de conjuntos usuales, como ZFC o NBG, la existencia de la intersección de una familia de conjuntos no se postula de manera independiente, sino que se demuestra como consecuencia del esquema axiomático de reemplazo.
Referencias[editar]
- Dorronsoro, José; Hernández, Eugenio (1996). Números, grupos y anillos. Addison-Wesley/Universidad Autónoma de Madrid. ISBN 84-7829-009-5.
- Lipschutz, Seymour (1991). Teoría de conjuntos y temas afines. McGraw-Hill. ISBN 968-422-926-7.
Véase también[editar]
|
|
|
|
|

geometria-analitica-y-...
La intersección entre dos
1411 × 778 - 83k - jpg |
e-ducativa.catedu.es
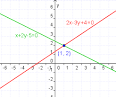
Intersección de rectas
300 × 250 - 12k - png |
profesordedibujo.com
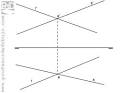
Intersección entre dos rectas.
400 × 300 - 30k - jpg |
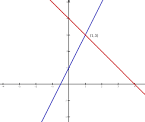
misdeberes.es
Archivo para la respuesta
853 × 720 - 59k - jpg |
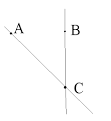
html.rincondelvago.com
Radiotelemetría
327 × 356 - 4k - png |

tec-digital.itcr.ac.cr
Rectas perpendiculares
343 × 402 - 13k - jpg |
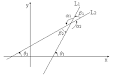
zeidyquiroz.blogspot.com
Si la recta L1, con ecuación y
322 × 204 - 3k - gif |
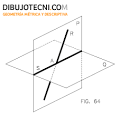
dibujotecni.com
Intersección recta-plano
345 × 337 - 9k - png |
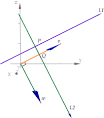
tec-digital.itcr.ac.cr
Rectas perpendiculares
287 × 325 - 5k - gif |

celiagarciacgl.blogspo...
Es
151 × 112 - 6k - png |

krithowhond3r.blogspot...
de interseccion entre dos
1203 × 1237 - 99k - png |
herramientasingenieria...
de las dos rectas será el
486 × 324 - 16k - gif |
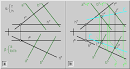
geometriadescriptiva.com
Intersección (i), entre un
489 × 260 - 7k - gif |

wiki-postulado.wikispa...
Siguiente
520 × 325 - 9k - png |
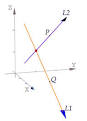
tec-digital.itcr.ac.cr
Intersección de rectas
256 × 357 - 9k - jpg |

html.rincondelvago.com
RECTA PERPENDICULAR A UN PLANO
531 × 342 - 3k - png |

youtube.com
maxresdefault.jpg
1280 × 654 - 52k - jpg |

geometria-analitica-y-...
puntos de intersección.
1600 × 1212 - 177k - jpg |
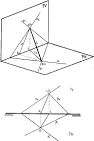
eodos.net
Intersección de planos
491 × 738 - 7k - png |

winmates.net
entre dos rectas.
176 × 68 - 2k - png |
|
|
|
|
|
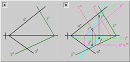
geometriadescriptiva.com
Intersección (i), entre dos
489 × 233 - 6k - gif |

geometriadescriptiva.com
Intersección (i), entre un
489 × 260 - 7k - gif |

webdelprofesor.ula.ve
Intersección entre dos Planos
494 × 698 - 18k - gif |
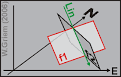
geovirtual2.cl
Figura 1: Dos planos se
360 × 229 - 5k - gif |
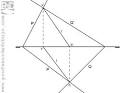
profesordedibujo.com
Intersección entre dos planos
400 × 300 - 36k - jpg |

html.rincondelvago.com
Elijamos como plano auxiliar
491 × 738 - 7k - png |
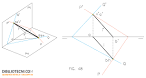
dibujotecni.com
Intersección de dos planos
882 × 473 - 21k - png |

datateca.unad.edu.co
real entre los dos planos,
593 × 365 - 29k - jpg |

elotrolado.net
Determinad la intersección
1275 × 1754 - 88k - jpg |
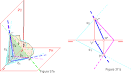
dibujotecnico.ramondel...
INTERSECCIÓN DE DOS PLANOS
521 × 291 - 9k - gif |
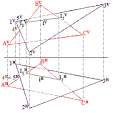
ucla.edu.ve
Intersección entre Planos
270 × 270 - 5k - gif |
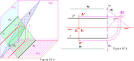
dibujotecnico.ramondel...
INTERSECCIÓN DE DOS PLANOS
580 × 265 - 10k - gif |

sistema-diedrico.blogs...
intersección de los dos
320 × 159 - 46k - jpg |
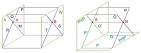
lanubeartistica.es
El elemento común a dos planos
736 × 279 - 37k - jpg |

dibujotecni.com
Intersección recta-plano
345 × 337 - 9k - png |
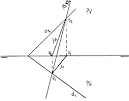
html.rincondelvago.com
INTERSECCION DE LOS PLANOS 1-
472 × 370 - 3k - png |
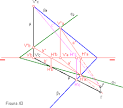
dibujotecnico.ramondel...
Hallaremos la intersección de
388 × 340 - 5k - gif |
unalmed.edu.co
Intersecciones de planos: Sí,
133 × 129 - 7k - jpg |
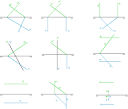
lanubeartistica.es
planos que se cortan, dos
464 × 396 - 13k - png |

aulafacil.com
Posición Relativa de dos
349 × 113 - 8k - jpg |
|
|
|
|
|
CRUZ DE CRISTO = INTERSECCION = VESICA PISCIS = ALQUIMIA DE LA ALQUIMIA = AGUJERO DE GUSANO = SANTO GRIAL
|
|
|
|
|
CRUZ DE CRISTO = INTERSECCION = VESICA PISCIS = ALQUIMIA DE LA ALQUIMIA = AGUJERO DE GUSANO = SANTO GRIAL
|
|
|
|
|
|
DAVINCI/DAVID
A/ESPADA/BLADE/SIMBOLO FALICO
V/CALIZ/CHALICE/RECIPIENTE/SIMBOLO FEMENINO
ESTRELLA DE DAVID ES LA ALQUIMIA, OSEA LA UNION ENTRE EL HOMBRE Y LA MUJER

mediateca.educa.madrid...
6 puntas
301 × 350 - 19k - php |

primariaalcompas.blogs...
Colorear una estrella de 6
500 × 500 - 21k - bmp |

imagui.com
Geometría | Black Dog
666 × 645 - 48k - jpg |

portaldesalta.gov.ar
Convertida en Estrella de 6
136 × 145 - 6k - jpg |
EL HEXAGONO ES EL AGUJERO DE GUSANO. INSISTO, ES LA INTERSECCION ENTRE LOS DOS TRIANGULOS EQUILATEROS QUE FORMAN LA ESTRELLA DE 6 PUNTAS. DICHA INTERSECCION=VESICA PISCIS= SANTO GRIAL.
|
Siguiendo estudiando el 17 del septimo mes (Genesis 8:4) es curioso que desde el 1 de enero hasta el 17/7 tenemos 198 dias (la misma cantidad de dias que hay desde el 1 de Nissan hasta el 21 de Tisri). Otro dato contextual es que en el 17/9/1787 (17 de septiembre o septimo mes) dia que se impuso la CONSTITUCION DE LOS EEUU, en el contexto a LUNA NUEVA EN LUNA LLENA CAYO TAMBIEN EL 21 DE TISRI, OSEA OSHANAH RABBAH.
RABA/AMMAN/FILADELFIA/7 COLINAS
The Franciscan church is attached to the Church of the Holy Sepulchre by the Magdalene chapelOne of the most holiest churches, located in Jerusalem at the traditional site of Golgotha - the place of Jesus Crucifixion and burial. Matthew 27: 33, 60: "And when they were come unto a place called Golgotha....And laid it in his own new tomb, which he had hewn out in the rock: and he rolled a great stone to the door of the sepulchre, and departed"http://www.biblewalks.com/Sites/Sepulcher.html#MagdaleneOn the floor, in front of the Holy Sepulchre, is a mosaic figure of a double headed eagle - symbol of the Byzantine empire and the Greek Orthodox church.that is also the symbol used by  Morals and Dogma by Pike and the Scottish Rites The first mention of a double-headed eagle in the West dates from 1250, in a roll of arms of Matthew of Paris for Emperor Frederick II of the Holy Roman Empire. Usually depicted black on a gold background, it replaced the earlier single-headed eagle, and was subsequently adopted in the coats of arms of many German cities and aristocratic families. After the dissolution of the Holy Roman Empire in 1806, the double-headed eagle was retained by the Austrian Empire, and served also as the coat of arms of the German Confederation. The double-headed eagle was part of the emblem of the Order of the Solar Temple. This cult was started by Joseph Di Mambro and Luc Jouret in 1984 in Geneva. It gained notoriety in 1994 when members of the cult committed mass suicide and murders in two villages in Switzerland, followed in 1997 by suicide/murders in Canada. http://en.wikipedia.org/wiki/Double-headed_eagleThe Greek Orthodox chapel has a circle floor with a sun and wavy rays coming from itthere is a rock there which the crack goes down to the chapel of Adam belowit is said that Jesus blood dripped down to reach the skull of AdamMagdalen's star has points and a green stone center http://www.sacred-destinations.com/israel/jerusalem-holy-sepulchre-photos/slides/franciscan-mass-cc-irithThe Franciscans he impact of the Franciscan Third Order Secular upon the feudal society of medieval Europe has been held to be considerable. Among its ways of impacting that era was the prohibition on the brothers of the Order from bearing arms. This stance of pacifism in a society with frequent feuds and wars was upheld by the authority of the Church, and limited the ability of the nobility and towns to demand that all men be subject to serving in battle. Also, the admission to the Order of members from all stations in life on an equal basis was a mechanism for promoting social change in a period of rigid social stratification. The Third Order has known many notables among its members. Outstanding among them is Saint Elisabeth of Hungary, though it is not established to all that she ever formally joined;[3] she is, however, Patroness of the Order. Additionally, she is traditionally paired with St. Louis, King of France, declared Patron of the Order. Among other notable figures were: St. Ferdinand, King of Castile; St. Elizabeth of Portugal, grand-niece of the first St. Elizabeth; St. Rosa of Viterbo; St. Margaret of Cortona; St. Thomas More; Blessed Umiliana Cerchi; Blessed Angela of Foligno; St. Ivo of Kermartin; Saint John Vianney, the famed Curé of Ars, France. Of names celebrated in history for literature, arts, politics, inventions, etc., Blessed Raymond Lull; Dante, Giotto, Petrarch, Cola di Rienzo, Christopher Columbus, Vasco da Gama, Cervantes, Lope de Vega, Galvani, Alessandro Volta, Garcia Moreno, Franz Liszt, and Lady Georgiana Fullerton. Popes Pius IX and Leo XIII were members of the Third Order, as also were Pope St. Pius X and the Blessed Pope John XXIII The Third Order of Saint Francis Canada The Third Order of St. Francis was established by the Friars Minor Recollects at Quebec in 1671, and some years later at Three Rivers and Montreal. Considering the sparse population of the country, it was in a flourishing condition. In 1681 a Recollect notes that "many pious people of Quebec belong to the Third Order". After the cession of Canada to England, the Third Order, deprived of its directors, the Recollect Franciscan friars, seemed to have disappeared gradually, only to flourish anew thirty years after the death at Montreal in 1813 of the last Recollect friar. The Third Order was re-established about 1840 by Mgr. Ignatius Bourget, Bishop of Montreal. Fervent fellow-labourers helped the holy prelate to spread the Third Order in Montreal, notably Canon J.A. Paré and the Sulpicians C. E. Gilbert and A. Giband. Mgr. Bourget established a fraternity of women, 6 May 1863, and one of men, 13 June 1866; both were directed by the Sulpicians till 1874, by Canon P. E. Dufresne from 1874 till 1881, by the Jesuits from 1881 till 1888, and by the Sulpicians from 1888 till 1890; since then by the Friars Minor. Mgr. Fabre, successor to Bishop Bourget, in a letter (3 September 1882) to the priests and faithful of his diocese, says: "We have in our midst the tertiaries of St. Francis, who are known to you all by the edification they give, and by the good odour of all the virtues which they practise in the world." The Third Order was reintroduced at Quebec almost at the same time as at Montreal. On 19 November 1859, Father Flavian Durocher, O.M.I., received the profession of two women, after a year's novitiate. These were joined by others, until in 1876 Quebec City alone possessed over 200 tertiaries, while in the Province of Quebec several parishes had groups of tertiaries. Saint Francis of Assisi rejected the urban materialism of his parents and local church. He established a mendicant, or beggar, lifestyle for the followers of his church-approved order—Franciscan friars for men and the Poor Clares for women. Many religious thinkers in the 1200s were influenced by the earlier philosophy of Christian Neoplatonism, a synthesis of Plato’s ideals and Christian mysticism. Under that influence, they rejected the Aristotelian focus on rationalizing religion and believed God's divine revelation could best be understood through experience. The Cistercian Bernard of Clairvaux, who died in 1153, feared that Abelard's scholastic logic would deaden true spiritual understanding. Later, Bonaventure, a Franciscan who lived from 1221 to 1274, developed a mystical philosophy guiding Christians toward contemplation of the ideal realm of God. http://history-world.org/dynamic_culture_of_medieval_euro.htmAlexander of Hales, Bonaventure, and John Duns Scotus, the "Doctor of Wonders" Roger Bacon, and the well-known mystic authors and popular preachers David of Augsburg and Berthold of Regensburg. as well as Anthony of Padua
|
|
|
|
|
|
|
|
Fermentation - nigredo - bread and wine of Christ    La vesica piscis (vejiga de pez en latín) es un símbolo hecho con dos círculos del mismo radio que se intersecan de manera que el centro de cada círculo está en la circunferencia del otro. Esta forma se denomina también mandorla (que significa "almendra" en italiano).
Se produce el mismo patron. LA SERPIENTE SE MUERDE LA COLA.
EL RELOJ DE ARENA TAMBIEN TIENE UN AGUJERO DE GUSANO Y CUMPLE EL MISMO PATRON.EL ORIGEN DEL PORQUE EXISTEN DOS PERIODOS DE 12 HORAS EN EL DIA, TAMBIEN TIENE ESTE NEXO E INCLUSO TAMBIEN CON EL ZEP TEPI DE LA PRECESION DE LOS EQUINOCCIOS.
|
JESUCRISTO FUE CRUCIFICADO EL 15 DE MARZO (15/3= VESICA PISCIS), OSEA EL 14 DE NISSAN O PRIMER MES HEBREO DEL AÑO 33 D.C. ESTO EXPLICA TAMBIEN EL NEXO DE LA CRUZ DEL SEÑOR CON VESICA PISCIS. EL ASESINATO DE JULIO CESAR, TAMBIEN FUE UN 15/3.
|
|
|
|
|

taringa.net
Cubo mágico: el número de Dios
480 × 500 - 52k - jpg |
taringa.net
cubo
500 × 500 - 24k - jpg |

vivienlos80s.com
cubo-rubik cubo-magico
390 × 400 - 28k - jpg |

taringa.net
armar
400 × 400 - 28k - jpg |

taringa.net
Cubo Rubik
1600 × 1600 - 1740k - png |

articulo.mercadolibre....
Cubo Magico Como El Rubik
500 × 500 - 21k - jpg |

tiempoconsciente.com
4_10521_rubik20generation.jpg
1181 × 948 - 127k - jpg |

articulo.mercadolibre....
Cubo Mágico 5x5 - Ideal
292 × 280 - 20k - jpg |

articulo.mercadolibre....
Loading zoom.
1200 × 900 - 126k - jpg |

tiempoconsciente.com
récord con el cubo mágico
626 × 572 - 66k - jpg |

mipunto-devista.blogsp...
muchos "Cubos de Rubik",
400 × 267 - 247k - png |

teinteresasaber.com
fue el creador del Cubo,
327 × 246 - 18k - jpg |

taringa.net
Cubo Rubik celebra 40 años de
800 × 600 - 34k - jpg |

bloganthonyucv.blogspo...
Solucion del Cubo Magico XD
500 × 369 - 28k - jpg |

taringa.net
Combinaciones
399 × 400 - 42k - jpg |

tendenciasmag.com
El cubo mágico, un militante
650 × 430 - 22k - jpg |

es.walyou.com
2 Alcancia cubo Rubik
521 × 423 - 24k - jpg |

es.wikipedia.org
El interior de un cubo de
232 × 199 - 28k - jpg |

solostocks.com
Cubo Mágico
500 × 500 - 29k - jpg |

pocoseso.com
del Rubik - Cubo Magico -
450 × 338 - 28k - jpg |
Búsquedas relacionadas con cubo magico
LA MONSTRUOSA CRUZ DE MALTA SALE DEL OCTOGONO, EN FUNCION A LA DIVISION EN TRES DE CADA LADO. EN ESTE MARCO SI LO MULTIPLICAMOS POR EL NUMERO 3, TENEMOS EL MONSTUOSO NUMERO 9, QUE TIENE REFERENCIA A LOS 9 MESES LUNARES DE GESTACION DE UN BEBE. INCLUSO MULTIPLICADOS POR EL NUMERO 4 TAMBIEN TENEMOS LOS 36 SABADOS LUNARES DE GESTACION DE UN BEBE. TODO EN EL CONTEXTO AL NUMERO 8, QUE ES EL NUMERO DE LA RESURRECCION DEL SEÑOR.
RESURRECCION DE JESUCRISTO = NACIMIENTO DE UN BEBE
CREALO PORQUE NO LE QUEDA OTRA
 First First  Previous 2 to 2 of 2 Next Previous 2 to 2 of 2 Next  Last Last  |
|
|
|
EL CUBO MAGICO, SI OBSERVAMOS ESTA DISEÑADO EN UN PATRON CON REFERENCIA AL OCTOGONO. SI CONTAMOS TIENE 27 CUBITOS MAS EL CUBO MADRE, OSEA EL GRANDE, SON 28, OSEA UNA REFERENCIA A LOS 4 SABADOS LUNARES (4*7=28 DIAS). ES CLARA LA REFERENCIA AL CUARTO MANDAMIENTO CON REFERENCIA AL SEPTIMO DIA, EN EL CONTEXTO AL VERDADERO REPOSO QUE ES EN EL CONTEXTO A LAS FASES DE LA LUNA. TAMBIEN OBSERVAMOS QUE TIENE 7 CUBITOS CENTRALES FIJOS Y UNO QUE ES EL CENTRO DEL CENTRO QUE ES LA INTERSECCION O EL VESICA PISCIS DE ESTOS 7 ULTIMOS. INSISTO, EL CUBITO CENTRAL SIMBOLIZA AL GRIAL. TODO ESTO ES ALQUIMIA EN UN FUERTE CONTEXTO MATEMATICO. SABIDURIA / SOPHIA / SABADO / CODIGO DA VINCI.
|
|
|
|
|
|
|
LA MISMA CRUZ (EN SU MARCO CON LA INTERSECCION) TIENE RELACION CON EL "AGUJERO DE GUSANO". OSEA QUE EL NEXO DEL CAMINO DE SANTIAGO CON REFERENCIA A LA CRUZ DEL NORTE (CONSTELACION DEL CISNE) TIENE ESE MARCO.
|
|
|
|
|
LA INDEPENDENCIA DE ESTADOS UNIDOS CODIFICADA EN LAS 24 HORAS QUE TIENE UN DIA
EFECTIVAMENTE TENEMOS QUE EN 74 DIAS (INDEPENDENCIA DE EEUU FUE UN 4/7 O 7/4) TENEMOS EXACTAMENTE 1776 HORAS (AÑO 1776)
 |
|
24 * 74 = 1776
|
LAS MATEMATICAS SON EXACTAS PARA EL TODOPODEROSO
HECHOS 12:12 (12+12=24 HORAS)
JUAN MARCOS= SANTO GRIAL
EL DIA NUMERO 74 DEL CALENDARIO LUNI-SOLAR HEBREO ES EL 15 DE SIVAN O 15/3 (VESICA PISCIS="OJO DE GATO")
ULTRA SECRETO DEL PORQUE GEORGE MC FLY MUERE EN UN 15/3 EN LA PELICULA "VOLVER AL FUTURO II". ES OBVIA LA REFERENCIA AL "EXPERIMENTO FILADELFIA", EN EL MARCO A LA CREACION DIVINA.
EN 36 DIAS TENEMOS
 |
|
24 * 36 = 864
|
OBVIO NEXO CON SIRIO / JERUSALEN
EN 33 DIAS
 |
|
24 * 33 = 792
|
OBVIO NEXO CON LOS 7920, QUE ES EL DIAMETRO DE LA TIERRA EN MILLAS INGLESAS, EN EL MARCO AL DISEÑO DE LA GRAN PIRAMIDE.
|
|
|
|
|
Sabemos que Vesica Piscis esta en funcion al a los 153 peces de Juan 21:11.
 Aqui tenemos a Pi - la circunferencia del toro y la vesica piscis 256/153 equivalente a la raiz cuadrada de 3 En el hipercubo las coordinadas binarias de Piscis son decimal 3 y binario 11 153 los pescados de Jesus en la biblia
Sapientia Aedificavit Sibi Domum. Es decir, "la sabiduría ha edificado aquí su casa". Resulta curioso que la misma frase aparece en el Evangelio de María Magdalena, un texto apócrifo. Se dice que en el interior de esta iglesia y de otras muchas de Venecia está escondido el tesoro de los templarios. Pero no hay ninguna prueba de ello. Para terminar ya con esta entrada me gustaría que nos acercásemos un momento a uno de los edificios más emblemáticos de Venecia: el Palacio Ducal.
|
|
|
|
|

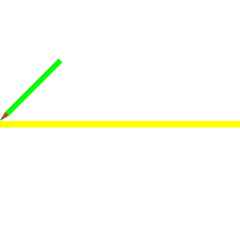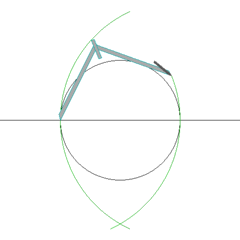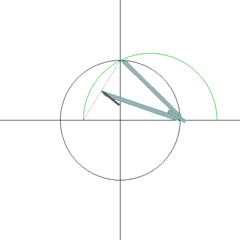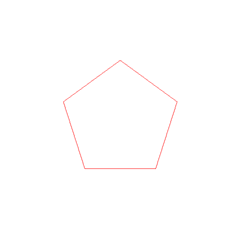
Sabemos que Vesica Piscis esta en funcion al a los 153 peces de Juan 21:11.
 Aqui tenemos a Pi - la circunferencia del toro y la vesica piscis 256/153 equivalente a la raiz cuadrada de 3 En el hipercubo las coordinadas binarias de Piscis son decimal 3 y binario 11 153 los pescados de Jesus en la biblia   
I have a lot to say about pythagorean triangles in my videos. In particular I have found many references to 5:12:13 triangles and 5:12 rectangles (that’s 2 of the triangles put together) in Stonehenge and the whole region surrounding it, in Washington DC, Paris, and Jerusalem. Someone who listened to my first Red Ice interview contacted me with a major discovery he made in regards to the 5:12 proportion. Brace yourself…

A rectangle measuring 5 feet by 12 feet has an area of 8640 square inches. This is something I can work with. I’m never going to be able to build an 864 foot solar Osiris talisman on a geodetic hot spot, but I think I can manage making a few raised garden beds measuring exactly 5 by 12 feet. And where I live in Canada (above 50 degrees North) can really use more resonance with the Sun.
If you saw SIPS Volume 1, you might recall that Stonehenge has its station stones which describe a 5×12 rectangle.

from SIPS Volume 1
Stonehenge is also 33.33° from Solomon’s Temple.

Sapientia Aedificavit Sibi Domum. Es decir, "la sabiduría ha edificado aquí su casa". Resulta curioso que la misma frase aparece en el Evangelio de María Magdalena, un texto apócrifo. Se dice que en el interior de esta iglesia y de otras muchas de Venecia está escondido el tesoro de los templarios. Pero no hay ninguna prueba de ello. Para terminar ya con esta entrada me gustaría que nos acercásemos un momento a uno de los edificios más emblemáticos de Venecia: el Palacio Ducal.
|
|
|
 Primer Primer
 Anterior
3 a 17 de 17
Siguiente Anterior
3 a 17 de 17
Siguiente
 Último
Último

|
|
| |
|
|
©2025 - Gabitos - Todos los derechos reservados | |
|
|


The blade and chalice guarding o'er her gates.
Adorned in masters' loving art, she lies.
She rests at last beneath the starry skys.