|
|
General: YHWH (RELACION CON EL NUMERO DE ORO PHI=1.618...)
Elegir otro panel de mensajes |
|
|
http://lucesquenobrillan.blogspot.com.ar/2014/01/la-probable-pronunciacion-del-nombre.html
La probable pronunciación del nombre que representa el tetragrámaton griego YHWH
Hoy día se conocen dos pronunciaciones del tetragrámaton o cuatro letras del hipotético nombre de Dios que en griego se escribe con las vocales YHWH (Ipsilon, Eta, Omega, Eta, son vocales, no consonantes), que en el alfabeto griego se pronuncian IEUE, respectivamente, o también IEOE, ya que la letra W (Omega, no uve doble) admite las dos pronunciaciones (U y O). Por lo general en las biblias de las iglesias protestantes el tetragramaton se transcribe como Jehovah. En las católicas, como Yahweh, forma ésta que, según los eruditos en la materia, sería la pronunciación más correcta del tetragramaton con que se representa el nombre divino. Otros eruditos defienden la forma Yahwah.
La pronunciación Jehovah se origina al haber intercalado la Iglesia Católica al tetragrámaton las vocales de la palabra Adonaí (Señor), supliendo la primera A por una E. Indistintamente se pronunciaba el nombre divino como Jehovah o Jehovih. La escritura y pronunciación Jehovah fue la más usada en las biblias católicas. Cuando los protestantes se separaron, adoptaron la forma Jehovah que aparece en sus biblias hasta este día. Posteriormente la Iglesia Católica, para diferenciar la pronunciación, adoptó la forma Yaweh que algunos estudiosos entendían como más correcta, pero que a día de hoy no se sabe si realmente lo es, y lo más probable es que no lo sea.
El historiador Diodoro de Sicilia, del siglo I antes de nuestra era, escribe que la pronunciación del tetragrámaton era IAO. La transcripción YHWH en griego habría conservado la pronunciación original hebrea. Según ello, una de dos, o las letras H no tendrían otra función que la de alargar el sonido vocal de las caracteres precedentes, a saber, Y, que se pronunciaría IAA, y W, con pronunciación de O alargada. La pronunciación sonaría, pues, como IAAOO; o bien ambas H eran mudas y el nombre sonaría como IAO ó YAHOH. No ha de olvidarse que el nombre divino abreviado aparece en la Biblia como YAH ó JAH.
Cada vez más eruditos están convencidos de que IAO ó YAHOH era la pronunciación correcta del tetragrámaton escrito YHWH en griego. Siglos atrás así lo habían creído estudiosos como Orígenes, Ireneo y Clemente de Alejandría, aunque este último defendía la expresión IAOU, dándole el sonido OU a la W. Tal pronunciación del hipotético nombre de Dios que esconde el tetragrámaton YHWH estaría de acuerdo con los arcaicos símbolos o caracteres representados como IO, donde la I se pronunciaba IA.
El símbolo I representaba en la antigüedad el concepto masculino, en tanto que O aludía al femenino. Ambos juntos forman IO, significando que la persona a quien se atribuyen los dos símbolos reúne en sí mismo los principios masculino y femenino, siendo el creador de cuanto existe, material o energéticamente. En griego los símbolos IO se funden en una sola letra, la que se denomina PHI, pronunciada F, que encaja el distintivo I en O. PHI es asimismo la designación del número áureo, de valor 1,618, empleado sobre todo en el arte arquitectónico maestro, algo que no está al alcance de todos los arquitectos. Por tanto PHI designa sapiencia profunda. No habría, pues, otra denominación más acorde para la sapiencia del Ser Creador que la representación IO, los principios masculino y femenino, ocultos en el tetragrámaton YHWH y pronunciado YAHOH ó IAO.
|
|
|
Primer
Anterior
2 a 13 de 13
Siguiente
Último
|
|
|
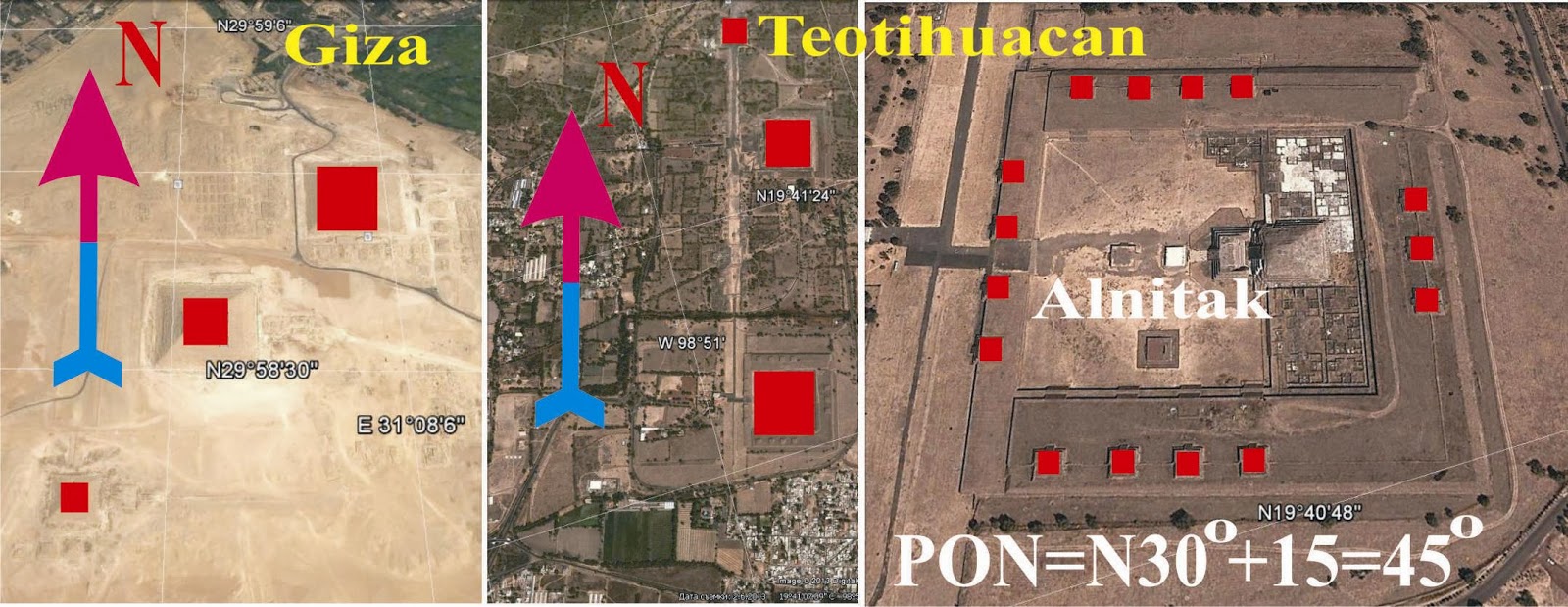
TEOTIHUACAN-GIZE-NUMERO DE ORO PHI=1.618-RELACION CON LA INDEPENDENCIA DEL ESTADO DE ISRAEL
ISRAEL
ISIS
RA
ELOHIM
330 AÑOS EXACTOS MAS 1618=1948 (INDEPENDENCIA DE ISRAEL)
¿Qué es phi?
Phi y la serie de Fibonacci
Funciones trigonométricas
Razones matemáticas
Pentágono
Espirales Áureas
Inicio :: Ver temas relacionados: Decalogo Geometria Sagrada :: Número de Oro :: Merkaba
¿Qué es phi?
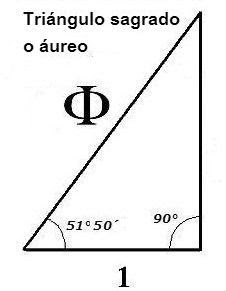
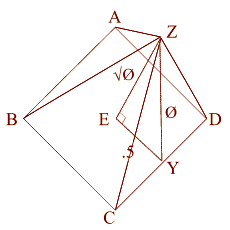
Phi (1.618033988749895... ), pronunciado como fi, es un numero irracional como Pi ( 3.14159265358979... ), pero con muchas características matemáticas inusuales. Phi es la base de la Proporción Dorada. La razón o proporción determinada por Phi (1.618...) era conocida por los Griegos como la “Sección Dorada” y por los artistas del renacimiento como la “Proporción Divina”. También se le conoce como la razón Dorada o la Proporción Áurea.
Phi, como Pi, es una razón definida por una construcción geométrica.
Pi es la relación de la circunferencia de un círculo respecto a su diámetro. Phi es la proporción de los segmentos de una línea que resultan cuando una línea es dividida de una forma única y especial.
La línea es dividida para que la proporción de la longitud de la línea entera (A) respecto a la longitud del segmento de la línea mayor (B) sea igual que la proporción de la longitud del segmento de la línea mayor (B) a la longitud del segmento de la línea menor (C)
Esto es que A es 1.618... veces B, y B es 1.618… veces C. Recíprocamente, C es 0.618... de B y B es 0.618... de A. Phi con mayúscula "Phi" es 1.6180339887..., mientras que phi con minúscula es 0.6180339887, el reciproco de Phi o Phi menos 1.
Lo que hace a phi incluso mas inusual es que puede derivarse de muchas formas y ser encontrado en proporcionalmente en el universo. Phi F puede ser derivado por: la serie numérica descubierta por Leonardo Fibonacci, matemáticas y geometría.
Phi y la serie de Fibonacci
Leonardo Fibonacci, por herencia del mundo árabe, descubrió la serie que nos lleva a phi. En el siglo XII, Leonardo Fibonacci descubrió una serie numérica simple que es la base de la increíble relación que encontramos detrás de phi. Empezando con 0 y 1, cada número de la serie es simplemente la suma de los dos anteriores. Así: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, . . .
La razón (proporción) de cada par sucesivo de números en la serie se aproxima a phi (1.618. . .). Así si dividimos 5 entre 3 es 1.666..., y 8 entre 5 es 1.60. En la medida en la que vamos mas lejos del 0 (punto de inicio de la secuencia) nos acercamos al valor de phi.
La tabla de abajo nos muestra como las proporciones de números sucesivos en la serie Fibonacci se aproxima a Phi.
Puedes computar cualquier número de la serie Fibonacci fácilmente. Usa phi para saber cualquier numero (n) de la serie Fibonacci (f)
fn = Fn / 5½
Phi puede derivarse matemáticamente resolviendo la ecuación:
n2 - n1 - n0 = 0 que es lo mismo que n2 - n - 1 = 0
Esta ecuación la rescribimos y nos queda así:
n2 = n + 1 y 1 / n = n - 1
La solución a la ecuación es la raíz cuadrada de 5 más 1 dividido entre 2
( 5½ + 1 ) / 2 = 1.6180339... = F
Esto resulta en dos propiedades únicas de phi:
Si elevas al cuadrado a phi, obtienes un numero exactamente 1 mayor que phi: 2.6180...
F2 = F + 1
Si divides a phi entre 1, obtienes un numero exactamente a 1 menos phi: 0.6180...:
1 / F = F - 1
Phi, curiosamente, puede ser expresado en cinco: 5 ^ .5 * .5 + .5 = F
Puedes usar phi para computar un número n en la serie Fibonacci (fn): fn = Fn / 5½
Como por ejemplo, el número 40 de la serie Fibonacci es 102, 334, 155, que puede expresarse
f40 = F40 / 5½ = 102,334,155
Este método en realidad nos provee un estimado que siempre esta cerca del numero correcto Fibonacci.
http://www.iuca.net/gs/que%20es%20phi.htm
¿Qué es phi?
Phi y la serie de Fibonacci
Funciones trigonométricas
Razones matemáticas
Pentágono
Espirales Áureas
Inicio :: Ver temas relacionados: Decalogo Geometria Sagrada :: Número de Oro :: Merkaba
¿Qué es phi?
Phi (1.618033988749895... ), pronunciado como fi, es un numero irracional como Pi ( 3.14159265358979... ), pero con muchas características matemáticas inusuales. Phi es la base de la Proporción Dorada. La razón o proporción determinada por Phi (1.618...) era conocida por los Griegos como la “Sección Dorada” y por los artistas del renacimiento como la “Proporción Divina”. También se le conoce como la razón Dorada o la Proporción Áurea.
Phi, como Pi, es una razón definida por una construcción geométrica.
Pi es la relación de la circunferencia de un círculo respecto a su diámetro. Phi es la proporción de los segmentos de una línea que resultan cuando una línea es dividida de una forma única y especial.
La línea es dividida para que la proporción de la longitud de la línea entera (A) respecto a la longitud del segmento de la línea mayor (B) sea igual que la proporción de la longitud del segmento de la línea mayor (B) a la longitud del segmento de la línea menor (C)
Esto es que A es 1.618... veces B, y B es 1.618… veces C. Recíprocamente, C es 0.618... de B y B es 0.618... de A. Phi con mayúscula "Phi" es 1.6180339887..., mientras que phi con minúscula es 0.6180339887, el reciproco de Phi o Phi menos 1.
Lo que hace a phi incluso mas inusual es que puede derivarse de muchas formas y ser encontrado en proporcionalmente en el universo. Phi F puede ser derivado por: la serie numérica descubierta por Leonardo Fibonacci, matemáticas y geometría.
Phi y la serie de Fibonacci
Leonardo Fibonacci, por herencia del mundo árabe, descubrió la serie que nos lleva a phi. En el siglo XII, Leonardo Fibonacci descubrió una serie numérica simple que es la base de la increíble relación que encontramos detrás de phi. Empezando con 0 y 1, cada número de la serie es simplemente la suma de los dos anteriores. Así: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, . . .
La razón (proporción) de cada par sucesivo de números en la serie se aproxima a phi (1.618. . .). Así si dividimos 5 entre 3 es 1.666..., y 8 entre 5 es 1.60. En la medida en la que vamos mas lejos del 0 (punto de inicio de la secuencia) nos acercamos al valor de phi.
La tabla de abajo nos muestra como las proporciones de números sucesivos en la serie Fibonacci se aproxima a Phi.
Puedes computar cualquier número de la serie Fibonacci fácilmente. Usa phi para saber cualquier numero (n) de la serie Fibonacci (f)
fn = Fn / 5½
Phi puede derivarse matemáticamente resolviendo la ecuación:
n2 - n1 - n0 = 0 que es lo mismo que n2 - n - 1 = 0
Esta ecuación la rescribimos y nos queda así:
n2 = n + 1 y 1 / n = n - 1
La solución a la ecuación es la raíz cuadrada de 5 más 1 dividido entre 2
( 5½ + 1 ) / 2 = 1.6180339... = F
Esto resulta en dos propiedades únicas de phi:
Si elevas al cuadrado a phi, obtienes un numero exactamente 1 mayor que phi: 2.6180...
F2 = F + 1
Si divides a phi entre 1, obtienes un numero exactamente a 1 menos phi: 0.6180...:
1 / F = F - 1
Phi, curiosamente, puede ser expresado en cinco: 5 ^ .5 * .5 + .5 = F
Puedes usar phi para computar un número n en la serie Fibonacci (fn): fn = Fn / 5½
Como por ejemplo, el número 40 de la serie Fibonacci es 102, 334, 155, que puede expresarse
f40 = F40 / 5½ = 102,334,155
Este método en realidad nos provee un estimado que siempre esta cerca del numero correcto Fibonacci.
http://www.iuca.net/gs/que%20es%20phi.htm
|
|
|
|
|
|
LA ISLA DE PASCUA O DE RAPA NUI ESTÁ SITUADA EN UN PARALELO DE LA ESFERA TERRESTRE CUYA PROYECCIÓN A LA ESFERA CELESTE ES EL PARALELO EN EL QUE ESTÁ EL PUNTO DEL CENTRO DE LA GALAXIA
|
 First Previous 2 to 4 of 4 Next  Last |
|
|
| Reply |
Message 17 of 17 on the subject |
|
|
|
|
|
|
|
|
|
|
|
11. Proverbios 25:11 MANZANA de oro con figuras de plata Es la palabra dicha como conviene.
12. Cantares 2:5 Sustentadme con pasas, confortadme con MANZANAs; Porque estoy enferma de amor.
13. Cantares 7:8 Yo dije: Subiré a la palmera, Asiré sus ramas. Deja que tus pechos sean como racimos de vid, Y el olor de tu boca como de MANZANAs,
|
|
|
|
|
a bit of info : Vladimir Putin Confirms Russian Zombie Radiation Gun
Quote:
| Precise details have not been revealed but previous research has shown that low-frequency waves or beams can affect brain cells, alter psychological states and make it possible to transmit suggestions and commands directly into someone's thoughts. |
Principle of Correspondence ... if we humans can do it ... so can the Celestial Intelligences  ------------------- one more link   Use Harmonic Math on the following table 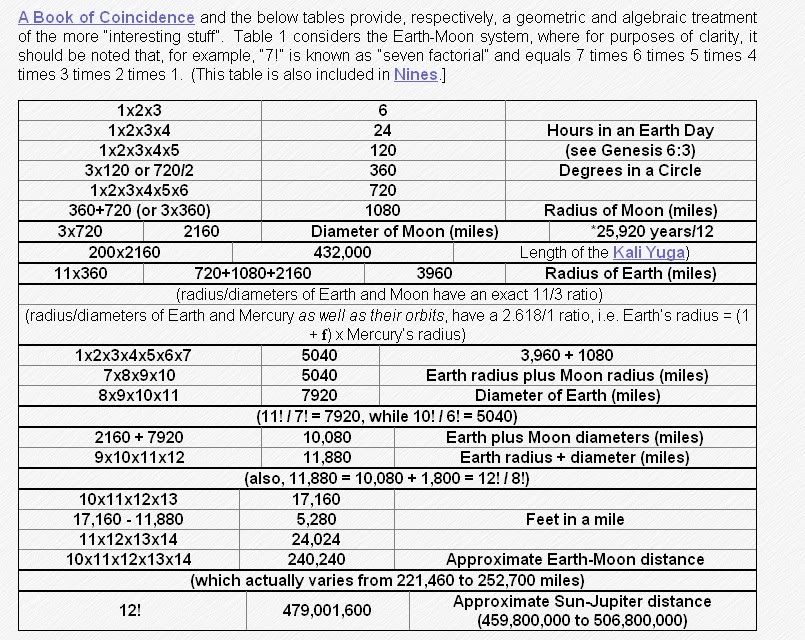  images from : The Brain is an Advanced Fractal Antenna - Page 10__________________ “Signs and symbols rule the world, not words nor laws.” - Confucius. 
|
|
|
|
|
 
1. Génesis 28:12 Y soñó: y he aquí una ESCALERA que estaba apoyada en tierra, y su extremo tocaba en el cielo; y he aquí ángeles de Dios que subían y descendían por ella.
2. 1 Reyes 6:8 La puerta del aposento de en medio estaba al lado derecho de la casa; y se subía por una ESCALERA de caracol al de en medio, y del aposento de en medio al tercero.
 
LA TORRE DE BABEL, OSEA LA UNION ENTRE EL CIELO Y LA TIERRA, ES UN "AGUJERO DE GUSANO". EN ESTE MARCO ES EL GRIAL MISMO. SIMBOLIZA LA UNION ENTRE EL CIELO Y LA TIERRA, O LA CUADRATURA DEL CIRCULO (CIRCULO=CIELO; CUADRADO=TIERRA) O LA ESCUADRA Y EL COMPAS MASONICO. ES OBVIA LA CONNOTACION CON LA "ESCALERA DE JACOB". MAGDALENA TIENE CONNOTACION CON EL MISMO TERMINO TORRE EN HEBREO.
1. Josué 15:37 Zenán, HADASA, Migdal-gad,
2. Ester 2:7 Y había criado a HADASA, es decir, Ester, hija de su tío, porque era húerfana; y la joven era de hermosa figura y de buen parecer. Cuando su padre y su madre murieron, Mardoqueo la adoptó como hija suya.
ESTHER=ISHTAR=STAR GATE=PUERTA ESTELAR
BABEL=PUERTA DE DIOS
ESCUADRA Y COMPAS MASONICO=CUADRADO / CIRCULO
1 Pedro 5:13: La iglesia que está en Babilonia, elegida juntamente con vosotros, y Marcos mi HIJO, os saludan.
HECHOS 12:12 / 33 / JUAN MARCOS
ESTRELLA DE 6 PUNTAS = 33 = 2 TRIANGULOS CRUZADOS =ALQUIMIA
3. Ezequiel 41:7 Y había mayor anchura en las cámaras de más arriba; la ESCALERA de caracol de la casa subía muy alto alrededor por dentro de la casa; por tanto, la casa tenía más anchura arriba. Del piso inferior se podía subir al de en medio, y de éste al superior.
| Reply |
Message 89 of 90 on the subject |
|
|
|
|
| Reply |
Message 90 of 90 on the subject |
|
|
|
| milky way in Simple Gematria Equals: 119 |
( |
m 13 |
i9 |
l 12 |
k 11 |
y 25 |
0 |
w 23 |
a1 |
y 25 |
) |
| queen mary in Simple Gematria Equals: 119 |
( |
q 17 |
u 21 |
e5 |
e5 |
n 14 |
0 |
m 13 |
a1 |
r 18 |
y 25 |
|
| hebrew calendar in Simple Gematria Equals: 119 |
( |
h8 |
e5 |
b2 |
r 18 |
e5 |
w 23 |
0 |
c3 |
a1 |
l 12 |
e5 |
n 14 |
d4 |
a1 |
r 18 |
| mary magdalene in Simple Gematria Equals: 119 |
( |
m 13 |
a1 |
r 18 |
y 25 |
0 |
m 13 |
a1 |
g7 |
d4 |
a1 |
l 12 |
e5 |
n 14 |
e5 |
|
|
|
|
|
|
Fibonacci Fun
Here are some illustrations by myself and others, dealing with the Fibonacci sequence and the Golden Number, Phi.
A few months ago, I noticed the exponents of Phi encode the Fibonacci sequence.
The sequence gets closer to the golden number the larger the numbers get. This will work with any two starting numbers, like say 91 and 432, for example. You’ll find the same ratio emerge if you keep adding them together. (91+432 = 523, then, 432+523=955, etc) Already we are at 1.8 to 1. (955/523) A handful more steps and we’ll have Phi to more than 99.999% accuracy.
???? If you had a million phalanges, your hand would look like King Midas.
Jain108 made a post on how, if you start with 2 and 10, you arrive at the actual numbers found in the exponents of Phi. Remember exponents are simply the number multiplied by itself n number of times. Phi cubed, or Phi to the third power, is just Phi x Phi x Phi. (1.618 x 1.618 x 1.618 = 4.236) See that was easy, now stop complaining how you’re bad at math.
Phi to the negative power is the same as saying, one divided by the Phi cubed, or whatever.
Here’s some different ways to say the same thing.
This does an excellent job of explaining where all these freaking numbers come from. (img Scott Onstott)
Circles of Fibonacci. Magenta and green cancel out and make gold
Sam Kutler found the golden number in concentric circles.
The outer ring shows the 24 digit pattern(digital roots), the inner the 60 digit pattern(last number).
Lucien Khan rediscovered the 60 digit repeat pattern.
Fibonacci Patterns
Fibonacci sequence hidden in ordinary division problem:
If you divide 1 by 999,999,999,999,999,999,999,999,999,999,999,999,999,999,999,999 (that’s 999 quattuordecillion), the Fibonacci sequence pops out.
Chad Adam’s Extended Fibonacci Series
Like I said, you can start a Fibonacci sequence with any two numbers. If you begin with the numbers 1-9, some interesting things happen.
by Chad Adams
See how the numbers match up?
The Platonic Solids
 back to the 60 digit pattern….
The Fibonacci Sequence, starting at the 60th number in the sequence. See the pattern? Just look at the last digit in each number of the sequence. [after 8 is 3 because the last digit in 13(5+8) is 3]
The Colorado State Flag
Is it just me or is Colorado’s state seal illuminaty as all hell?
Don’t even go to Denver International Airport.
I did an article on Decoding the Dollar, and found the leaves on the left side of the buck encode the fib seq. with 2,3,5,8.
The name ‘Fi-Bonacci'(Man of cheer) comes from Leonardo’s old man who could always make the town laugh.
Leonardo de Pisa, the guy we call ‘Fibonacci”, actually had his own value for π, which was 864/275, or 3.141818181818…. (Phi = 1.618..)
I talk about this more here..
The Fibonacci numbers reduced to one digit through digital parity. (21 is 3 because 2+1=3)
This is the number and sequence of numbers that God choose to use to structure all life and creation.
https://joedubs.com/fibonacci-fun/ |
|
|
|
|
I found the file of the pyramid info that Professor Scot Nelson had talked about (actually it was uploaded to a Yahoo groups file on the Rodin Cell). Although I don't agree with the findings as presented, I do believe there is some pretty amazing geometry going on with the pyramid, and it begins to explain so many of the "energy" properties that the pyramid contains. Since I have no idea how to attach files to threads (if this board even allows it) I will have to try to surmise the concept.
In short, this is the culmination of his findings. The big grid obviously represents the view of the pyramid from the top down. The symbol that he used as the "Seal of Solomon" is how he derived his findings. In short, the symbol came from the book "The Keys of Enoch" by J.J. Hurtak which had a number sequence across the top of the symbol as 1.3.1 and across the bottom as 9.1.9 with the 9's interchanging with 1's. Aside from this, the interesting thing is that the numbers of the toroid grid align perfectly with the pyramid faces, and the diagonals of the pyramid aligning perfectly with only the vertical and horizontal lines through the grid. The area I have a hard time with is calling the capstone 1. By every conceivable possibility that I see, it is definitely a 2. However, I think there is some validity to these findings as I believe the cap stone is missing from the Great Pyramid for a reason. The interesting part is that the diagonals of the pyramid are not physical properties anyway - a corner (whether inside or outside) is not really a physical object - it is an intersection. The manifestation of these numbers outside the edges of the pyramid makes more sense to me then the actual pyramid face itself. My personal thought is that the angles of the pyramid mark a boundary line so that 4 other pyramids could all touch at the apex of the Great Pyramid (for a total of 5) with each face in contact with one face of the other 4. This would create a very specific energy point at the apex, that would most likely manifest in this dimension. I believe if you take the image in the book, assume the diamond is the base of the pyramid, and the remaining pyramids make the sides of the other 4 pyramids, when they are folded along the base line of the pyramid, you are getting closer tothe interpretation of this symbol. Anyway, getting off track.... Check the numbers. There are no exceptions or mistakes. I think of interest, the numbers near the top start to create some interesting patterns, especially with the 3-9-6 and the 5. I think this is approaching the true "squaring of the circle". |
|
|
Primer
Anterior
2 a 13 de 13
Siguiente
Último
|
|
| |
|
|
©2024 - Gabitos - Todos los derechos reservados | |
|
|
Tema anterior
