|
|
General: La geometría sagrada la clave para la iluminación
Elegir otro panel de mensajes |
|
|
| De: Alcoseri (Mensaje original) |
Enviado: 18/04/2019 16:33 |
La geometría sagrada la clave para la
iluminación
Observamos modelos matemáticos detrás
de la naturaleza , de fenómenos físicos, en las
Catedrales y en los Templos Masónicos.
Ya en modelos que observas en tu
propio cuerpo , en tu propia vida o en el mundo que te rodea y que poseen esa simetría y equilibrio. Notar esos patrones que nos ayudan a desarrollar una consciencia y que
resultan ser equilibradores para nuestra
psique ya sea personal o colectivo. El flujo de darnos cuenta entre ese proceso de asimetría y simetría es
el proceso de crecimiento y evolución. La geometría sagrada nos brinda un bello
reflejo para contemplar mientras navegamos por los desafíos de la vida en busca
de equilibrio y armonía.
Ahora con el incendio de la Catedral
más famosa del Mundo , la Catedral de Notre
Dame en Paris , se rompió esa simetría en la psique colectiva del
conglomerado humano , en ese inconsciente colectivo de la Humanidad , retomarlo
será también una tarea colectiva , en la que los masones mucho tendremos que
ver, no faltará como siempre algún masón arquitecto intervenido en los trabajos
de reconstrucción, si tal como ocurrió luego del incendio de la Catedral de San
Pablo en Londres en 1666, donde masones operarios se dieron a la tarea de
reconstruirla.
"LAS MATEMÁTICAS SON EL ALFABETO
CON EL QUE DIOS ESCRIBIÓ EL UNIVERSO". ~ GALILEO
¿Qué es la geometría sagrada?
La geometría sagrada involucra
motivos sagrados universales utilizados en el diseño de todo en nuestra
realidad, con mayor frecuencia en la arquitectura, el arte y la naturaleza. La
creencia básica es que la geometría y las relaciones matemáticas, los armónicos
y las proporciones áureas también se
encuentran en la música, la luz, la cosmología. Son los patrones invisibles los
que animan nuestro mundo físico, así como las tradiciones espirituales creen
que el alma anima el cuerpo.
Las formas, los patrones y las
composiciones visuales tienen la capacidad de seducir a nuestros ojos mientras
cautivan nuestra imaginación. Ya sean obras maestras del arte o la naturaleza,
este encantamiento puede ser tan conmovedor e impresionante que las personas lo
asocian de forma natural con la trascendencia, lo sobrenatural o lo espiritual.
Bajo estos modelos se encuentran relaciones que pueden medirse, numerarse,
reproducirse y definirse. Esta área de investigación y observación, tanto
matemática como esotérica, conocida como geometría sagrada, lo iluminará y lo
desconcertará a la vez que lo invitará a cambiar su forma de ver el mundo. Con
frecuencia observamos números que se repiten constantemente , como el número
11, el 33 , el 666 entre otros, así como formas geométricas que las vemos por
todas partes , como las espirales, los cubos , los triángulos etc.
Historia de la geometría sagrada:
Las primeras culturas, incluidos
cristianos, hindúes, griegos y egipcios, reconocieron la existencia de
diferentes patrones o formas geométricas que se repiten en la naturaleza.
También establecieron que había una correlación o conexión entre los diversos
elementos encontrados en la tierra y el cielo. Estos patrones geométricos sagrados
fueron reflejados por la tierra y el cielo, y las culturas antiguas creían que
estos motivos existían en todas las partes del universo. La ciencia moderna ha
demostrado que estos patrones geométricos sagrados son las formas moleculares a veces macroscópicas a veces microscópicas
que forman la base de todas las
manifestaciones en este universo, lo vemos en las galaxias o en las neuronas
cerebrales.
Nos preguntamos ¿esto de la geometría
es realmente sagrado o es una simple manifestación de la forma?
El tema es polémico y, aunque es espiritualmente eso de
la Geometría Sagrada inspirador para
muchos, hay muchos matemáticos que desdeñan la noción de correlacionar a este geometría
con las fórmulas sagradas o místicas, la ciencia es fría , sus
datos son duros . Pero los masones , no nos basamos tanto en los
datos superficiales , vamos más allá siempre de las simples formas, y por tanto
intentaré atribuir un significado trascendental y sagrado a estos modelos, relacionarlos estos modelos con tradiciones espirituales específicas como
la Egipcia que construía Pirámides o la
Antigua Masonería Operativa que construía hermosas catedrales. ¡La simple
observación y reconocimiento de estas relaciones visuales en la naturaleza, así
como su poderosa influencia en el arte, la arquitectura y la música son más que
suficientes para dejarnos a todos sorprendidos!
Pienso que lo sagrado incluye tanto
al Caos como al Orden, a veces hay más belleza en el Caos que en el Orden ,
vemos como algo muy rígido como el Orden resulta ser en ocasiones horrible. Los foros masónicos de la internet, como Grupo Masonería de Facebook , donde todo
parece tan caótico y en ocasiones tan luminoso y ordenado , si, muchos masones
vertiendo luces , mientras otros insultan o no comprenden el sentido , da como
resultante algo sorprendente , pues ahí se refleja el carácter humano como tal.
La influencia de la geometría sagrada
se puede observar en la arquitectura de una mezquita, de una catedral , de una
pagoda o de una sinagoga.
La geometría es divertida hasta para
los niños porque implica dibujar formas utilizando papel, compas y escuadra. La
idea de que los números se representan en forma visual o a través de la música
es un ejemplo muy particular de cómo las abstracciones (números, fórmulas)
pueden reflejarse en el mundo físico. Por lo tanto, la geometría son una
ciencia interesante que se intercala entre la mente el espacio, entre la física
y la no física.
El espacio entre lo físico y lo
inmaterial suele estar reservado para el arte o la espiritualidad. Por eso es
interesante encontrar fórmulas matemáticas para cerrar la brecha. Esta es
también una de las razones por las que esta geometría en Masonería se considera "sagrada".
Alcoseri
|
|
|
|
|
August 23, 2018/

The Golden Section (aka Golden Mean, and Golden Ratio) phys.org
We use math in architecture on a daily basis to solve problems. We use it to achieve both functional and aesthetic advantages. By applying math to our architectural designs through the use of the Golden Section and other mathematical principles, we can achieve harmony and balance. As you will see from some of the examples below, the application of mathematical principles can result in beautiful and long-lasting architecture which has passed the test of time.
Using Math in Architecture for Function and Form
We use math in architecture every day at our office. For example, we use math to calculate the area of a building site or office space. Math helps us to determine the volume of gravel or soil that is needed to fill a hole. We rely on math when designing safe building structures and bridges by calculating loads and spans. Math also helps us to determine the best material to use for a structure, such as wood, concrete, or steel.
“Without mathematics there is no art.” – Luca Pacioli, De divina proportione, 1509
Architects also use math when making aesthetic decisions. For instance, we use numbers to achieve attractive proportion and harmony. This may seem counter-intuitive, but architects routinely apply a combination of math, science, and art to create attractive and functional structures. One example of this is when we use math to achieve harmony and proportion by applying a well-known principle called the Golden Section
Math and Proportion – The Golden Section

Perfect proportions of the human body – The Vitruvian Man – by Leonardo da Vinci.
We tend to think of beauty as purely subjective, but that is not necessarily the case. There is a relationship between math and beauty. By applying math to our architectural designs through the use of the Golden Section and other mathematical principles, we can achieve harmony and balance.
The Golden Section is one example of a mathematical principle that is believed to result in pleasing proportions. It was mentioned in the works of the Greek mathematician Euclid, the father of geometry. Since the 4th century, artists and architects have applied the Golden Section to their work.
The Golden Section is a rectangular form that, when cut in half or doubled, results in the same proportion as the original form. The proportions are 1: the square root of 2 (1.414) It is one of many mathematical principles that architects use to bring beautiful proportion to their designs.
Examples of the Golden Section are found extensively in nature, including the human body. The influential author Vitruvius asserted that the best designs are based on the perfect proportions of the human body.
Over the years many well-known artists and architects, such as Leonardo da Vinci and Michelangelo, used the Golden Section to define the dimensions and proportions in their works. For example, you can see the Golden Section demonstrated in DaVinci’s painting Mona Lisa and his drawing Vitruvian Man.
Famous Buildings Influenced by Mathematical Principles
Here are some examples of famous buildings universally recognized for their beauty. We believe their architects used math and the principals of the Golden Section in their design:
Parthenon
The classical Doric columned Parthenon was built on the Acropolis between 447 and 432 BC. It was designed by the architects Iktinos and Kallikrates. The temple had two rooms to shelter a gold and ivory statue of the goddess Athena and her treasure. Visitors to the Parthenon viewed the statue and temple from the outside. The refined exterior is recognized for its proportional harmony which has influenced generations of designers. The pediment and frieze were decorated with sculpted scenes of Athena, the Gods, and heroes.

Parthenon Golden Section
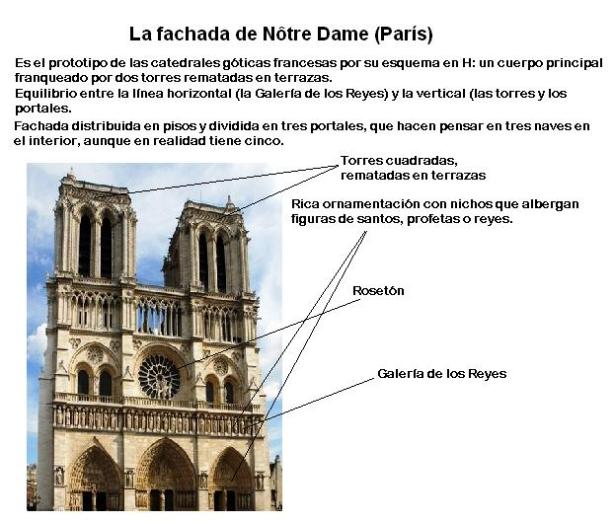
Notre Dame Cathedral in Paris
Built on the Ile de la Cite, Notre Dame was built on the site of two earlier churches. The foundation stone was laid by Pope Alexander III in 1163. The stone building demonstrates various styles of architecture, due to the fact that construction occurred for over 300 years. It is predominantly French Gothic, but also has elements of Renaissance and Naturalism. The cathedral interior is 427 feet x 157 feet in plan. The two Gothic towers on the west façade are 223 feet high. They were intended to be crowned by spires, but the spires were never built. The cathedral is especially loved for its three stained glass rose windows and daring flying buttresses. During the Revolution, the building was extensively damaged and was saved from demolition by the emperor Napoleon.

Notre Dame Cathedral in Paris
Taj Mahal
Built in Agra between 1631 and 1648, the Taj Mahal is a white marble mausoleum designed by Ustad-Ahmad Lahori. This jewel of Indian architecture was built by Emperor Shah Jahan in memory of his favorite wife. Additional buildings and elements were completed in 1653. The square tomb is raised and is dramatically located at the end of a formal garden. On the interior, the tomb chamber is octagonal and is surrounded by hallways and four corner rooms. Building materials are brick and lime veneered with marble and sandstone.

Taj Mahal designed by Ustad-Ahmad Lahori
As you can see from the above examples, the application of mathematical principles can result in some pretty amazing architecture. The architects’ work reflects eye-catching harmony and balance. Although these buildings are all quite old, their designs have pleasing proportions which have truly passed the test of time.
https://bleckarchitects.com/math-in-architecture/
|
|
|
|
|
|

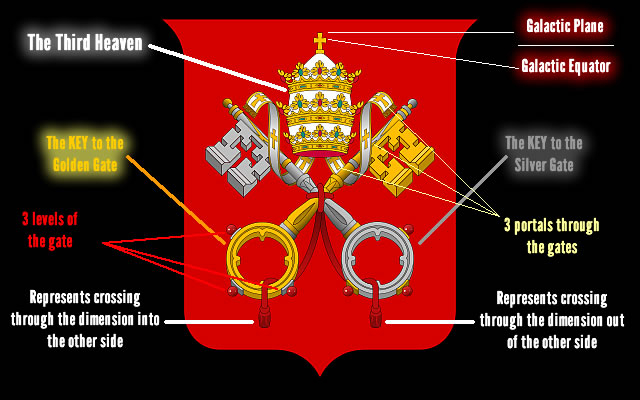
LLAVE DE ORO Y DE PLATA AL IGUAL QUE LA MANZANA
Incendio Notre Dame: Última hora de la catedral de París (15 DE ABRIL)

 Incendio Notre Dame (París), en directo (Bertrand Guay / AFP)
PHI A NOTRE-DAME
A la catredal de Notre Dame hi observem més rectanlges auris: Creat per Mario Pastor 
The DaVinci Code, Notre Dame Cathedral from DaVinci Code
original movie prop
 
        

August 23, 2018/

The Golden Section (aka Golden Mean, and Golden Ratio) phys.org
We use math in architecture on a daily basis to solve problems. We use it to achieve both functional and aesthetic advantages. By applying math to our architectural designs through the use of the Golden Section and other mathematical principles, we can achieve harmony and balance. As you will see from some of the examples below, the application of mathematical principles can result in beautiful and long-lasting architecture which has passed the test of time.
Using Math in Architecture for Function and Form
We use math in architecture every day at our office. For example, we use math to calculate the area of a building site or office space. Math helps us to determine the volume of gravel or soil that is needed to fill a hole. We rely on math when designing safe building structures and bridges by calculating loads and spans. Math also helps us to determine the best material to use for a structure, such as wood, concrete, or steel.
“Without mathematics there is no art.” – Luca Pacioli, De divina proportione, 1509
Architects also use math when making aesthetic decisions. For instance, we use numbers to achieve attractive proportion and harmony. This may seem counter-intuitive, but architects routinely apply a combination of math, science, and art to create attractive and functional structures. One example of this is when we use math to achieve harmony and proportion by applying a well-known principle called the Golden Section
Math and Proportion – The Golden Section

Perfect proportions of the human body – The Vitruvian Man – by Leonardo da Vinci.
We tend to think of beauty as purely subjective, but that is not necessarily the case. There is a relationship between math and beauty. By applying math to our architectural designs through the use of the Golden Section and other mathematical principles, we can achieve harmony and balance.
The Golden Section is one example of a mathematical principle that is believed to result in pleasing proportions. It was mentioned in the works of the Greek mathematician Euclid, the father of geometry. Since the 4th century, artists and architects have applied the Golden Section to their work.
The Golden Section is a rectangular form that, when cut in half or doubled, results in the same proportion as the original form. The proportions are 1: the square root of 2 (1.414) It is one of many mathematical principles that architects use to bring beautiful proportion to their designs.
Examples of the Golden Section are found extensively in nature, including the human body. The influential author Vitruvius asserted that the best designs are based on the perfect proportions of the human body.
Over the years many well-known artists and architects, such as Leonardo da Vinci and Michelangelo, used the Golden Section to define the dimensions and proportions in their works. For example, you can see the Golden Section demonstrated in DaVinci’s painting Mona Lisa and his drawing Vitruvian Man.
Famous Buildings Influenced by Mathematical Principles
Here are some examples of famous buildings universally recognized for their beauty. We believe their architects used math and the principals of the Golden Section in their design:
Parthenon
The classical Doric columned Parthenon was built on the Acropolis between 447 and 432 BC. It was designed by the architects Iktinos and Kallikrates. The temple had two rooms to shelter a gold and ivory statue of the goddess Athena and her treasure. Visitors to the Parthenon viewed the statue and temple from the outside. The refined exterior is recognized for its proportional harmony which has influenced generations of designers. The pediment and frieze were decorated with sculpted scenes of Athena, the Gods, and heroes.

Parthenon Golden Section
Notre Dame Cathedral in Paris
Built on the Ile de la Cite, Notre Dame was built on the site of two earlier churches. The foundation stone was laid by Pope Alexander III in 1163. The stone building demonstrates various styles of architecture, due to the fact that construction occurred for over 300 years. It is predominantly French Gothic, but also has elements of Renaissance and Naturalism. The cathedral interior is 427 feet x 157 feet in plan. The two Gothic towers on the west façade are 223 feet high. They were intended to be crowned by spires, but the spires were never built. The cathedral is especially loved for its three stained glass rose windows and daring flying buttresses. During the Revolution, the building was extensively damaged and was saved from demolition by the emperor Napoleon.

Notre Dame Cathedral in Paris
Taj Mahal
Built in Agra between 1631 and 1648, the Taj Mahal is a white marble mausoleum designed by Ustad-Ahmad Lahori. This jewel of Indian architecture was built by Emperor Shah Jahan in memory of his favorite wife. Additional buildings and elements were completed in 1653. The square tomb is raised and is dramatically located at the end of a formal garden. On the interior, the tomb chamber is octagonal and is surrounded by hallways and four corner rooms. Building materials are brick and lime veneered with marble and sandstone.

Taj Mahal designed by Ustad-Ahmad Lahori
As you can see from the above examples, the application of mathematical principles can result in some pretty amazing architecture. The architects’ work reflects eye-catching harmony and balance. Although these buildings are all quite old, their designs have pleasing proportions which have truly passed the test of time.
https://bleckarchitects.com/math-in-architecture/
|
|
|
|
|
 Primer
Primer
 Anterior
2 a 4 de 19
Siguiente
Anterior
2 a 4 de 19
Siguiente Último
Último
|
|
| |
|
|
©2024 - Gabitos - Todos los derechos reservados | |
|
|




































 Incendio Notre Dame (París), en directo (Bertrand Guay / AFP)
Incendio Notre Dame (París), en directo (Bertrand Guay / AFP)










