|
|
General: CUBO=NUEVA JERUSALEN=TABERNACULO=LADO X LADO X LADO=MARTE/MARCOS/GRIAL
Elegir otro panel de mensajes |
|
|
https://es.wikipedia.org/wiki/Albert_Einstein
Albert Einstein (en alemán [ˈalbɛɐ̯t ˈaɪnʃtaɪn]; Ulm, Imperio alemán, 14 de marzo de ... En 1915 presentó la teoría de la relatividad general, en la que reformuló por completo el concepto de gravedad. ...... Einstein, Albert (1905e) [manuscrito recibido 27 de septiembre 1905], «Ist die Trägheit eines Körpers von seinem ...
rpp.pe › Lima
27 sep. 2015 - ... primera vez su Teoría de la Relatividad Especial, también llamada restringida; y en 1960, muere el ... 27 de septiembre del 2015 - 12:01 AM ...
ar.tuhistory.com/etiquetas/teoria-de-la-relatividad
Albert Einstein publica la teoría general de la relatividad ... De la teoría especial de la relatividad se deduce su famosa ecuación E=mc2, ... 27-09-1905 D.C..
https://www.gabitos.com/DESENMASCARANDO_LAS_FALSAS.../template.php?...
7 ene. 2014 - En 1905 Einstein publicó su teoría de la relatividad especial, que ...... Einstein presentó a los editores de Annalen el 27 de septiembre del ...
MATT 16:18 is an in your face glyph for the golden mean ratio 1.618
(“MATT” is pun of “MATTER”)
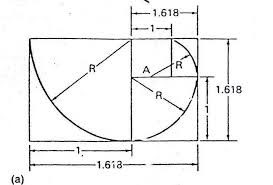
Golden Mean ratio of 1.618
The Golden Mean and the Equilateral Triangle in a Circle; THE CRUCIAL FACT IS THE MIDPOINT OF THE TRIANGLE SIDE
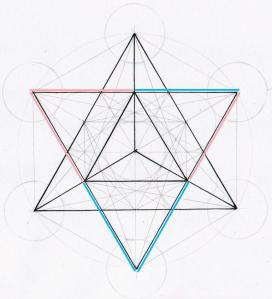
Star Tetrahedron, formed by the MIDPOINTS OF THE CENTRAL EQUILATERAL TRIANGLE (the blue and rose colored lines indicate these midpoint halves)
Saint Mary Magdalene in Venice
 A closer look 
 the Apple
|
|
|
|
|
|
1/10/2019
the Apple
|
|
|
|
|
|
|
|
3 Phi and Triangles
3.1 Phi and the Equilateral Triangle
 Chris and Penny at Regina University's Math Central (Canada) show how we can use any circle to construct on it a hexagon and an equilateral triangle. Joining three pairs of points then reveals a line and its golden section point as follows:
- On any circle (centre O), construct the 6 equally spaced points A, B, C, D, E and F on its circumference without altering your compasses, so they are the same distance apart as the radius of the circle. ABCDEF forms a regular hexagon.
- Choose every other point to make an equilateral triangle ACE.
- On two of the sides of that triangle (AE and AC), mark their mid-points P and Q by joining the centre O to two of the unused points of the hexagon (F and B).
- The line PQ is then extended to meet the circle at point R.
Q is the golden section point of the line PR.
 Q is a gold point of PRThe proof of this is left to you because it is a nice exercise either using coordinate geometry and the equation of the circle and the line PQ to find their point of intersection or else using plane geometry to find the lengths PR and QR.
The diagram on the left has many golden sections and yet contains only equilateral triangles. Can you make your own design based on this principle?
Chris and Penny's page shows how to continue using your compasses to make a pentagon with QR as one side.
- Equilateral Triangles and the Golden ratio J F Rigby, Mathematical Gazette vol 72 (1988), pages 27-30.
http://www.maths.surrey.ac.uk/hosted-sites/R.Knott/Fibonacci/phi2DGeomTrig.html |
|
|
 Primer
Anterior
27 a 41 de 71
Siguiente
Último
|
|
| |
|
|
©2024 - Gabitos - Todos los derechos reservados | |
|
|
