|
|
General: NUMERO 144=12*12=SEXTO DIA (144 HORAS)=NUEVA JERUSALEN=12 DE LA SERIE FIBONACCI
Triar un altre plafó de missatges |
|
|
 
11 DE SEPTIEMBRE O SEPTIEMBRE 11
11/9 O 9/11
Sapientia Aedificavit Sibi Domum. Es decir, "la sabiduría ha edificado aquí su casa". Resulta curioso que la misma frase aparece en el Evangelio de María Magdalena, un texto apócrifo. Se dice que en el interior de esta iglesia y de otras muchas de Venecia está escondido el tesoro de los templarios. Pero no hay ninguna prueba de ello. Para terminar ya con esta entrada me gustaría que nos acercásemos un momento a uno de los edificios más emblemáticos de Venecia: el Palacio Ducal.

La Maddalena

La Maddalena

Tomb of Tommaso Temanza

ISLA SAN GIORGIO (VENECIA)=GEORGE LEMAITRE
GEMATRIA EN INGLES DE SEED=33
GEMATRIA EN INGLES DE GATE=33
SARA (CE-SAREA DE FILIPO)=PARALELO 33
"¡Oh profundidad de las riquezas de la sabiduría (sophia)
y de la ciencia (gnwsiV, gnosis) de Dios!
¡Cuán incomprensibles son sus juicios, e inescrutables sus caminos!"
(Romanos, 11: 33).
 the Apple
| milky way in Simple Gematria Equals: 119 |
( |
m 13 |
i9 |
l 12 |
k 11 |
y 25 |
0 |
w 23 |
a1 |
y 25 |
) |
| queen mary in Simple Gematria Equals: 119 |
( |
q 17 |
u 21 |
e5 |
e5 |
n 14 |
0 |
m 13 |
a1 |
r 18 |
y 25 |
|
| hebrew calendar in Simple Gematria Equals: 119 |
( |
h8 |
e5 |
b2 |
r 18 |
e5 |
w 23 |
0 |
c3 |
a1 |
l 12 |
e5 |
n 14 |
d4 |
a1 |
r 18 |
| mary magdalene in Simple Gematria Equals: 119 |
( |
m 13 |
a1 |
r 18 |
y 25 |
0 |
m 13 |
a1 |
g7 |
d4 |
a1 |
l 12 |
e5 |
n 14 |
e5 |
|

|
|
|
|
|
EL DIA 22 DE JULIO, ES EL DIA NUMERO 203 GREGORIANO Y EL DIA NUMERO 144 DESDE EL PRIMERO DE MARZO, ANTIGUO AÑO NUEVO. ES CURIOSO QUE EL DIA DE LA ASUNCION, OSEA EL 15 DE AGOSTO, ES EL DIA 227 GREGORIANO, CUANDO NO ES BISIESTO, PERO ES EL DIA NUMERO 168 DESDE EL PRIMERO DE MARZO.
144=6*24
168=7*24
ES OBVIO EL NEXO CON EL RELOJ
|
|
|
|
|
|
|
|
JERUSALEN ESTABA EN LA TRIBU DE BENJAMIN, OSEA QUE ES OBVIO QUE LA NUEVA JERUSALEN ES PABLO MISMO
PABLO/PEQUEÑO/PERRO/LOBO/GUERRA/MARTE/GRIAL
PABLO ES UN TIPO DEL GRIAL MISMO
16. Génesis 49:27 Benjamín es lobo arrebatador; A la mañana comerá la presa, Y a la tarde repartirá los despojos.
169. Romanos 11:1 Digo, pues: ¿Ha desechado Dios a su pueblo? En ninguna manera. Porque también yo soy israelita, de la descendencia de Abraham, de la tribu de Benjamín. 170. Filipenses 3:5 circuncidado al octavo día, del linaje de Israel, de la tribu de Benjamín, hebreo de hebreos; en cuanto a la ley, fariseo;
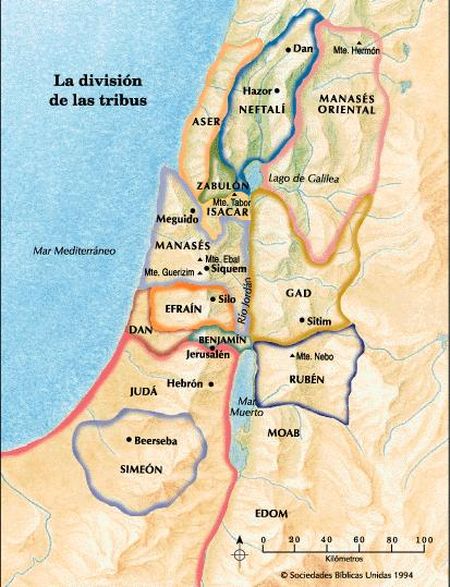 LAS DOCE TRIBUS DE ISRAEL LAS DOCE TRIBUS DE ISRAEL
|
|
|
|
|
|
|
|
Sabemos que Vesica Piscis esta en funcion al a los 153 peces de Juan 21:11.
 Aqui tenemos a Pi - la circunferencia del toro y la vesica piscis 256/153 equivalente a la raiz cuadrada de 3 En el hipercubo las coordinadas binarias de Piscis son decimal 3 y binario 11 153 los pescados de Jesus en la biblia
Sapientia Aedificavit Sibi Domum. Es decir, "la sabiduría ha edificado aquí su casa". Resulta curioso que la misma frase aparece en el Evangelio de María Magdalena, un texto apócrifo. Se dice que en el interior de esta iglesia y de otras muchas de Venecia está escondido el tesoro de los templarios. Pero no hay ninguna prueba de ello. Para terminar ya con esta entrada me gustaría que nos acercásemos un momento a uno de los edificios más emblemáticos de Venecia: el Palacio Ducal.
|
|
|
|
|



|

LLAVE DE ORO Y DE PLATA AL IGUAL QUE LA MANZANA
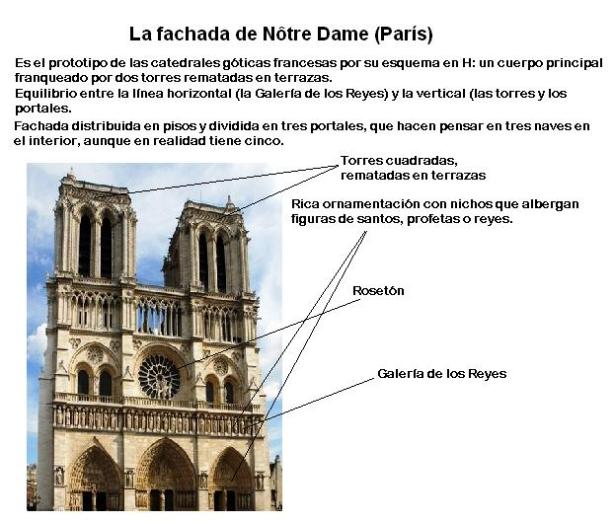
Incendio Notre Dame: Última hora de la catedral de París (15 DE ABRIL)

 Incendio Notre Dame (París), en directo (Bertrand Guay / AFP)
PHI A NOTRE-DAME
A la catredal de Notre Dame hi observem més rectanlges auris: Creat per Mario Pastor 
The DaVinci Code, Notre Dame Cathedral from DaVinci Code
original movie prop
 
        

August 23, 2018/

The Golden Section (aka Golden Mean, and Golden Ratio) phys.org
We use math in architecture on a daily basis to solve problems. We use it to achieve both functional and aesthetic advantages. By applying math to our architectural designs through the use of the Golden Section and other mathematical principles, we can achieve harmony and balance. As you will see from some of the examples below, the application of mathematical principles can result in beautiful and long-lasting architecture which has passed the test of time.
Using Math in Architecture for Function and Form
We use math in architecture every day at our office. For example, we use math to calculate the area of a building site or office space. Math helps us to determine the volume of gravel or soil that is needed to fill a hole. We rely on math when designing safe building structures and bridges by calculating loads and spans. Math also helps us to determine the best material to use for a structure, such as wood, concrete, or steel.
“Without mathematics there is no art.” – Luca Pacioli, De divina proportione, 1509
Architects also use math when making aesthetic decisions. For instance, we use numbers to achieve attractive proportion and harmony. This may seem counter-intuitive, but architects routinely apply a combination of math, science, and art to create attractive and functional structures. One example of this is when we use math to achieve harmony and proportion by applying a well-known principle called the Golden Section
Math and Proportion – The Golden Section

Perfect proportions of the human body – The Vitruvian Man – by Leonardo da Vinci.
We tend to think of beauty as purely subjective, but that is not necessarily the case. There is a relationship between math and beauty. By applying math to our architectural designs through the use of the Golden Section and other mathematical principles, we can achieve harmony and balance.
The Golden Section is one example of a mathematical principle that is believed to result in pleasing proportions. It was mentioned in the works of the Greek mathematician Euclid, the father of geometry. Since the 4th century, artists and architects have applied the Golden Section to their work.
The Golden Section is a rectangular form that, when cut in half or doubled, results in the same proportion as the original form. The proportions are 1: the square root of 2 (1.414) It is one of many mathematical principles that architects use to bring beautiful proportion to their designs.
Examples of the Golden Section are found extensively in nature, including the human body. The influential author Vitruvius asserted that the best designs are based on the perfect proportions of the human body.
Over the years many well-known artists and architects, such as Leonardo da Vinci and Michelangelo, used the Golden Section to define the dimensions and proportions in their works. For example, you can see the Golden Section demonstrated in DaVinci’s painting Mona Lisa and his drawing Vitruvian Man.
Famous Buildings Influenced by Mathematical Principles
Here are some examples of famous buildings universally recognized for their beauty. We believe their architects used math and the principals of the Golden Section in their design:
Parthenon
The classical Doric columned Parthenon was built on the Acropolis between 447 and 432 BC. It was designed by the architects Iktinos and Kallikrates. The temple had two rooms to shelter a gold and ivory statue of the goddess Athena and her treasure. Visitors to the Parthenon viewed the statue and temple from the outside. The refined exterior is recognized for its proportional harmony which has influenced generations of designers. The pediment and frieze were decorated with sculpted scenes of Athena, the Gods, and heroes.

Parthenon Golden Section
Notre Dame Cathedral in Paris
Built on the Ile de la Cite, Notre Dame was built on the site of two earlier churches. The foundation stone was laid by Pope Alexander III in 1163. The stone building demonstrates various styles of architecture, due to the fact that construction occurred for over 300 years. It is predominantly French Gothic, but also has elements of Renaissance and Naturalism. The cathedral interior is 427 feet x 157 feet in plan. The two Gothic towers on the west façade are 223 feet high. They were intended to be crowned by spires, but the spires were never built. The cathedral is especially loved for its three stained glass rose windows and daring flying buttresses. During the Revolution, the building was extensively damaged and was saved from demolition by the emperor Napoleon.

Notre Dame Cathedral in Paris
Taj Mahal
Built in Agra between 1631 and 1648, the Taj Mahal is a white marble mausoleum designed by Ustad-Ahmad Lahori. This jewel of Indian architecture was built by Emperor Shah Jahan in memory of his favorite wife. Additional buildings and elements were completed in 1653. The square tomb is raised and is dramatically located at the end of a formal garden. On the interior, the tomb chamber is octagonal and is surrounded by hallways and four corner rooms. Building materials are brick and lime veneered with marble and sandstone.

Taj Mahal designed by Ustad-Ahmad Lahori
As you can see from the above examples, the application of mathematical principles can result in some pretty amazing architecture. The architects’ work reflects eye-catching harmony and balance. Although these buildings are all quite old, their designs have pleasing proportions which have truly passed the test of time.
https://bleckarchitects.com/math-in-architecture/
|
|
|
|
|
|
|
Fibonacci 24 Repeating Pattern
May 15, 2012 by Gary Meisner
The Fibonacci sequence has a pattern that repeats every 24 numbers.
Numeric reduction is a technique used in analysis of numbers in which all the digits of a number are added together until only one digit remains. As an example, the numeric reduction of 256 is 4 because 2+5+6=13 and 1+3=4.
Applying numeric reduction to the Fibonacci series produces an infinite series of 24 repeating digits:
1, 1, 2, 3, 5, 8, 4, 3, 7, 1, 8, 9, 8, 8, 7, 6, 4, 1, 5, 6, 2, 8, 1, 9
If you take the first 12 digits and add them to the second twelve digits and apply numeric reduction to the result, you find that they all have a value of 9.
| 1st 12 numbers |
1 |
1 |
2 |
3 |
5 |
8 |
4 |
3 |
7 |
1 |
8 |
9 |
| 2nd 12 numbers |
8 |
8 |
7 |
6 |
4 |
1 |
5 |
6 |
2 |
8 |
1 |
9 |
| Numeric reduction – Add rows 1 and 2 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
18 |
| Final numeric reduction – Add digits of result |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
This pattern was contributed both by Joseph Turbeville and then again by a mathematician by the name of Jain.
We would expect a pattern to exist in the Fibonacci series since each number in the series encodes the sum of the previous two. What’s not quite so obvious is why this pattern should repeat every 24 numbers or why the first and last half of the series should all add to 9.
For those of you from the “Show Me” state, this pattern of 24 digits is demonstrated in the numeric reduction of the first 73 numbers of the Fibonacci series, as shown below:
|
Fibonacci Number
|
Numeric reduction by adding digits |
| 1st Level |
2nd Level |
Final Level |
| Example: 2,584 |
2+5+8+4=19 |
1+9=10 |
1+0=1 |
| 0 |
0 |
0 |
0 |
| 1 |
1 |
1 |
1 |
| 1 |
1 |
1 |
1 |
| 2 |
2 |
2 |
2 |
| 3 |
3 |
3 |
3 |
| 5 |
5 |
5 |
5 |
| 8 |
8 |
8 |
8 |
| 13 |
4 |
4 |
4 |
| 21 |
3 |
3 |
3 |
| 34 |
7 |
7 |
7 |
| 55 |
10 |
1 |
1 |
| 89 |
17 |
8 |
8 |
| 144 |
9 |
9 |
9 |
| 233 |
8 |
8 |
8 |
| 377 |
17 |
8 |
8 |
| 610 |
7 |
7 |
7 |
| 987 |
24 |
6 |
6 |
| 1,597 |
22 |
4 |
4 |
| 2,584 |
19 |
10 |
1 |
| 4,181 |
14 |
5 |
5 |
| 6,765 |
24 |
6 |
6 |
| 10,946 |
20 |
2 |
2 |
| 17,711 |
17 |
8 |
8 |
| 28,657 |
28 |
10 |
1 |
| 46,368 |
27 |
9 |
9 |
| 75,025 |
19 |
10 |
1 |
| 121,393 |
19 |
10 |
1 |
| 196,418 |
29 |
11 |
2 |
| 317,811 |
21 |
3 |
3 |
| 514,229 |
23 |
5 |
5 |
| 832,040 |
17 |
8 |
8 |
| 1,346,269 |
31 |
4 |
4 |
| 2,178,309 |
30 |
3 |
3 |
| 3,524,578 |
34 |
7 |
7 |
| 5,702,887 |
37 |
10 |
1 |
| 9,227,465 |
35 |
8 |
8 |
| 14,930,352 |
27 |
9 |
9 |
| 24,157,817 |
35 |
8 |
8 |
| 39,088,169 |
44 |
8 |
8 |
| 63,245,986 |
43 |
7 |
7 |
| 102,334,155 |
24 |
6 |
6 |
| 165,580,141 |
31 |
4 |
4 |
| 267,914,296 |
46 |
10 |
1 |
| 433,494,437 |
41 |
5 |
5 |
| 701,408,733 |
33 |
6 |
6 |
| 1,134,903,170 |
29 |
11 |
2 |
| 1,836,311,903 |
35 |
8 |
8 |
| 2,971,215,073 |
37 |
10 |
1 |
| 4,807,526,976 |
54 |
9 |
9 |
| 7,778,742,049 |
55 |
10 |
1 |
| 12,586,269,025 |
46 |
10 |
1 |
| 20,365,011,074 |
29 |
11 |
2 |
| 32,951,280,099 |
48 |
12 |
3 |
| 53,316,291,173 |
41 |
5 |
5 |
| 86,267,571,272 |
53 |
8 |
8 |
| 139,583,862,445 |
58 |
13 |
4 |
| 225,851,433,717 |
48 |
12 |
3 |
| 365,435,296,162 |
52 |
7 |
7 |
| 591,286,729,879 |
73 |
10 |
1 |
| 956,722,026,041 |
44 |
8 |
8 |
| 1,548,008,755,920 |
54 |
9 |
9 |
| 2,504,730,781,961 |
53 |
8 |
8 |
| 4,052,739,537,881 |
62 |
8 |
8 |
| 6,557,470,319,842 |
61 |
7 |
7 |
| 10,610,209,857,723 |
51 |
6 |
6 |
| 17,167,680,177,565 |
67 |
13 |
4 |
| 27,777,890,035,288 |
73 |
10 |
1 |
| 44,945,570,212,853 |
59 |
14 |
5 |
| 72,723,460,248,141 |
51 |
6 |
6 |
| 117,669,030,460,994 |
65 |
11 |
2 |
| 190,392,490,709,135 |
62 |
8 |
8 |
| 308,061,521,170,129 |
46 |
10 |
1 |
| 498,454,011,879,264 |
72 |
9 |
9 |
Thanks to Joseph Turbeville for sending “A Glimmer of Light from the Eye of a Giant” and to Helga Hertsig for bringing Jain’s discovery of this pattern to my attention.
Filed Under: Math
https://www.goldennumber.net/fibonacci-24-pattern/ |
|
|
|
|


https://es.wikipedia.org/wiki/Albert_Einstein
Albert Einstein (en alemán [ˈalbɛɐ̯t ˈaɪnʃtaɪn]; Ulm, Imperio alemán, 14 de marzo de ... En 1915 presentó la teoría de la relatividad general, en la que reformuló por completo el concepto de gravedad. ...... Einstein, Albert (1905e) [manuscrito recibido 27 de septiembre 1905], «Ist die Trägheit eines Körpers von seinem ...
rpp.pe › Lima
27 sep. 2015 - ... primera vez su Teoría de la Relatividad Especial, también llamada restringida; y en 1960, muere el ... 27 de septiembre del 2015 - 12:01 AM ...
ar.tuhistory.com/etiquetas/teoria-de-la-relatividad
Albert Einstein publica la teoría general de la relatividad ... De la teoría especial de la relatividad se deduce su famosa ecuación E=mc2, ... 27-09-1905 D.C..
https://www.gabitos.com/DESENMASCARANDO_LAS_FALSAS.../template.php?...
7 ene. 2014 - En 1905 Einstein publicó su teoría de la relatividad especial, que ...... Einstein presentó a los editores de Annalen el 27 de septiembre del ...
MATT 16:18 is an in your face glyph for the golden mean ratio 1.618
(“MATT” is pun of “MATTER”)
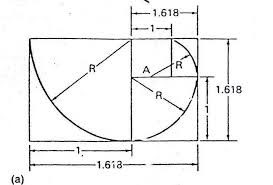
Golden Mean ratio of 1.618

The Golden Mean and the Equilateral Triangle in a Circle; THE CRUCIAL FACT IS THE MIDPOINT OF THE TRIANGLE SIDE
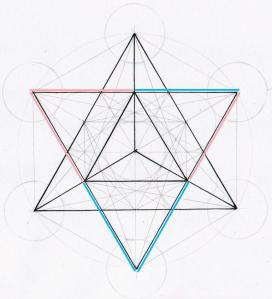
Star Tetrahedron, formed by the MIDPOINTS OF THE CENTRAL EQUILATERAL TRIANGLE (the blue and rose colored lines indicate these midpoint halves)
Saint Mary Magdalene in Venice
 A closer look 
 the Apple
|
|
|
 Primer Primer
 Anterior
56 a 70 de 85
Següent Anterior
56 a 70 de 85
Següent Darrer
Darrer
|
|
| |
|
|
©2025 - Gabitos - Tots els drets reservats | |
|
|

