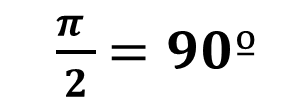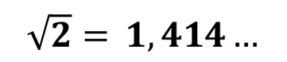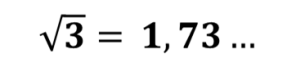Número 11, atentados de Oslo y Matemáticas Áureas
Ciertamente uno podría decir que existen demasiadas casualidades respecto a eventos catastróficos y la ocurrencia del número 11. Algunos de los últimos ejemplos nos remiten al gran terremoto de Sumatra, de 8,7 grados en la escala Richter, acaecido el pasado 11 de abril de este mismo 2012 y al terremoto y tsunami de Fukushima del 11 de marzo de 2011, que llegó a 9 de intensidad en la misma escala.
Vídeo sobre la la increible historia del número 11
Especialmente interesante son los datos que respectan a los atentados de Oslo. Los hechos sucedieron el día 22 de julio de 2011. Si comenzamos analizando la fecha hay algo que salta a la vista:
22 es múltiplo de 11 = 11+11 = 11×2
Además si tenemos en cuenta el día y el mes, tenemos:
Día= 22, mes=7
2+2+7 = 11 otra vez.
Hay otro detalle que se le ha escapado a la mayoría, pero que es de una importancia capital, ya que como pretendo establecer en este artículo, el uso del número 11 va asociado a números irracionales y trascendentales, como son Pi y Phi.
Pi= 3,14159265…
Phi= 1,618033988…
Los números irracionales son números especiales, ya que no pueden ser expresados con una fracción de números enteros y cuando además son trascendentales, es porque tienen un número de decimales no consecutivos infinito (es el caso de Phi y de Pi).
En realidad desde el prisma de las matemáticas áureas, he decidido nombrarlos números generatrices, ya que dichos números están intrínsecamente implicados, en la generación de lo que comúnmente denominamos realidad. Dicho de otra manera, sus propiedades matemáticas los sitúan en el centro de la matriz de generación de la realidad fractal.
Además tienen una propiedad maravillosa y es que después de la coma, literalmente generan infinitas combinaciones de números. Son como el motor que proyecta la realidad fractal hacia el infinito.
Volviendo al ejemplo de Oslo, si nos fijamos atentamente, los atentado sucedieron el día 22 del mes 7. Una de las aproximaciones históricas más conocidas del número Pi, que como sabéis define las propiedades no solo de la circunferencia, si no también de la esfera entre otras; implica precisamente a 22 y a 7, de forma que:
Una de las primeras referencias escritas de esta aproximación fraccionaria de Pi es el Papiro de Rhind. Un papiro de ejercicios matemáticos que data del antiguo Egipto, aunque no es la única manifestación. En los antiguos escritos védicos de la India, se habla del uso de una antigua escala musical que constaba de 7 tonos principales y de 22 semitonos o srutis.
Esto aunque pueda sonar chocante tiene una lógica aplastante, ya que la música y las resonancias armónicas en la que estos números especiales intervienen, son manifestaciones del mismo fenómeno, energía y esta se distribuye siguiendo las mismas matemáticas.
Otro ejemplo paradigmático fue Pitágoras, que además de matemático y filósofo, estudio en profundidad las armonías musicales y como estas proporciones matemáticas armónicas se aplicaban al Cosmos.
Volvemos a resituarnos en los lamentables sucesos de Oslo y aparte de la fecha me gustaría destacar dos detalles más que son tremendamente significativos. El número oficial de víctimas de los atentados acabó ascendiendo hasta 77. Para empezar este número por sí solo es múltiplo de 11. En concreto es:
11×7 = 77
Cabe destacar que otra vez tenemos una referencia aludida al número Pi, ya que:
No solo eso, si tomamos el recorrido en la circunferencia de Pi medios, obtenemos la medida de 90º, que describe la forma geométrica del ángulo recto que caracteriza al cuadrado, que también relaciona el próximo número irracional.
El siguiente número irracional, la raíz cuadrada de 2, que es fundamental, ya que determina la longitud de la diagonal de un cuadrado de lado 1:
7+7 = 14
Tenemos que la raíz de 2 y su inverso:
Es cuando sumamos el número oficial de heridos en los atentados, con el número de víctimas, que aparece el tercer actor de la obra, la raíz cuadrada de 3.
Heridos = 96
Víctimas = 77
Total = 96+77 = 173
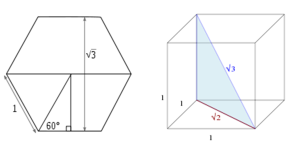
Estas relaciones matemáticas son esenciales, ya que la raíz de 3 determina la longitud de la diagonal que une vértices opuestos y que por lo tanto determina la tridimensionalidad de un cubo o hexaedro de lado 1 y la distancia entre los lados de un hexágono.
Si unimos los tres números irracionales que hemos encontrado, aparece de forma natural la intersección de las circunferencias, la Vésica Piscis. La base de la matriz geométrica y matemática de generación de la realidad fractal.
Descubre mucho más sobre como funcionan las Matemáticas Áureas y como se han codificado a nivel histórico este conocimiento en el seminario del próximo 1 de julio.