|
|
General: TEMPLO DE EZEQUIEL=MAQUINA DEL TIEMPO=HIPERCUBO
Triar un altre plafó de missatges |
|
|
lo que quiero demostrar con todo esto es que la biblia es un libro mistico de numerologia
y visiones cientificas como la fisica quantica los hipercubos los Stargates
como los escritores supieron todo esto es un misterio al igual que los on las piramides,ect.
los templos antiguos tanto el tabernaculo como el de salomon eran cubicos
el tabernaculo era un cubo (el patio exterior) entonces el edificio era 3 cubos (1 el santisimo y 2 el santo)
el santisimo contenia el arca del pacto (otro cuadro)
el de salomon duplico todas las medidas pero el concepto fue el mismo
el templo que vio ezequiel era cubico tenia cuartos dentro de cuartos o un (tesseract)
la nueva jerusalem tambien era cubica con el trono de Jehova ( un cubo dentro de un cubo)en el centro
todo esto resulta fasinante sobre todo cuando la sociedad trata de decir que en medio de todo este SIMBOLISMO
los 144,000 son literales (son virgenes,estan de pie en el monte sion,ect) y que Jehova y Jesus no son el mismo (colosenses 1:15,juan 1:1,hebreos 1:1-4,15, ect)
Si dios hizo la biblia para que la entendieramos ?porque la hizo tan complicada?
a lo mejor este fue su plan para que solo los "iluminados" (nosotros los apostatas) la entendieramos
miren la descripcion del templo de Ezequiel que da la biblia y comparenla con la
figura de la nueva Jerusalen y vean que describen un "hipercubo" el conducto que
Dios usa para viajar de la dimension espiritual a la dimension fisica que vivimos nosotros
el que las escrituras describan estos conceptos es pruba de que tiene que haber habido alguna
intervension extraterrestre ya que no creo que estos simples humanos (Jacob,ezequiel,y Juan)
se hallan podido inventar todo esto por si solo.
Noten la entrada del este y como esta entrada conduce directamente a otro cubo que es
supuestamente el santuario de Dios(su Gloria,su presencia)
noten como El angel entra y saca a ezequiel por todas las puertas del templo y como ilustra el cambio
de dimensiones que el sufre cada vez que entra y sale por una puerta distinta.
todo esto prueba que un ser altamente inteligente (Divino???) estuvo detras de todo esto y que el
proposito de todo esto es que fue escrito para nosotros hoy que podemos entender y vizualisar este
concepto de la dimension espiritual ( el Tercer cielo)

otra imagen del templo de ezequiel
comparenla con el hipercubo
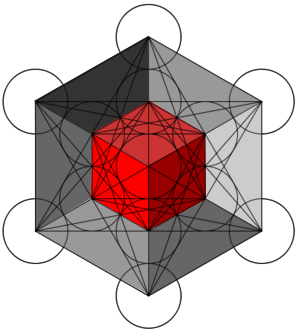
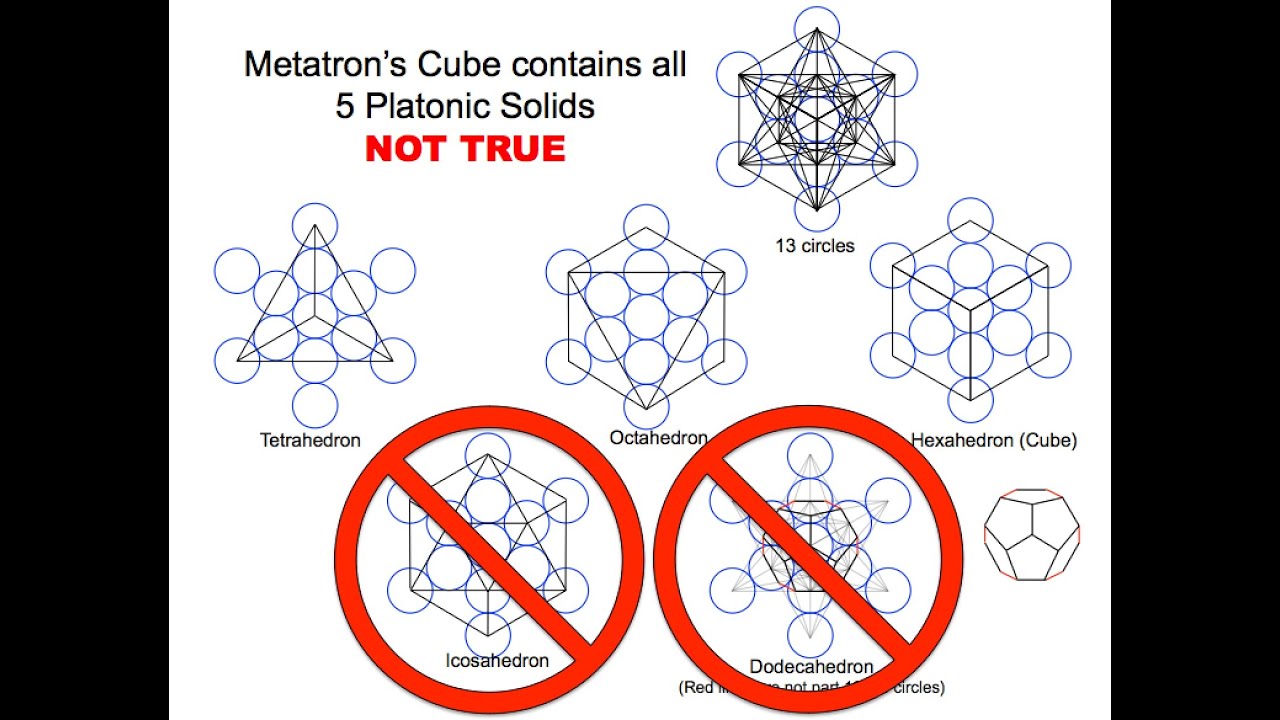
Noten el cubo de metatron y claramente muestra la estrella de David (simbolo del Judaismo) en el centro
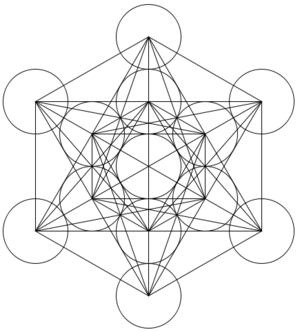
En el judaísmo místico, sobre todo en la Cábala, Metatron (a veces conocido como "Metatrón") es el ángel más alto, más fuerte incluso que Michael. Su nombre significa "más cerca del trono", conocido como el "Príncipe de la Faz Divina", el "Ángel del Pacto", "Rey de los Ángeles" y "Ángel de la Muerte" debido a su gran responsabilidad de estar a cargo de "El apoyo de la existencia del mundo." La etimología de la palabra "Metatron" es muy incierta. Entre las diversas hipótesis que han sido propuestas en este sentido, uno de los más interesantes es que se derivan de los Caldeos "mitra", que significa "lluvia". De la palabra raíz de "turbante", tiene también una cierta relación con la "luz". A propósito, señaló que la doctrina hebrea habla de un "rocío de luz" que emana del "Árbol de la Vida", por el que operar de la resurrección de los muertos, así como una "efusión de rocío" que representa la influencia de los cielos para comunicarse a todos los mundos. Todo esto recuerda el simbolismo alquímico y rosacruz única. Por lo tanto, es posible que la similitud se cree que el dios "Mitra", citado en el hinduismo y el zoroastrismo constituye un préstamo de un extranjero el judaísmo doctrinas. También se puede destacar el papel atribuido a la lluvia en casi todas las tradiciones como un símbolo del descenso de las "influencias espirituales" de los Cielos en la Tierra.
Algunos dicen que Metatrón fue "originado" de Enoc, el padre de Matusalén, un personaje bíblico, que nació en la séptima generación después de Adán. Según el Génesis (capítulo 5, versículos 22-24): "Y Enoc anduvo con Dios, después que engendró a Matusalén, trescientos años, y engendró hijos e hijas. Y todos los días de Enoc trescientos sesenta y cinco años. Y Enoc anduvo con Dios, y él no estaba, porque le llevó Dios. " Este pequeño fragmento sugiere que Dios lo convirtió en Metatron. Acerca de esto hay también personaje bíblico pseudoepigráficos los apócrifos: "Libro de Enoc I" y "Libro de Enoc II", que son parte del canon de algunos grupos religiosos, especialmente los cristianos de Etiopía, pero fueron rechazados por los cristianos y los Judios, a ser especialmente problemático para los clérigos del punto de vista político. Sin embargo, la Epístola de Judas en el Nuevo Testamento de la Biblia, hace una referencia explícita al libro de Enoc, haciendo una breve cita en los versículos 14 y 15 de su capítulo.
Cabe señalar que "Melek", "rey" y "Maleak", "ángel" o "enviados" son en realidad sólo dos formas de la misma palabra de la frase "el ángel en el que Dios" ("ha-Elohim Maleak ") constituye el anagrama de" Mikael ". Hay que añadir que, si Mikael se identifica con Metatrón, como hemos visto, sin embargo, representa sólo un aspecto: la luz. Al lado del lado de la luz, hay un lado oscuro, y esto está representado por Samael, que también se llama "Haolam Sar", es decir, Satanás. De acuerdo a San Hipólito, "el Mesías y el Anticristo son ambos con el emblema del león", que es también un símbolo solar, y la misma observación podría hacerse con la serpiente y muchos otros símbolos.
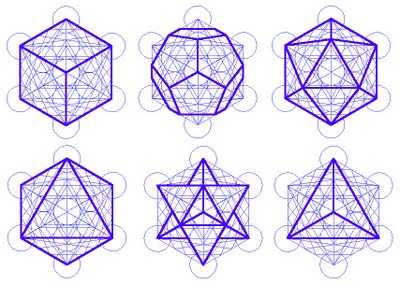
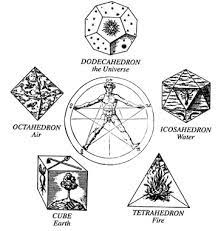
De todos modos, el nombre de "Cubo de Metatrón" es una figura geométrica conocida por lo menos curioso. Esta cifra contiene en sí mismo la proyección bidimensional de todos los cuerpos platónicos. Estos sólidos son, a su vez, poliedro regular convexo, es decir, simétrica de tres figuras geométricas, ángulos y aristas que mantiene un valor constante y cuyos lados son iguales polígonos regulares. Una esfera inscrita, tangente a todas sus caras en su centro, una segunda esfera tangente a todas las aristas en su centro y una esfera circunscrita, pasando por todos los vértices del poliedro. Sólo hay cinco cuerpos platónicos: el tetraedro, hexaedro (o cubo), el octaedro, el dodecaedro y el icosaedro.
|
|
|
|
|
|
NÚMEROS CÚBICOS.
Los números cúbicos son aquellos que obtenemos al elevar al cubo los sucesivos números naturales:
13 = 1; 23 = 8; 33 = 27; .....
Pero también podemos construir estos números geométricamente,
|
|
|

es.walyou.com
2 Alcancia cubo Rubik
521 × 423 - 24k - jpg |

es.wikipedia.org
El interior de un cubo de
232 × 199 - 28k - jpg |

solostocks.com
Cubo Mágico
500 × 500 - 29k - jpg |

pocoseso.com
del Rubik - Cubo Magico -
450 × 338 - 28k - jpg |
Búsquedas relacionadas con cubo magico
EL MISMO "CUBO MAGICO" ES UN HIPERCUBO (HAY UN CUBO MAS CHICO EN EL CENTRO DEL MISMO)
| Reply |
Message 24 of 24 on the subject |
|
El término cuarta dimensión aparece en diversos contextos como la física, las matemáticas y la ciencia ficción. En cada contexto el significado es diferente:
En física, se hace referencia a la cuarta dimensión al hablar del tiempo, principalmente desde el planteamiento de la Teoría de la Relatividad.
En matemática, el concepto aparece asociado o bien a espacios euclídeos de más de tres dimensiones o, más generalmente, a espacios localmente euclídeos o 4-variedades diferenciables.

Hipercubo de 4 dimensiones espaciales girando, tal como se vería proyectado en el espacio tridimensional.
El interés en las dimensiones más altas alcanzó su clímax entre 1870 y 1920.1 En esos años se convirtió en tema frecuente en la literatura fantástica, el arte e incluso algunas teorías científicas. La cuarta dimensión, entendida como dimensión espacial adicional (no como dimensión temporal, como en la teoría de la relatividad) apareció en las obras literarias de Oscar Wilde, Fiódor Dostoyevski, Marcel Proust, H. G. Wells y Joseph Conrad, inspiró algunas obras musicales de Alexander Scriabin, Edgar Varèse y George Antheil y algunas obras plásticas de Pablo Picasso y Marcel Duchamp influyendo en el desarrollo del cubismo. Incluso personajes tan diversos como el psicólogo William James, la escritora Gertrude Stein o el socialista revolucionario Vladimir Lenin se interesaron en el tema.
Igualmente los matemáticos habían estado interesados en el tema al tratar de generalizar los conceptos de la geometría euclídea tridimensional. El matemático Charles L. Dodgson, que enseñó en la Universidad de Oxford, deleitó a generaciones de escolares escribiendo libros, bajo el pseudónimo de Lewis Carroll, que incorporaban algunas ideas sobre la cuarta dimensión. Desde el punto de vista académico, el estudio general de la geometría de la cuarta dimensión en gran parte resultado de los trabajos de Bernhard Riemann. Charles Howard Hinton, matemático y escritor de ciencia ficción británico, acuñó muchos neologismos para describir elementos en la cuarta dimensión. De acuerdo con el Oxford English Dictionary, fue el primero en emplear la palabra tesseract en su libro Una nueva era del pensamiento. También inventó las palabras “kata” (del griego “abajo”) y “ana” (del griego “arriba”) para describir las dos direcciones opuestas en la cuarta dimensión, equivalentes a derecha-izquierda, arriba-abajo, y adelante-atrás.
Los trabajos matemáticos sobre geometrías multidimensionales y geometrías no euclídeas habían sido considerado por los físicos como simples abstracciones matemáticas hasta que Henri Poincaré probó que el grupo de transformaciones de Lorentz que dejaban invariantes las ecuaciones del electromagnetismo podían ser interpretadas como "rotaciones" en un espacio de cuatro dimensiones. Más tarde, los trabajos de Einstein y la interpretación geométrica de estos por parte de Hermann Minkowski llevaron a la aceptación de la cuarta dimensión como una descripción necesaria para explicar los hechos observados relacionados con el electromagnetismo. Sin embargo, aquí la "cuarta dimensión" no era un lugar separado del espacio tridimensional (como en varias de las obras de ficción de la época) ni tampoco una dimensión espacial análoga a las otras tres dimensiones espaciales, sino una dimensión temporal que sólo puede recorrerse hacia el futuro. En la teoría general de la relatividad el campo gravitatorio es explicado como un efecto geométrico de la curvatura de un espacio-tiempo de cuatro dimensiones.
Más tarde, la teoría de Kaluza-Klein propuso que no sólo el campo gravitatorio podía ser interpretado de forma más sencilla como curvatura de un "espacio" de más de tres dimensiones, sino que si se introducía una nueva dimensión espacial enrollada o «compactificada», también el campo electromagnético podía ser interpretado como un efecto geométrico de la curvatura de dimensiones superiores. Así, la Kaluza proponía una teoría de campo unificado del electromagnetismo y la gravedad en un espacio-tiempo de cinco dimensiones, con una dimensión temporal, tres dimensiones espaciales extendidas y una dimensión espacial «compactificada» adicional, que, debido a su condición de compactificada, no era directamente visible pero su efecto era perceptible en forma de campo electromagnético.

Un ángulo recto se describe como un cuarto de una revolución. La Geometría Cartesiana escoge direcciones ortogonales arbitrariamente a través del espacio, lo que significa que cada dirección está en ángulo recto con las demás. Las 3 dimensiones ortogonales del espacio se conocen como altitud, longitud y latitud. La Cuarta Dimensión por lo tanto es la dirección en el espacio con ángulo recto a las 3 direcciones observables.
Un vector espacial es un conjunto de vectores, los cuales podemos imaginarlos como flechas, que proviene de un simple lugar llamado origen (vectores geométricos), que apuntan a otros lugares.
Un punto es un objeto de cero dimensiones. No tiene extensión en el espacio ni propiedades, como una flecha pero sin longitud. Este vector es llamado el vector cero y es el más simple vector espacial.
Una línea es un objeto unidimensional. Si escogemos un cierto vector distinto a cero en una cierta dirección, este vector tiene cierta longitud definida. Ese vector tiene una cabeza en un cierto punto en espacio y una cola en el origen. Si pensamos en estirar que ese vector así sea dos veces su largo, tres veces, etcétera y uniformemente, tomando todas las longitudes posibles (incluso la longitud cero, conseguir el vector cero), conseguiremos una sola línea con una sola dimensión: La de la longitud. Todos los vectores que describen puntos en esta línea serían paralelos. Aunque para visualizar la línea es necesario que ésta tenga un ancho mínimo, sin embargo, una línea de 1D no la tendría.
Un plano es un objeto de dos dimensiones. Tiene longitud y anchura pero no profundidad - algo como una hoja de papel, o más exactamente algo como las imágenes en un televisor común. El pensamiento en un plano en términos de vectores puede ser un poco más desafiante. Si pensamos en tomar un vector y lo movemos de modo que su cola esté tocando la cabeza del primero y esté formando un vector con su cola en el origen y la cabeza en la cabeza del segundo vector colocado de nuevo, tenemos una manera razonable de hablar de vectores de adición. Si tenemos dos vectores que no sean paralelos, podemos hablar de todos los puntos que podemos alcanzar por o solamente el estirar o ningunos de los vectores, y, agregando estos vectores juntos, estos puntos forman un plano.
El espacio, como lo percibimos, es tridimensional. Podemos pensar en poner una línea junto con un plano. Estas líneas son como un emparedado. Para conseguir a un cierto punto en espacio, podemos imaginarnos el viajar encima de la línea y después el movernos a través del plano al punto. Entonces tenemos tres vectores a pensar alrededor, uno a viajar una cierta distancia encima de la línea y dos para conseguir a un cierto punto en espacio.
Para tres rectas ortogonales en el espacio tridimensional (x, y y z) existe una cuarta, normal al espacio, ortogonal a estas tres rectas, que forma un eje p. ej. w.
El producto vectorial es la determinante de una matriz 4×4, donde una de las filas (o columnas) son los vectores unitarios h, i, j y k y las demás (filas o columnas respectivamente) están formadas por las componentes de tres vectores cuadradimensionales cualesquiera, este producto nos dará un cuarto vector perpendicular a estos tres mismos.
La Geometría euclidiana prevé una mayor variedad de formas para existir que en tres dimensiones. Los poliedros tridimensionales son recintos espaciales hechos de caras de dos dimensiones conectadas, los policronos cuadridimensionales son recintos del espacio cuadridimensional hechos de poliedros tridimensionales. Donde en tres dimensiones, hay exactamente cinco poliedros regulares, o los sólidos platónicos, que pueden existir, seis policronos regulares existen en la cuarta dimensión. Cinco de los seis se pueden interpretar como extensiones naturales de los sólidos platónicos, así como el cubo, un sólido platónico, es una extensión del cuadrado de dos dimensiones. El pentachoron está hecho de 5 tetraedros para las caras y 10 caras triangulares, y es el análogo cuadridimensional del tetraedro. El teseracto, o el hipercubo, se compone de 8 caras cúbicas y de 24 cuadrados, y es el politopo cuadridimensional medido. Los teseractos se doblan, la 16-celdas, son el equivalente del octaedro, pues son ambos politopos de cruz. Los politopos de 120 celdas y los de 600 celdas se doblan de igual modo, y son análogos al dodecaedro y al icosaedro, respectivamente. El de 24 celdas es un policrono regular único y que no tiene ningún equivalente tridimensional. Apenas pues la esfera, o 2-esfera, es una superficie de dos dimensiones curvada compuesta de todos los puntos equidistantes de un punto central dado, en un espacio tridimensional, la 3-esfera, una clase de hiperesfera, es el espacio que contiene todos los puntos equidistantes a un punto central dado, en un espacio cuadridimensional. Cada sección transversal tridimensional de un 3-esfera es un 2-esfera.

La analogía dimensional se usa frecuentemente para comprender el salto de una dimensión (en este caso, la tercera dimensión) a una más alta (cuarta dimensión). La analogía dimensional consiste en resolver un problema en n + 1 dimensiones relacionándolo primero con un problema análogo de (n - 1) dimensión, vale decir, "una dimensión menos". E igualmente debe analizarse el caso de cómo se relaciona el problema en n con el de (n + 1) dimensiones, es decir, "una más".
Edwin Abbott Abbott en su libro Planilandia (Flatland) escribe sobre un "ser cuadrado" que vive en un mundo de dos dimensiones, como la superficie de un pedazo de papel. Este "cuadrado" se enfrenta a experimentos de un ser tridimensional. El ser tridimensional es percibido por el "cuadrado" como un ser aparentemente divino, ya que puede poner y quitar objetos de una caja fuerte sin romperla ni abrirla (moviéndolos a través de su tercera dimensión), ver todo desde de la perspectiva de dos dimensiones sea incluido detrás de las paredes (puesto que ve "sobre" Planilandia), y totalmente invisible para los habitantes de Planilandia, puesto que está "arriba" y una dimensión por arriba de las dos dimensiones en las que el cuadrado está atrapado. No obstante, el ser tridimensional podría manifestarse en el mundo de dos dimensiones, pero sólo parcialmente, si fuera una esfera, aparecería como una secuencia de círculos sucesivos "que cambian de tamaño" (intersecciones de la esfera con el plano de dos dimensiones). Aplicando analogía dimensional, uno puede deducir que el ser cuadridimensional sería capaz de hazañas similares de nuestra perspectiva tridimensional.
Rudy Rucker demuestra esto en su novela "Spaceland", en la cual el protagonista encuentra los seres cuadridimensionales que demuestran tales energías. Un uso útil de la analogía dimensional en visualizar la cuarta dimensión está en la proyección. Una proyección es una manera para representar un objeto (n+1)-dimensional en la n-dimensión. Por ejemplo, las pantallas de computadora son de dos dimensiones, y todas las fotografías de objetos tridimensionales son representadas en dos dimensiones puesto que la información de la tercera dimensión (o de la profundidad) no puede ser representada por la pantalla (si el observador se mueve, aleje o acerque, la imagen no cambiará). En este caso, la profundidad se quita y se substituye por la información indirecta. La retina del ojo es un arsenal de dos dimensiones de receptores pero puede permitir que el cerebro perciba la naturaleza de objetos tridimensionales usando la información indirecta (como la perspectiva, el sombreado, visión binocular, etc.).
La perspectiva del uso de los artistas da profundidad tridimensional a los cuadros de dos dimensiones. Asimismo, los objetos en la cuarta dimensión se pueden proyectar matemáticamente a las familiares tres dimensiones, donde pueden entonces ser examinados más convenientemente. En este caso, la "retina de un ojo cuadridimensional" tendría un arsenal de receptores tridimensionales. El ser hipotético con tal ojo percibiría la naturaleza de objetos cuadridimensionales usando la información indirecta contenida en las imágenes que recibe en su retina. La proyección de la perspectiva a partir de cuatro dimensiones produce efectos similares como en el caso tridimensional, tal como la perspectiva.
Esto agrega "profundidad cuadridimensional" a estos cuadros tridimensionales. La analogía dimensional también ayuda a entender tales proyecciones. Por ejemplo, los objetos de dos dimensiones son limitados por límites unidimensionales: un cuadrado es limitado por cuatro bordes o líneas. Los objetos tridimensionales son limitados por superficies de bidimensionales: un cubo es limitado por 6 cuadrados. Aplicando analogía dimensional, uno puede deducir que un cubo cuadridimensional, conocido como teseracto, es limitado por los volúmenes tridimensionales.
Y de hecho, éste es el caso matemáticamente: el teseracto es limitado por 8 cubos. Saber esto es indispensable para entender cómo interpretar una proyección tridimensional del teseracto. Los límites del teseracto proyectan a los volúmenes en la imagen, superficies no simplemente de dos dimensiones. Esto ayuda a entender las características de dichas dimensiones que de otra manera sólo confundirían. De igual manera, el concepto de sombras puede ayudarnos mejor a entender la teoría de cuatro dimensiones. Si usted proyectara una luz sobre objeto tridimensional, éste proyectaría una sombra de dos dimensiones. Por lo tanto la luz en un objeto de dos dimensiones echaría una sombra unidimensional (en un mundo de dos dimensiones), y la luz en un objeto unidimensional en un mundo unidimensional echaría una sombra cero-dimensional, es decir, un punto de la no-luz. Esta idea se puede utilizar en la otra dirección; la luz en un objeto cuadridimensional proyectaría una sombra tridimensional. Como ejemplo, la sombra de un cubo transparente, proyectaría una sombra sobre el papel, de dos cuadrados, unidos por sus vértices con 4 segmentos.
Semejantemente, si era un cubo cuadridimensional iluminado con luz de 4 dimensiones, su sombra sería la de un cubo tridimensional dentro de otro cubo tridimensional. Siendo tridimensionales podemos solamente ver el mundo con nuestros ojos en dos dimensiones; el ser cuadridimensional consideraría el mundo en tres. Así podría, por ejemplo, ver los seis lados de una caja opaca simultáneamente. No solamente eso; también podría ver lo que hay al interior de la caja, como en Planilandia, en donde la esfera ve objetos en el mundo de dos dimensiones y todo dentro de ellos simultáneamente. Análogo, un espectador cuadridimensional vería todos los puntos en nuestro espacio tridimensional simultáneamente, incluyendo la estructura interna de objetos sólidos y de cosas obscurecidos de nuestro punto de vista.
Albert Einstein en su célebre teoría de 1905 de la relatividad especial habló por primera vez del tiempo como una cuarta dimensión y como algo indispensable para ubicar un objeto en el espacio y en un momento determinado. El tiempo en la teoría de la relatividad no es una dimensión espacial más, ya que fijado un punto del espacio-tiempo éste puede ser no alcanzable desde nuestra posición actual, hecho que difiere de la concepción usual de dimensión espacial. Aunque inicialmente se interpretó el tiempo como una "dimensión" matemática necesaria para ubicar un evento u objeto, en la teoría de la relatividad general el tiempo es tratado como una dimensión geométrica más, aunque los objetos materiales no puedan seguir una trayectoria completamente arbitraria a lo largo del tiempo (como por ejemplo "dar la vuelta" y viajar al pasado). La necesidad del tiempo dentro de la teoría de la relatividad es necesaria por dos motivos:
En primer lugar, los objetos no sólo se mueven a través del espacio sino que también lo hacen a través del tiempo, es decir su coordenada temporal aumenta continuamente, por lo que hubo la necesidad de hablar del tiempo ligado al espacio como la cuarta dimensión (en inglés spacetime, en castellano espacio-tiempo). Además el ritmo de avance en la dimensión temporal depende del estado de movimiento del observador, produciéndose una dilatación temporal efectiva para los observadores más rápidos en relación al tiempo medido por un observador estacionario.
En segundo lugar, el carácter intrínseco del espacio-tiempo y su cuatridimensionalidad requiere un modo conceptualmente diferente de tratar la geometría del universo, puesto que una cuarta dimensión implica un espacio plano (bidimensional) que se curva en la teoría de la relatividad general por la acción de la gravedad de la materia originándose la curvatura del espacio-tiempo.
Finalmente cabe añadir que algunas teorías físicas como la teoría de Kaluza-Klein y las teoría de supercuerdas, en sus varias versiones, añaden a las tres dimensiones físicas espaciales entre 1 y 9 dimensiones espaciales adicionales, de tipo compacto; además de la dimensión temporal.
|
|
|
|
|
|
|
|
|

| Reply |
Message 119 of 121 on the subject |
|
|

The TABERNACLE
|
|
| Reply |
Message 120 of 121 on the subject |
|
|
|
| Reply |
Message 121 of 121 on the subject |
|
|
CONEXION DE LA MANZANA (ESTRELLA DE 5 PUNTAS=NUMERO PHI= 1.618033..) CON EL RELOJ (GEMATRIA DE PHI EN INGLES ES 33)

klockit.com
6" Star of David Theme Clock
750 × 735 - 65k - jpg |

amazon.com
STAR OF DAVID Wall Clock
355 × 355 - 34k - jpg |

cafepress.com
Star of David Wall Clock
225 × 225 - 12k - jpg |

amazon.com
Wall Clock Blue Star of David
1000 × 1000 - 84k - jpg |
|
|
|
54. Job 33:33 Y si no, óyeme tú a mí;
Calla, y te enseñaré sabiduría.
666= SISTEMA SEXAGECIMAL= RELOJ
|
| Reply |
Message 3 of 3 on the subject |
|
|
54. Job 33:33 Y si no, óyeme tú a mí;
Calla, y te enseñaré sabiduría.
666= SISTEMA SEXAGECIMAL= RELOJ
|
|
|
|
|
|
|
|
|
|
|
W/WEST/UBICACION DEL LUGAR SANTISIMO
W=LETRA NUMERO 23 EN EL ALFABETO INGLES
W/LOBO/WOLF /PERRO / BENJAMIN
SIRIO/ BENJAMIN
Job
25:1 Respondió Bildad suhita, y dijo:
25:2 El señorío y el temor están con él; El hace paz en sus alturas.
25:3 ¿Tienen sus ejércitos número? ¿Sobre quién no está su luz?
25:4 ¿Cómo, pues, se justificará el hombre para con Dios? ¿Y cómo será limpio el que nace de mujer?
25:5 He aquí que ni aun la misma luna será resplandeciente, Ni las estrellas son limpias delante de sus ojos;
25:6 ¿Cuánto menos el hombre, que es un gusano, Y el hijo de hombre, también gusano?
WORMHOLE / LETRA W / (AGUJERO DE GUSANO)
agujero blanco=hombre=boaz
agujero negro=mujer=jachin
salmo 119 (alfa y el omega)
entre los mismos hay un obvio "agujero de gusano"
el hijo, es el OBVIO "AGUJERO DE GUSANO"
| Reply |
Message 281 of 281 on the subject |
|
|
|
|
|
|
 First First  Previous 2 to 2 of 2 Next Previous 2 to 2 of 2 Next  Last Last  |
|
|
|
|
|
¿COMO EXPLICAS EL NEXO 911 CON EL DIA DE MARIA MAGDALENA EN EL MARCO A LA INDEPENDENCIA DE EEUU EN FILADELFIA?
11/9/2001-11/9/2005=1461 DIAS
11/9/2005-22/7/2006=315 DIAS
1461+315=1776
EL 4/7/1776=INDEPENDENCIA DE EEUU EN FILADELFIA
En aquel tiempo, respondiendo Jesús, dijo:
Te alabo, Padre, Señor del cielo y de la tierra,
que hayas escondido estas cosas (la Gnosis, la Sabiduría Oculta)
de los sabios (de los eruditos) y de los entendidos, (de los intelectuales)
y las hayas revelado á los niños. (A los Iniciados). Así, Padre, pues que así agradó en tus ojos."
(Mateo 11: 25-26).
EL PATRON KAVALISTICO DE LA INDEPENDENCIA DE LOS ESTADOS UNIDOS ESTA TOTALMENTE INTERRELACIONADO CON LAS BODAS DE CANA, EN EL CONTEXTO A QUE LA MISMA NO FUE SOLAMENTE EN UN TERCER DIA ( JUAN 2:1), SINO QUE TAMBIEN EN UN SEPTIMO DIA (JUAN 1:29,35,42 Y JUAN 2:1). DE ALLI SALE EL MONSTRUSO NUMERO 37.
1776=48*37
666=37*18
37*18=666
37*48=1776 (AÑO DE LA INDEPENDENCIA DE EEUU)
LA MISMA TORRE ES UN SIMBOLO FALICO CON FUERTE CONNOTACION SEXUAL
|
|
|
|
|
|
|
22/7=3.14=PI
12 PUNTOS EN SU CIRCUNFERENCIA=RELOJ=SANTA CENA
LONGITUD CIRCUNFERENCIA=PIxDIAMETRO
 |
|
|
|
|
|
|
|
|
|
|







 



|

LLAVE DE ORO Y DE PLATA AL IGUAL QUE LA MANZANA
Incendio Notre Dame: Última hora de la catedral de París (15 DE ABRIL)

 Incendio Notre Dame (París), en directo (Bertrand Guay / AFP)
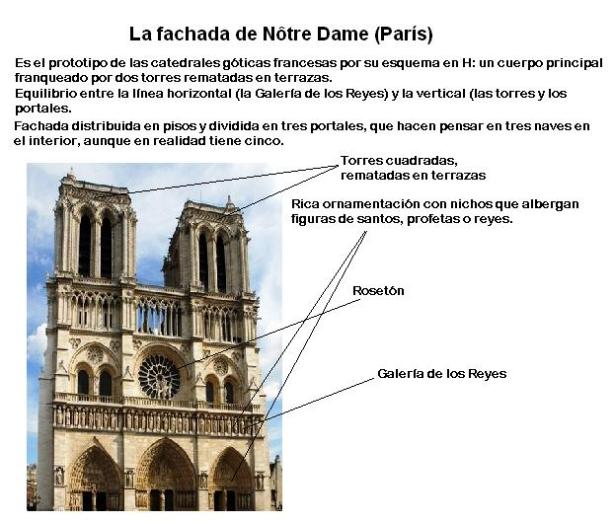
PHI A NOTRE-DAME
A la catredal de Notre Dame hi observem més rectanlges auris: Creat per Mario Pastor 
The DaVinci Code, Notre Dame Cathedral from DaVinci Code
original movie prop
HEXAGONO=OCTAHEDRO =ESTRELLA DE 6 PUNTAS= SATURNO =CUBO/HEXAGONO= ESPACIO/TIEMPO =1 DE REYES 6:20 Y APOCALIPSIS 21:16
EL SEXTO DIA ES EL VIERNES Y EL OCTAVO EL DOMINGO. INCREIBLE
   

August 23, 2018/

The Golden Section (aka Golden Mean, and Golden Ratio) phys.org
We use math in architecture on a daily basis to solve problems. We use it to achieve both functional and aesthetic advantages. By applying math to our architectural designs through the use of the Golden Section and other mathematical principles, we can achieve harmony and balance. As you will see from some of the examples below, the application of mathematical principles can result in beautiful and long-lasting architecture which has passed the test of time.
Using Math in Architecture for Function and Form
We use math in architecture every day at our office. For example, we use math to calculate the area of a building site or office space. Math helps us to determine the volume of gravel or soil that is needed to fill a hole. We rely on math when designing safe building structures and bridges by calculating loads and spans. Math also helps us to determine the best material to use for a structure, such as wood, concrete, or steel.
“Without mathematics there is no art.” – Luca Pacioli, De divina proportione, 1509
Architects also use math when making aesthetic decisions. For instance, we use numbers to achieve attractive proportion and harmony. This may seem counter-intuitive, but architects routinely apply a combination of math, science, and art to create attractive and functional structures. One example of this is when we use math to achieve harmony and proportion by applying a well-known principle called the Golden Section
Math and Proportion – The Golden Section

Perfect proportions of the human body – The Vitruvian Man – by Leonardo da Vinci.
We tend to think of beauty as purely subjective, but that is not necessarily the case. There is a relationship between math and beauty. By applying math to our architectural designs through the use of the Golden Section and other mathematical principles, we can achieve harmony and balance.
The Golden Section is one example of a mathematical principle that is believed to result in pleasing proportions. It was mentioned in the works of the Greek mathematician Euclid, the father of geometry. Since the 4th century, artists and architects have applied the Golden Section to their work.
The Golden Section is a rectangular form that, when cut in half or doubled, results in the same proportion as the original form. The proportions are 1: the square root of 2 (1.414) It is one of many mathematical principles that architects use to bring beautiful proportion to their designs.
Examples of the Golden Section are found extensively in nature, including the human body. The influential author Vitruvius asserted that the best designs are based on the perfect proportions of the human body.
Over the years many well-known artists and architects, such as Leonardo da Vinci and Michelangelo, used the Golden Section to define the dimensions and proportions in their works. For example, you can see the Golden Section demonstrated in DaVinci’s painting Mona Lisa and his drawing Vitruvian Man.
Famous Buildings Influenced by Mathematical Principles
Here are some examples of famous buildings universally recognized for their beauty. We believe their architects used math and the principals of the Golden Section in their design:
Parthenon
The classical Doric columned Parthenon was built on the Acropolis between 447 and 432 BC. It was designed by the architects Iktinos and Kallikrates. The temple had two rooms to shelter a gold and ivory statue of the goddess Athena and her treasure. Visitors to the Parthenon viewed the statue and temple from the outside. The refined exterior is recognized for its proportional harmony which has influenced generations of designers. The pediment and frieze were decorated with sculpted scenes of Athena, the Gods, and heroes.

Parthenon Golden Section
Notre Dame Cathedral in Paris
Built on the Ile de la Cite, Notre Dame was built on the site of two earlier churches. The foundation stone was laid by Pope Alexander III in 1163. The stone building demonstrates various styles of architecture, due to the fact that construction occurred for over 300 years. It is predominantly French Gothic, but also has elements of Renaissance and Naturalism. The cathedral interior is 427 feet x 157 feet in plan. The two Gothic towers on the west façade are 223 feet high. They were intended to be crowned by spires, but the spires were never built. The cathedral is especially loved for its three stained glass rose windows and daring flying buttresses. During the Revolution, the building was extensively damaged and was saved from demolition by the emperor Napoleon.

Notre Dame Cathedral in Paris
Taj Mahal
Built in Agra between 1631 and 1648, the Taj Mahal is a white marble mausoleum designed by Ustad-Ahmad Lahori. This jewel of Indian architecture was built by Emperor Shah Jahan in memory of his favorite wife. Additional buildings and elements were completed in 1653. The square tomb is raised and is dramatically located at the end of a formal garden. On the interior, the tomb chamber is octagonal and is surrounded by hallways and four corner rooms. Building materials are brick and lime veneered with marble and sandstone.

Taj Mahal designed by Ustad-Ahmad Lahori
As you can see from the above examples, the application of mathematical principles can result in some pretty amazing architecture. The architects’ work reflects eye-catching harmony and balance. Although these buildings are all quite old, their designs have pleasing proportions which have truly passed the test of time.
https://bleckarchitects.com/math-in-architecture/
|
|
|
|
|
|
|


https://es.wikipedia.org/wiki/Albert_Einstein
Albert Einstein (en alemán [ˈalbɛɐ̯t ˈaɪnʃtaɪn]; Ulm, Imperio alemán, 14 de marzo de ... En 1915 presentó la teoría de la relatividad general, en la que reformuló por completo el concepto de gravedad. ...... Einstein, Albert (1905e) [manuscrito recibido 27 de septiembre 1905], «Ist die Trägheit eines Körpers von seinem ...
rpp.pe › Lima
27 sep. 2015 - ... primera vez su Teoría de la Relatividad Especial, también llamada restringida; y en 1960, muere el ... 27 de septiembre del 2015 - 12:01 AM ...
ar.tuhistory.com/etiquetas/teoria-de-la-relatividad
Albert Einstein publica la teoría general de la relatividad ... De la teoría especial de la relatividad se deduce su famosa ecuación E=mc2, ... 27-09-1905 D.C..
https://www.gabitos.com/DESENMASCARANDO_LAS_FALSAS.../template.php?...
7 ene. 2014 - En 1905 Einstein publicó su teoría de la relatividad especial, que ...... Einstein presentó a los editores de Annalen el 27 de septiembre del ...
MATT 16:18 is an in your face glyph for the golden mean ratio 1.618
(“MATT” is pun of “MATTER”)
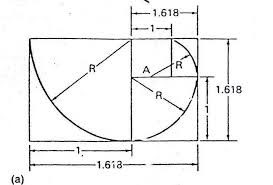
Golden Mean ratio of 1.618

The Golden Mean and the Equilateral Triangle in a Circle; THE CRUCIAL FACT IS THE MIDPOINT OF THE TRIANGLE SIDE
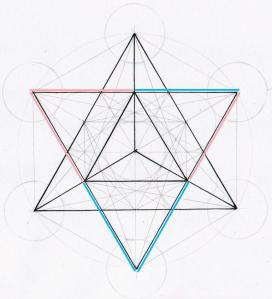
Star Tetrahedron, formed by the MIDPOINTS OF THE CENTRAL EQUILATERAL TRIANGLE (the blue and rose colored lines indicate these midpoint halves)
Saint Mary Magdalene in Venice
 A closer look 
 the Apple
|
|
|
|
|


Desde que Leonardo concluyó su célebre pintura en el siglo XV, se han tejido numerosos mitos y leyendas alrededor de esta obra de arte, considerada por los críticos como su “obra más serena y alejada del mundo temporal” y diseñada para poder ser observada en su totalidad y tener una sensación de inmersión. De partida, llama la atención la configuración de sus protagonistas: Jesús ocupa el centro de la escena, y a sus lados existe un equilibrio con seis discípulos a cada lado, agrupados de tres en tres. Los discípulos, según algunos estudiosos, estarían agrupados en “rectángulos”, cuyo significado es unidad y estabilidad. En el centro está Jesús y, al contrario que todos los demás, se encuentra circunscrito en un “triángulo equilátero”, que significa equilibrio perfecto, el triángulo donde reside la majestad y el poder de Dios. El número tres, por lo demás, representa al hombre (cuerpo, mente y espíritu) y a la deidad (Padre, Hijo y Espíritu Santo).

Al fondo del cuadro se puede observar tres ventanales que iluminan la parte central donde está Jesús y donde puede entreverse un paisaje que para algunos simbolizaría el Paraíso (algunos estudios recientes dicen que este paisaje podría corresponder a la zona norte del lago Como, en Italia). Además, con respecto a Judas Iscariote, se comenta que el modelo que Leonardo utilizó fue un verdadero criminal, pues da Vinci habría visitado distintas cárceles de Milán para tales efectos. Algunos también han postulado que el propio Leonardo Da Vinci se pintó a sí mismo en el rol del apóstol Judas Tadeo (un gran predicador que evangelizó a muchos pueblos y que fue el portador de la Sábana Santa después de la muerte de Cristo), aunque hay que consignar que la pintura data de 1495-1497, y en ese tiempo Leonardo tenía 45 años, mientras que el aspecto del apóstol, la penúltima figura de izquierda a derecha, es de mucha más edad.
 
La figura de Judas Tadeo, que en el extremo derecho del cuadro aparece conversando con el mismo Simón el Zelote, estaría basada por su parte en el filósofo Platón, un sabio que debido a sus planteamientos con respecto a la divinidad no era muy querido por la iglesia. Judas Tadeo y Simón el Zelote – o Da Vinci y Platón para algunos- a primera vista aparecen en “La última cena” manteniendo un tranquilo diálogo, ajenos a lo que sucede en la mesa, al revuelo creado, como si ellos estuvieran hablando de cosas más trascendentales e importantes.
         |
|
|
 Primer Primer
 Anterior
22 a 36 de 36
Següent Anterior
22 a 36 de 36
Següent
 Darrer
Darrer

|
|
| |
|
|
©2024 - Gabitos - Tots els drets reservats | |
|
|

