|
جواب |
رسائل 1 من 30 في الفقرة |
|
|
|
|
|
جواب |
رسائل 16 من 30 في الفقرة |
|
|
|
|
جواب |
رسائل 17 من 30 في الفقرة |
|
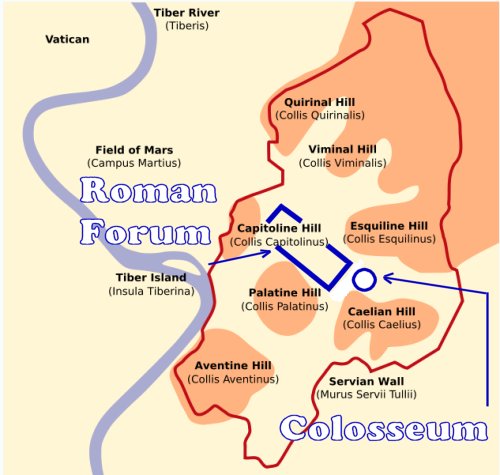
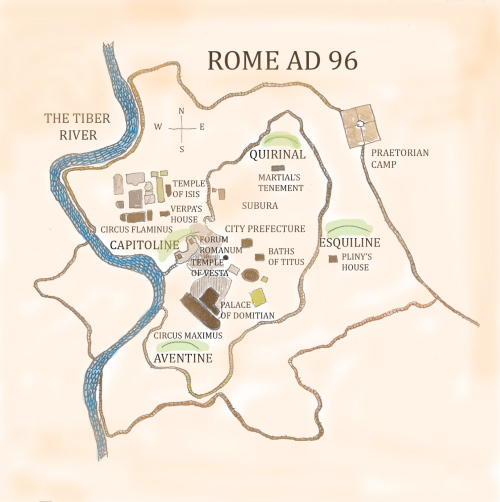
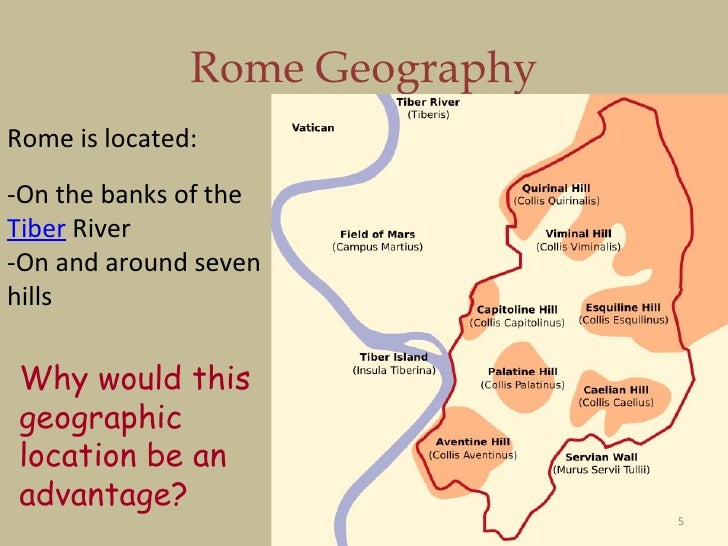
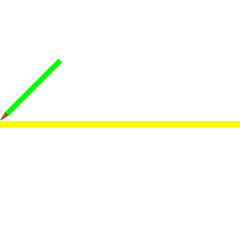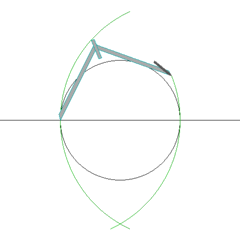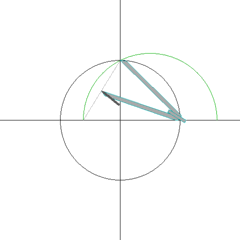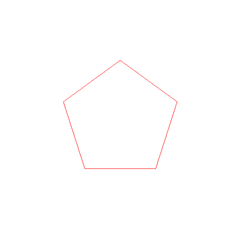
PARA NO CREER PERO ESTO ES ASI. LA RELACION DEL DINERO / MONEY / MOON / CON LA LUNA EN EL CONTEXTO A LA TRANSFIGURACION EN EL MONTE HERMON / MON / LUNA EN LA TRIBU DE DAN / DINERO / SERPIENTE. TODO ES UN NEXO CON LA TRANSFIGURACION DEL SEÑOR. DINERO ES TIEMPO MISMO.
ES OBVIO EL NEXO DE LA SERPIENTE CON LA MUJER
NOTEN EL NEXO DE DAN, CON LA SERPIENTE (VENECIA) Y EL CABALLO (PLAZA SAN MARCOS)
7. Génesis 49:17 Será Dan SERPIENTE junto al camino, Víbora junto a la senda, Que muerde los talones del caballo, Y hace caer hacia atrás al jinete.
 1200 1200
|
|
|
|
جواب |
رسائل 18 من 30 في الفقرة |
|
|
|
|
جواب |
رسائل 19 من 30 في الفقرة |
|
Fibonacci 24 Repeating Pattern
May 15, 2012 by Gary Meisner
The Fibonacci sequence has a pattern that repeats every 24 numbers.
Numeric reduction is a technique used in analysis of numbers in which all the digits of a number are added together until only one digit remains. As an example, the numeric reduction of 256 is 4 because 2+5+6=13 and 1+3=4.
Applying numeric reduction to the Fibonacci series produces an infinite series of 24 repeating digits:
1, 1, 2, 3, 5, 8, 4, 3, 7, 1, 8, 9, 8, 8, 7, 6, 4, 1, 5, 6, 2, 8, 1, 9
If you take the first 12 digits and add them to the second twelve digits and apply numeric reduction to the result, you find that they all have a value of 9.
| 1st 12 numbers |
1 |
1 |
2 |
3 |
5 |
8 |
4 |
3 |
7 |
1 |
8 |
9 |
| 2nd 12 numbers |
8 |
8 |
7 |
6 |
4 |
1 |
5 |
6 |
2 |
8 |
1 |
9 |
| Numeric reduction – Add rows 1 and 2 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
18 |
| Final numeric reduction – Add digits of result |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
This pattern was contributed both by Joseph Turbeville and then again by a mathematician by the name of Jain.
We would expect a pattern to exist in the Fibonacci series since each number in the series encodes the sum of the previous two. What’s not quite so obvious is why this pattern should repeat every 24 numbers or why the first and last half of the series should all add to 9.
For those of you from the “Show Me” state, this pattern of 24 digits is demonstrated in the numeric reduction of the first 73 numbers of the Fibonacci series, as shown below:
|
Fibonacci Number
|
Numeric reduction by adding digits |
| 1st Level |
2nd Level |
Final Level |
| Example: 2,584 |
2+5+8+4=19 |
1+9=10 |
1+0=1 |
| 0 |
0 |
0 |
0 |
| 1 |
1 |
1 |
1 |
| 1 |
1 |
1 |
1 |
| 2 |
2 |
2 |
2 |
| 3 |
3 |
3 |
3 |
| 5 |
5 |
5 |
5 |
| 8 |
8 |
8 |
8 |
| 13 |
4 |
4 |
4 |
| 21 |
3 |
3 |
3 |
| 34 |
7 |
7 |
7 |
| 55 |
10 |
1 |
1 |
| 89 |
17 |
8 |
8 |
| 144 |
9 |
9 |
9 |
| 233 |
8 |
8 |
8 |
| 377 |
17 |
8 |
8 |
| 610 |
7 |
7 |
7 |
| 987 |
24 |
6 |
6 |
| 1,597 |
22 |
4 |
4 |
| 2,584 |
19 |
10 |
1 |
| 4,181 |
14 |
5 |
5 |
| 6,765 |
24 |
6 |
6 |
| 10,946 |
20 |
2 |
2 |
| 17,711 |
17 |
8 |
8 |
| 28,657 |
28 |
10 |
1 |
| 46,368 |
27 |
9 |
9 |
| 75,025 |
19 |
10 |
1 |
| 121,393 |
19 |
10 |
1 |
| 196,418 |
29 |
11 |
2 |
| 317,811 |
21 |
3 |
3 |
| 514,229 |
23 |
5 |
5 |
| 832,040 |
17 |
8 |
8 |
| 1,346,269 |
31 |
4 |
4 |
| 2,178,309 |
30 |
3 |
3 |
| 3,524,578 |
34 |
7 |
7 |
| 5,702,887 |
37 |
10 |
1 |
| 9,227,465 |
35 |
8 |
8 |
| 14,930,352 |
27 |
9 |
9 |
| 24,157,817 |
35 |
8 |
8 |
| 39,088,169 |
44 |
8 |
8 |
| 63,245,986 |
43 |
7 |
7 |
| 102,334,155 |
24 |
6 |
6 |
| 165,580,141 |
31 |
4 |
4 |
| 267,914,296 |
46 |
10 |
1 |
| 433,494,437 |
41 |
5 |
5 |
| 701,408,733 |
33 |
6 |
6 |
| 1,134,903,170 |
29 |
11 |
2 |
| 1,836,311,903 |
35 |
8 |
8 |
| 2,971,215,073 |
37 |
10 |
1 |
| 4,807,526,976 |
54 |
9 |
9 |
| 7,778,742,049 |
55 |
10 |
1 |
| 12,586,269,025 |
46 |
10 |
1 |
| 20,365,011,074 |
29 |
11 |
2 |
| 32,951,280,099 |
48 |
12 |
3 |
| 53,316,291,173 |
41 |
5 |
5 |
| 86,267,571,272 |
53 |
8 |
8 |
| 139,583,862,445 |
58 |
13 |
4 |
| 225,851,433,717 |
48 |
12 |
3 |
| 365,435,296,162 |
52 |
7 |
7 |
| 591,286,729,879 |
73 |
10 |
1 |
| 956,722,026,041 |
44 |
8 |
8 |
| 1,548,008,755,920 |
54 |
9 |
9 |
| 2,504,730,781,961 |
53 |
8 |
8 |
| 4,052,739,537,881 |
62 |
8 |
8 |
| 6,557,470,319,842 |
61 |
7 |
7 |
| 10,610,209,857,723 |
51 |
6 |
6 |
| 17,167,680,177,565 |
67 |
13 |
4 |
| 27,777,890,035,288 |
73 |
10 |
1 |
| 44,945,570,212,853 |
59 |
14 |
5 |
| 72,723,460,248,141 |
51 |
6 |
6 |
| 117,669,030,460,994 |
65 |
11 |
2 |
| 190,392,490,709,135 |
62 |
8 |
8 |
| 308,061,521,170,129 |
46 |
10 |
1 |
| 498,454,011,879,264 |
72 |
9 |
9 |
Thanks to Joseph Turbeville for sending “A Glimmer of Light from the Eye of a Giant” and to Helga Hertsig for bringing Jain’s discovery of this pattern to my attention.
Filed Under: Math
https://www.goldennumber.net/fibonacci-24-pattern/ |
|
|
|
جواب |
رسائل 20 من 30 في الفقرة |
|
|
|
|
جواب |
رسائل 21 من 30 في الفقرة |
|
Fibonacci Fun
Here are some illustrations by myself and others, dealing with the Fibonacci sequence and the Golden Number, Phi.

A few months ago, I noticed the exponents of Phi encode the Fibonacci sequence.


The sequence gets closer to the golden number the larger the numbers get. This will work with any two starting numbers, like say 91 and 432, for example. You’ll find the same ratio emerge if you keep adding them together. (91+432 = 523, then, 432+523=955, etc) Already we are at 1.8 to 1. (955/523) A handful more steps and we’ll have Phi to more than 99.999% accuracy.

???? If you had a million phalanges, your hand would look like King Midas.

Jain108 made a post on how, if you start with 2 and 10, you arrive at the actual numbers found in the exponents of Phi. Remember exponents are simply the number multiplied by itself n number of times. Phi cubed, or Phi to the third power, is just Phi x Phi x Phi. (1.618 x 1.618 x 1.618 = 4.236) See that was easy, now stop complaining how you’re bad at math.

Phi to the negative power is the same as saying, one divided by the Phi cubed, or whatever.

Here’s some different ways to say the same thing.

This does an excellent job of explaining where all these freaking numbers come from. (img Scott Onstott)

Circles of Fibonacci. Magenta and green cancel out and make gold
Sam Kutler found the golden number in concentric circles.

The outer ring shows the 24 digit pattern(digital roots), the inner the 60 digit pattern(last number).
Lucien Khan rediscovered the 60 digit repeat pattern.
Fibonacci Patterns
Fibonacci sequence hidden in ordinary division problem:
If you divide 1 by 999,999,999,999,999,999,999,999,999,999,999,999,999,999,999,999 (that’s 999 quattuordecillion), the Fibonacci sequence pops out.

Chad Adam’s Extended Fibonacci Series

Like I said, you can start a Fibonacci sequence with any two numbers. If you begin with the numbers 1-9, some interesting things happen.

by Chad Adams

See how the numbers match up?

The Platonic Solids

 back to the 60 digit pattern…. back to the 60 digit pattern….

The Fibonacci Sequence, starting at the 60th number in the sequence. See the pattern? Just look at the last digit in each number of the sequence. [after 8 is 3 because the last digit in 13(5+8) is 3]



The Colorado State Flag
Is it just me or is Colorado’s state seal illuminaty as all hell?

Don’t even go to Denver International Airport.

I did an article on Decoding the Dollar, and found the leaves on the left side of the buck encode the fib seq. with 2,3,5,8.


The name ‘Fi-Bonacci'(Man of cheer) comes from Leonardo’s old man who could always make the town laugh.

Leonardo de Pisa, the guy we call ‘Fibonacci”, actually had his own value for π, which was 864/275, or 3.141818181818…. (Phi = 1.618..)


I talk about this more here..

The Fibonacci numbers reduced to one digit through digital parity. (21 is 3 because 2+1=3)
This is the number and sequence of numbers that God choose to use to structure all life and creation.
https://joedubs.com/fibonacci-fun/ |
|
|
|
جواب |
رسائل 22 من 30 في الفقرة |
|
Check this out! The fibonacci sequence; #, Full Value, Decimal Parity Value 1 1 1 2 1 1 3 2 2 4 3 3 5 5 5 6 8 8 7 13 4 8 21 3 9 34 7 10 55 1 11 89 8 12 144 9 13 233 8 14 377 8 15 610 7 16 987 6 17 1597 4 18 2584 1 19 4181 5 20 6765 6 21 10946 2 22 17711 8 23 28657 1 24 46368 9 25 75025 1 26 121393 1 27 196418 2 28 317811 3 29 514229 5 30 832040 8 31 1346269 4 32 2178309 3 33 3524578 7 34 5702887 1 35 9227465 8 36 14930352 9 37 24157817 8 38 39088169 8 39 63245986 7 40 102334155 6 41 165580141 4 42 267914296 1 43 433494437 5 44 701408733 6 45 1134903170 2 46 1836311903 8 47 2971215073 1 48 4807526976 9 It repeats fully in lots of 24 or half in 12! It's more obvious if I re-number the positions by 12's. (btw, 12 is a second generation 3) Just match the positions and observe the symmetry around 9 once more... 1 1 1 2 1 1 3 2 2 4 3 3 5 5 5 6 8 8 7 13 4 8 21 3 9 34 7 10 55 1 11 89 8 12 144 9 1 233 8 2 377 8 3 610 7 4 987 6 5 1597 5 6 2584 1 7 4181 5 8 6765 6 9 10946 2 10 17711 8 11 28657 1 12 46368 9 -=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=- 1 75025 1 2 121393 1 3 196418 2 4 317811 3 5 514229 5 6 832040 8 7 1346269 4 8 2178309 3 9 3524578 7 10 5702887 1 11 9227465 8 12 14930352 9 1 24157817 8 2 39088169 8 3 63245986 7 4 102334155 6 5 165580141 4 6 267914296 1 7 433494437 5 8 701408733 6 9 1134903170 2 10 1836311903 8 11 2971215073 1 12 4807526976 9  It's hard to display in this forum setting but hopefully you can see what I am doing here. The decimal parity reveals the harmonics and the harmonics repeat every 24 positions. __________________ Squeegee your third-fucking-eye-(Bill Hicks)
|
|
|
|
جواب |
رسائل 23 من 30 في الفقرة |
|
|
|
|
جواب |
رسائل 24 من 30 في الفقرة |
|
|
|
|
جواب |
رسائل 25 من 30 في الفقرة |
|
|
|
|
جواب |
رسائل 26 من 30 في الفقرة |
|
|
|
|
جواب |
رسائل 27 من 30 في الفقرة |
|
|
|
|
جواب |
رسائل 28 من 30 في الفقرة |
|
|
Cerca de 186.000.000 resultados (0,47 segundos)
|
|
|
|
جواب |
رسائل 29 من 30 في الفقرة |
|
|
|
|
جواب |
رسائل 30 من 30 في الفقرة |
|
1/3-24/3 =24 DIAS
25/3-17/4=48 DIAS
18/4-11/5=72 DIAS
12/5-4/6 =96 DIAS
5/6-28/6 =144 DIAS (6.28=2X3.14) NEXO CON EL RADIAN
29/6-22/7=168 DIAS (DIA DE MARIA MAGDALENA 24X6)
23/7-15/8=192 DIAS (ASUNCION DE LA VIRGEN=227 GREGORIANO)
16/8-8/9 =216 DIAS (24X8 FIESTA DE LOS TABERNACULOS)
¿PORQUE LA CONEXION CON CHOLULA?
|
|
|
 أول أول
 سابق
16 a 30 de 30
لاحق سابق
16 a 30 de 30
لاحق
 آخر
آخر

|