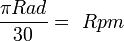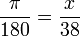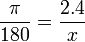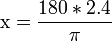|
|
General: RADIANES (FUERTE RELACION ESOTERICA CON EL GRIAL)
Elegir otro panel de mensajes |
|
|
EL EXAGONO Y LA RELACION CON EL PI=22/7-LAS MATEMATICAS CONFIRMAN LA RELACION EXAGONAL CON MARIA LA MAGDALENA EN EL MISMO DIA DE SU DIA EN LA IGLESIA CATOLICA, OSEA EL 22 DE JULIO (22/7)
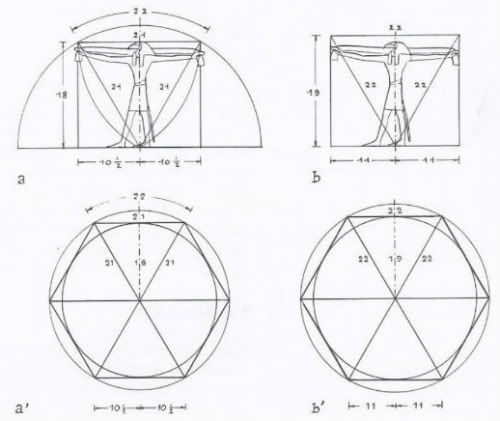 Temple of Man Schwaller de Lubicz page 177 Serpents in the Sky by John Anthony West Temple of Man Schwaller de Lubicz page 177 Serpents in the Sky by John Anthony West
Noten que tenemos el SECTOR CIRCULAR, en un contexto matematico exagonal, la relacion matematica 22/11. Sabemos que la longitud de la circunferencia es igual al numero PI=3.14=22/7 por el DIAMETRO=RADIO*2 del circulo. En un contexto a que tenemos segun la figura superior la LONGITUD DE ARCO (PI/3-RADIANES) que es igual a 22 si hacemos las matematicas:
LONG. CIRC.=3.14*DIAMETRO=3.14*2*RADIO=22/7*2*21=22/7*2*7*3=(22*2*7*3)/7=22*6
LONG. CIRC.=22*6=132=33*4 (IMPRESIONANTE RELACION DEL NUMERO 33)
Noten que estamos haciendo referencia al exagono y es obvia su interrelacion con el planeta Mercurio, que insisto, esta interrelacionada con la ESTRELLA DE DAVID, OSEA EL HIJO DEL MISMO DAVID, QUE FUE EL REY SOL-O-MON. El 33, insisto, es una referencia a los dos triangulos, de la estrella de 6 puntas. Ahora, si la longitud del arco es igual a PI/3 (RADIANES) tenemos la relacion:
22/21=22/(7*3)=(22/7)/3=PI/3
IMPRESIONANTE DE QUE BELLAS SON LAS MATEMATICAS.
LA MISMA PALABRA REVOLU-SION ES UNA REFERENCIA AL NUMERO PI (LONGITUD DE LA CIRCUNFERENCIA ES IGUAL A PI X DIAMETRO.)
|
|
|
|
|
EL EXAGONO, EL NUMERO PI=3:14 Y EL NUMERO DE ORO PHI=1.618
 Temple of Man Schwaller de Lubicz page 177 Serpents in the Sky by John Anthony West Temple of Man Schwaller de Lubicz page 177 Serpents in the Sky by John Anthony West
Sabemos que una ecuacion aproximada de PHI ELEVADO AL CUADRADO (2.618033) ES LA SIGUIENTE:
PHI ELEVADO AL CUADRADO=(6/5)*3.1416..
OSEA QUE PHI=RAIZ CUADRADA DE ((6/5)*3.1416)
SI CONSIDERAMOS EL COCIENTE APROXIMADO DE PI=22/7 NOS QUEDA
=(5/6)*(22/7)=(5*22)/(6*7)=(110/2)/(3*7)=55/21 (NUMEROS SECUENCIALES DE LA SERIE DE FIBONACCI)
2.61904761905
VEMOS QUE ES UNA BUENA APROXIMACION DE PHI AL CUADRADO=2.618
FI=PHI=NUMERO DE ORO=1.618033
171. Salmos 45:9: Hijas de reyes están entre tus ilustres; Está la REINA a tu diestra con oro de Ofir.
SO-FI-A/SABIDURIA/S-OFI-A/FI-L-OFI-A
REINA VESTIDA CON ORO DE O-FI-R
201. Romanos 11:33: ¡Oh profundidad de las riquezas de la sabiduría y de la ciencia de Dios! ¡Cuán insondables son sus juicios, e inescrutables sus caminos!
| Rom 11:33 O the depth of the riches both of the wisdom and knowledge of God! how unsearchable are his judgments, and his ways past finding out! |
|
|
|
|
|
σοφια sophia {sof-ee'-ah} from 4680; TDNT - 7:465,1056; n f AV - wisdom 51; 51 1) wisdom, broad and full of intelligence; used of the knowledge of very diverse matters 1a) the wisdom which belongs to men 1a1) spec. the varied knowledge of things human and divine, acquired by acuteness and experience, and summed up in maxims and proverbs 1a2) the science and learning 1a3) the act of interpreting dreams and always giving the sagest advice 1a4) the intelligence evinced in discovering the meaning of some mysterious number or vision 1a5) skill in the management of affairs 1a6) devout and proper prudence in intercourse with men not disciples of Christ, skill and discretion in imparting Christian truth 1a7) the knowledge and practice of the requisites for godly and upright living 1b) supreme intelligence, such as belongs to God 1b1) to Christ 1b2) the wisdom of God as evinced in forming and executing counsels in the formation and government of the world and the scriptures For Synonyms see entry 5826
Gematria: 781
SO-PHI-A
|
|
|
|
|
Radián
De Wikipedia, la enciclopedia libre
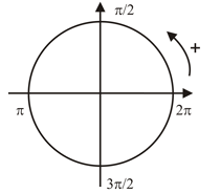
El radián es la unidad de ángulo plano en el Sistema Internacional de Unidades. Representa el ángulo central en una circunferencia y abarca un arco cuya longitud es igual a la del radio. Su símbolo es rad. Hasta 1995 tuvo la categoría de unidad suplementaria en el Sistema Internacional de Unidades, junto con el estereorradián. A partir de ese año, y hasta el momento presente, ambas unidades figuran en la categoría de unidades derivadas.
Esta unidad se utiliza primordialmente en física, cálculo infinitesimal, trigonometría, goniometría, etc.
El ángulo formado por dos radios de una circunferencia, medido en radianes, es igual a la longitud del arco que delimitan los radios; es decir, θ = s/r, donde θ es ángulo, s es la longitud del arco, y r es el radio. Por tanto, el ángulo completo,  , que subtiende una circunferencia de radio r, medido en radianes, es: , que subtiende una circunferencia de radio r, medido en radianes, es:

El radián es una unidad sumamente útil para medir ángulos, puesto que simplifica los cálculos, ya que los más comunes se expresan mediante sencillos múltiplos o divisores de π.
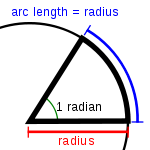
El radián es la unidad natural en la medida de los ángulos. Por ejemplo, la función seno de un ángulo "x" expresado en radianes cumple:
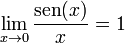
Análogamente los desarrollos Taylor de las funciones seno y coseno son:
donde x se expresa en radianes.
- La equivalencia entre grados sexagesimales y radianes es: π rad = 180°
- La equivalencia entre grados centesimales y radianes es: π rad = 200g
La tabla muestra la conversión de los ángulos más comunes.
| Grados |
0° |
30° |
45° |
60° |
90° |
120° |
135° |
150° |
180° |
210° |
225° |
240° |
270° |
300° |
315° |
330° |
360° |
| Radianes |
0 |
π/6 |
π/4 |
π/3 |
π/2 |
2π/3 |
3π/4 |
5π/6 |
π |
7π/6 |
5π/4 |
4π/3 |
3π/2 |
5π/3 |
7π/4 |
11π/6 |
2π |
Otras unidades de medida de ángulos convencionales son el grado sexagesimal, el grado centesimal y, en astronomía, la hora.
- El Radián tiene una unidad derivada llamada π Radian por segundo (πRad/s). Esta tiene una equivalencia con las Rpm. Las equivalencias se pueden calcular fácilmente con la ecuación que sigue:
- De Rpm a πRad
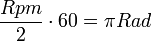 que con la ecuación simplificada: que con la ecuación simplificada:
- De πRad a Rpm
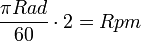 que con la ecuación simplificada: que con la ecuación simplificada: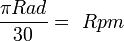
Conversiones entre grados y radianes[editar · editar código]
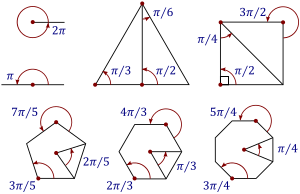
Ángulos de los polígonos más comunes medidos en radianes, expresados como fracciones de π.

Tabla de conversión entre grados sexagesimales y radianes.
Los grados y los radianes son dos diferentes sistemas para medir ángulos. Un ángulo de 360° equivale a 2π radianes; un ángulo de 180° equivale a π radianes (recordemos que el número π ≈ 3,14159265359…).
Las equivalencias de los principales ángulos se muestran en las siguientes figuras:
Para convertir grados en radianes o viceversa, partimos de que 180° equivalen a π radianes; luego planteamos una regla de tres y resolvemos.
Convertir 38° a radianes. radian × 38º 38º radian /180º = 0.21 radianes.
Primero planteamos la regla de tres. Nótese que la x va arriba, en la posición de los radianes.
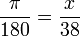
Despejamos x, también simplificamos.

Por último obtenemos el equivalente decimal:
x = 0,6632 radianes.
Convertir 2,4 radianes a grados.
Primero planteamos la regla de tres. Nótese que la x va abajo, en la posición de los grados.
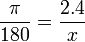
Despejamos x.
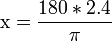
Por último obtenemos el equivalente decimal:
x = 137.5099°"
|
|
|
|
|

Temple of Man Schwaller de Lubicz page 177 Serpents in the Sky by John Anthony WestEn realidad el SECRETO ESTA EN LA RELACION 22/7=PI. Sabemos que en un circulo hay 2*PI RADIANES.
22/21=PI/3
PI=3*22/21=22/7
DEL MONSTRUOSO NUMERO 22/7 SACAMOS MATEMATICAMENTE EL DISEÑO DEL RADIAN. BIBLIA ES SINONIMO DE MATEMATICAS PARA MALDICION DE LOS EGOLATRAS.
|
|
|
|
|
|
La Gran Pirámide y el espacio
You are here: Home / La Gran Pirámide y el espacio
El codo real y el metro
La relación entre el codo real y el metro ha sido establecida por los estudios egiptológicos realizados hasta ahora, que se han basado en la medida de varas de madera con marcas en codos reales. El resultado obtenido es 1 codo real = 0,5236 m.
Al respecto, se produce un hecho desconcertante: 0,5236 equivale, a la vez, a Π/6 y a Φ2/5, ya que 3,1416 / 6 = 0,5236 y también 2,6180 / 5 = 0,5236.
Es decir, si dividimos el Número Π entre 6, nos da el mismo resultado que si dividimos el cuadrado del Número de Oro entre 5. Y en ambos casos obtenemos lo que mide un codo real ¡en metros!
Es más, si dibujamos una circunferencia de 1 metro de diámetro y inscribimos un hexágono en la misma, el arco de circunferencia que corresponde a un lado de ese hexágono es igual a 1 codo real (fig. 16).

Figura 16. La relación geométrica entre el codo real y el metro.
El resultado es muy desconcertante porque nos obliga a preguntarnos: ¿el codo real podía obtenerse geométricamente a partir del metro?
¿El metro en la Gran Pirámide?
Una vez reconstruido el modelo de la Gran Pirámide, lo analizamos minuciosamente. Y uno de los resultados más excepcionales obtenidos fue la longitud de la arista. Esta longitud que era especialmente significativa porque elevaba el monumento hacia el cielo, medía exactamente ¡218,00 metros!
Es decir, parecía como si la Gran Pirámide hubiera sido diseñada, a la vez, en codos reales y en metros, ya que las dos principales longitudes que definían su forma se expresaban en números enteros: el lado de la base medía 440 codos reales y la arista, 218 metros.
¿Se podía tratar de una casualidad?
El análisis de las medidas de la Cámara del Rey, que se mantiene intacta en el interior del monumento, insistía triplemente en la presencia de medidas exactas en metros: La altura sobre el zócalo [1] es 43,00 m. La diagonal del muro mayor de la Cámara del Rey mide 12,00 m. Y el volumen de la Cámara es de 321,00 m3.
Por si no fuese suficiente, la suma de la base (440 cr) y la altura (280 cr) de la Gran Pirámide es igual a 720 cr, una medida que coincide exactamente con 377,00 m. Y además da la casualidad que el 377 es el número 14º de la Serie de Fibonacci.

Figura 17. La Cámara del Rey de la Gran Pirámide.
Ante la insistencia de tantas medidas en metros, es obligado que nos preguntemos: ¿los sacerdotes-arquitectos de la Gran Pirámide conocían el metro y lo usaron como segunda unidad de medida al proyectar el monumento?
Para intentar responder a esta pregunta, veamos si las medidas en metros nos proponen juegos numéricos.
Sumemos las 9 longitudes obtenidas: las 4 aristas (4 x 218 = 872 m), más las 4 diagonales de los muros mayores de la Cámara del Rey (4 x 12 = 48 m), más su altura sobre el zócalo (43 m). Resultará 963 m. Y, curiosamente, esta cifra es el triple de 321, el número que expresa el volumen de la Cámara del Rey en m3.
¿Se trata de otra casualidad?
Al llegar a este punto, como había números que establecían juegos entre ellos o se repetían insistentemente en la Gran Pirámide, recordé que Pitágoras [2] estudió en Egipto, donde vivió entre 10 y 20 años, y donde fue ungido sacerdote, por lo que tuvo acceso a sus conocimientos. Por eso no es extraño que el llamado Teorema de Pitágoras se halle en la Gran Pirámide.
Pitágoras y los pitagóricos afirmaban que “todo es número“, por lo que consideraban a los números como divinidades o como entidades abstractas preexistentes e independientes de su unidad de medida.
Este hecho viene confirmado por nuestra cotidiana práctica mental. Si yo levanto la mano y te muestro fijamente la palma abierta con los 5 dedos extendidos, no te preguntaras si es que te estoy saludando, sino que inconscientemente pensarás en el número 5, con independencia de que te esté mostrando 5 dedos.
Lo importante, pues, es el número, no la unidad que expresa. Tanto da que te muestre 5 dedos o 5 lápices, tú pensarás en el número 5.
Basándonos en este concepto, encontraremos otro importante juego numérico, asociado a las medidas enteras que definen el monumento: el lado de la base de 440 cr y la arista de 218 m. La pirámide tiene 4 lados y 4 aristas. El número que se obtiene de la suma de los 4 lados es 4 x 440 = 1.760; y el que resulta de la suma de las 4 aristas es 4 x 218 = 872. Su diferencia es igual a 888.
Y el 888 es el número que contiene la clave de la Gran Pirámide de Keops.
La ley matemática del número 888
Una vez reconstruido el modelo original de la Gran Pirámide y a la vista de los resultados que se iban obteniendo, resultaba imprescindible estudiarlo con detalle. En un primer análisis era necesario obtener y estudiar sus magnitudes: el perímetro, la superficie y el volumen.
A partir de la concepción abstracta del número que nos llega desde los pitagóricos, me decidí a tomar las magnitudes de la Gran Pirámide simplemente como números, con independencia de la unidad de medida que designaban. Y ello dio como resultado una extraña ley asociada a un número singular: el 888.
En la adjunta Tabla de la Gran Pirámide (fig. 18) las magnitudes se hallan en codos reales y en metros. La investigación desarrollada me permitió concluir lo ya intuido: la relación entre el codo real y el metro que los sacerdotes-arquitectos de la Gran Pirámide usaron en el monumento fue 1 codo real = Φ2/5 metros, o lo que es lo mismo, 1 codo real = 2,61803399/5 metros = 0,52360680 metros.
Esta relación es, pues, la que se aplica entre ambas unidades de medida, tanto en el perímetro de la Gran Pirámide, como en su superficie o en su volumen. Por tanto y como es lógico, para transformar codos reales en metros se ha multiplicado la medida en codos reales por 0,52360680; para hacerlo de cr2 a m2, se ha multiplicado los cr2 dos veces por esa cifra, es decir, por su cuadrado; y para pasar de cr3 a m3 se ha multiplicado los cr3 tres veces por la cifra antedicha, es decir, por su cubo.

Figura 18. La Tabla de la Gran Pirámide, con sus magnitudes que cumplen la Ley del 888.
En la tabla adjunta (fig. 18) también se puede aplicar la teoría de conjuntos. Si pongo sobre la mesa una cesta con 3 plátanos, 5 naranjas y 8 manzanas, puedo decir que en la cesta tengo 16 frutas, porque estoy sumando elementos distintos de similar naturaleza.
Es por ello, que tanto si entendemos que las magnitudes son sólo números, como si aplicamos la teoría de conjuntos, podemos sumar codos reales o metros con independencia de que sean lineales, cuadrados o cúbicos. Y es por ello que también podemos sumar los números de las magnitudes obtenidas tal como se hallan en la última columna de la Tabla, donde se suman codos reales y metros.
Observemos las sumas resultantes de cada una de las tres columnas: 18.301.722, 2.671.509 y 20.973.231. Separemos las cifras de 4 en 4, es decir, tomémoslas en unidades de 10.000. En la primera columna resultarán 1.830 y 1.722; en la segunda, 267 y 1.509; y en la tercera, 2.097 y 3.231. Sumemos los números 2 a 2 y obtendremos, en todas ellas, múltiplos de 888, ya que se cumple 1.830 + 1.722 = 3.552 = 888 x 4, y también, 267 + 1.509 = 1.776 = 888 x 2, y finalmente, 2.097 + 3.231 = 5.328 = 888 x 6.
A pesar de haber consultado a cualificados matemáticos, aún ninguno de ellos se ha podido explicar esta ley tan sorprendente. No sabemos cómo los sacerdotes-arquitectos egipcios pudieron establecerla. Y tampoco cómo pudieron llegar a construir la Gran Pirámide a partir de ella.
En el supuesto de que hoy conociéramos la Ley del 888 y, a partir de ella, intentásemos construir una pirámide que tuviera un perímetro, una superficie y un volumen prefijados, sólo podríamos hacerlo mediante sucesivas aproximaciones a través del ordenador. Y quién sabe cuánto tiempo necesitaríamos para conseguirlo y si finalmente lo conseguiríamos.
Por tanto, la Ley del 888 presenta un doble enigma:
¿De dónde procedían los conocimientos matemáticos hallados en la Gran Pirámide?
Los sacerdotes-arquitectos de la Gran Pirámide… ¿Cómo consiguieron diseñar el monumento a partir de tener prefijados su perímetro, su superficie y su volumen por la Ley del 888?
Sin embargo, más allá de los enigmas que abre, la Tabla de la Gran Pirámide nos aporta una importante certeza.
La Ley del número 888 ofrece la prueba irrefutable de que la reconstrucción del modelo original de la Gran Pirámide es totalmente exacta.
Y esta afirmación se basa en que dicha Ley no se cumpliría si hubiera una desviación en el perímetro de la Gran Pirámide de un solo codo real sobre 8.388 cr, o de un solo codo real cuadrado en su superficie sobre 314.159 cr2, o de un solo codo real cúbico en su volumen sobre 17.979.175 cr3, lo que en este último caso representaría que si la exactitud de la reconstrucción fuera de un 99,999994% no sería suficiente para que la Ley del 888 se cumpliese.
Por tanto… ¡La Ley del 888 certifica la reconstrucción exacta del modelo de la Gran Pirámide en sus medidas originales!
Y la Ley del 888 también confirma que en la Gran Pirámide se usó una unidad de medida prácticamente igual a nuestro metro, que establecía la igualdad ya comentada entre 1 codo real y 0,523606797 metros.
|
|
|
|
|
Tao of the Tau
Tau is the Greek letter T or τ in lower case.

The symbol τ was used in mathematics to represent the golden ratio until the Greek letter Phi (Φ) gained prominance (after the first letter of Phidias, acclaimed sculptor of the Parthenon).
Tau is also known as the symbol representing the ratio of any circle’s circumference to its radius (equal to 2π).
Advocates for τ argue that radius is more fundamental to circles than diameter, and therefore, that τ (circumference divided by radius) is more fundamental than π (circumference divided by diameter). They think this makes formulas written in terms of τ express the mathematics more clearly than with π. -Source
Using τ instead of 2π makes a lot of sense to me:
- A circle is defined as all points in a plane a certain radius away from a center point.
- The unit circle has a radius of 1, not a diameter of 1.
- Angles measured in radians make more sense using τ rather than 2π because τ radians measures a full circle, so 1/4 circle is τ/4, 1/2 circle is τ/2 and so on.

However using τ is really a moot point because π already won the mindshare. However I find it interesting that Tau has been used to represent both the golden ratio (Φ) and the relationship of a circle to its radius (more commonly known as π).
I can think of one other symbol that encodes in its proportions both mathematical ideas: the Great Pyramid. Note that the proportions 4:π and Φ:1 are not taken at the same time but I’ve shown them together for simplicity, so read the left and right halves of the diagram separately.

“The Tau cross is also a symbol of the male or creative side of the deity, and is really a conventionalized form of the phallus.” -Freemasonry and the Ancient Gods by J.S. Ward
Crowley used an inverted Tau on the cover of his book Magick, which was “regarded in serious occult circles as a book of ultimate authority on sexual magic.” -Source

Seen right-side-up, the T is seen as the shape of the cross on which Jesus was crucified.
The TAU cross is preserved to modern Masonry under the symbol of the T square. This appears to be the oldest form of the cross extant.” -The Secret Teachings of All Ages by Manly Hall
There are several instances in the Bible of the Tau cross anticipating the Latin cross:
- The angel of death passed over the children of Israel who painted the Tau mark in goat’s or sheep’s blood above their doors to slay all Egyptian firstborn. This is better known as Passover. See Exodus 11:1 in the Brick Testament.
- The Tau mark was placed upon the foreheads of particular men to save them from being slain in yet another genocidal bloodbath depicted in Ezekiel 9 (unforunately this isn’t illustrated in Lego).
- The summit of Mt. Nebo in Jordan is the location of the Brazen Serpent Monument, featuring a snake wrapped around a Tau cross.

Image by Jerzy Strzelecki under the Creative Commons Attribution-Share Alike 3.0 Unported license.
Mt. Nebo is where Moses saw the promised land of Israel (but wasn’t allowed to go there himself). You can see Jerusalem on a clear day from this monument.
Pope Benedict XVI visited the site on May 9, 2009, gave a speech, and looked out from the top of the mountain in the direction of Jerusalem. -Source
The fiery serpent comes from the Bible (Numbers 21:5-9):
- “And the people spake against God, and against Moses, Wherefore have ye brought us up out of Egypt to die in the wilderness? for there is no bread, neither is there any water; and our soul loatheth this light bread.
- And the LORD sent fiery serpents among the people, and they bit the people; and much people of Israel died.
- Therefore the people came to Moses, and said, We have sinned, for we have spoken against the LORD, and against thee; pray unto the LORD, that he take away the serpents from us. And Moses prayed for the people.
- And the LORD said unto Moses, Make thee a fiery serpent, and set it upon a pole: and it shall come to pass, that every one that is bitten, when he looketh upon it, shall live.
- And Moses made a serpent of brass, and put it upon a pole, and it came to pass, that if a serpent had bitten any man, when he beheld the serpent of brass, he lived.”
Check out this version illustrated with Lego. I like the Brick Testament because it consistently shows the character of this God. In this case God kills his chosen people with snakes because they complained about being hungry and thirsty. It’s easy to forget that and recall only that he healed those who didn’t complain with the Nehushtan as it is also known.
The 25th degree in Scottish Freemasonry is called is The Knight of the Brazen Serpent.
Here is a old masonic jewel that is probably from this degree.

Thanks to Rick for this image
The above image reminds one of the Rod of Asclepius. Here it is as the Star of Life, logo of the emergency medical services worldwide.

Also the emblem of the World Heath Organization underlines the fact that it is a specialized agency of the United Nations with its 33 sector grid laid over the world.

The symbol of a serpent climbing the pole is also a symbol of Kundalini, or life force rising up the spinal column.

These symbols all came from the Crux Ansata, better known as the Ankh. Think of it as a yoni on top of a lingam, or vesica piscis on top of a tau if you will. What better way to symbolize life then through sexual union? This has been pushed into the shadow in the last two thousand years in the West.

Thanks to reader Rick for pointing out that the Hindu Ardhanari is a composite androgynous form of the Hindu god Shiva and his consort Parvati: half male and half female, split down the middle. Note the Ankh is used here as a depiction of both male and female genitalia.

Image from Tantra: Cult of the Feminine by Andre van Lysebeth page 240
The Hindu androgyne reminds me of Baphomet whom the Templars revealed they worshipped under torture by the French Catholics in 1307.

Often mistaken for Satan, Baphomet represents the duality of male and female, as well as Heaven and Hell or night and day signified by the raising of one arm and the downward gesture of the other. -Source
I can’t help remember sex kitten Lady Gaga striking a similar pose in a Masonic Lodge (see Repeating Ones).

Image source
Look closely: Gaga’s left breast (on our right) is pushed up and her right breast is flattened much like Ardhanari. Gaga as Baphomet.

Image by Redtigerxyz under the Creative Commons Attribution 3.0 Unported license
Andre van Lysebeth shows in Tantra that the Om glyph actually represents the sexual act (female on the left and male on the right in this case) with what looks to me like the sun and moon in the upper right:

Image from Tantra: Cult of the Feminine by Andre van Lysebeth page 170
The Ankh is similar to the concept of the Tao in Chinese philosophy and religion. Opposites coming together form a dynamic balance.
Thank you Ian le Cheminant for emailing me this vitally important concept:
I had always associated synchronicity with Carl Jung but recently rereading Lama Anagarika Govinda’s The Inner Structure of the I Ching I was reminded that as a mode of thinking it is profoundly Chinese. Govinda writes: “All our reasoning is based on the law of cause and effect operating as a sequence. The Chinese do not reason so much along this horizontal line from past, through present to future; they reason perpendicularly, from what is in one place now to what is in another place now. In other words, they do not ask why, or from what past causes, a certain set of things is happening now; they ask, ‘What is the meaning of these things happening at this moment?’ The word Tao is the answer to this question. The present situation within and around oneself is Tao, for the present moment is life. Our memory of the past is contained in it as well as the potentiality for the future.”

Squaring the circle also comes to mind as a larger resolution of opposites, in the case of heaven and earth.

Earth Sun Moon by Scott Onstott
Pi brings together the linear and the curved, the limited and the unlimited, the human and the divine.

The Sword and the Ring by Scott Onstott
Slight dyslexia is all you need to get from Angels to Angles. In many areas of mathematics angles are measured in radians rather than degrees. One radian is equal to about 57 degrees (57.2957795…).
360 degrees = 2π or 6.283185… radians. An angle of 1 radian results in an arc with a length equal to the radius of the circle.
Tau is the 19th letter of the Greek alphabet. Three Taus therefore have a value of 3 x 19 = 57.

Triple Tau is an important Masonic symbol.
“This emblem, placed in the center of a Triangle and Circle – both emblems of Deity – constitutes the jewel of the Royal Arch as practiced in England, where it is so highly esteemed as to be called the “emblem of all emblems,” and “the grand emblem of Royal Arch Masonry.” -Source

Image by PeRshGo under the Creative Commons Attribution-Share Alike 3.0 Unported license.
The Royal Arch Degree Jew-el has a Star of David composed of two interlocking triangles (male and female) and a triple Tau at the bottom. This reminds me of the phrase triple bottom line or Hermes Trismegistus.

This ancient Alchemical emblem found in the ruins of Pompei suggests that the Star of David is a metaphor for the sexual act, a fact covered up by the SATOR magic square (see Paternoster Squares).
Robert Fowler discovered a cipher in Shakespeare’s sonnets dedication poem that requires one understand the Royal Arch Degree jewel in order to decode it. It’s a fascinating intellectual journey that I won’t belabour in this post.

However I will mention the decoded message refers to eternal life and a diagram that appears to depict Orion, an obelisk, a pyramid, the Star of David, and rays of the Sun. It is becoming harder not to see that Francis Bacon was involved in writing the works of “William Shakespeare.”
Listen to Robert Newman on The Shakespeare Project.
The 33rd degree jewel depicts four Taus forming a Greek cross.

“The quadruple tau, moreover, being composed entirely of ‘right angles, horizontals, and perpendiculars,’ contains within itself all the secret signs of Freemasonry, a fact which I am not permitted to further explain. It will, however, be apparent to every ‘bright mason,’ who can soon study them all out for himself.” -Stellar Theology and Masonic Astronomy by Robert Hewitt Brown
I’m not a mason but am bright enough to see at least on one level that the Quadruple Tau cross represents the great cross in the heavens as discussed in my Esoteric Astronomy video. The four beasts corresponding to the fixed signs in the aforementioned alchemical seal and Royal Arch degree jewel support this notion.

Here’s the Hindu version of the 33rd degree jewel: the Sri Yantra aka Sri Chakra. In addition to four taus, it features nine interlocking triangles, just as the 33rd degree jewel shows a nine pointed star and the brazen serpent jewel depicts a nine-pointed star.

Image by N.Manytchkine under the Creative Commons Attribution-Share Alike 3.0 Unported license
That brings me to a couple of very interesting buildings I’ve become aware of that I think encode the Quadruple Tau symbol. First up is Terrace on the Park at 52-11 111th Street in Flushing Meadows Park, Queens, NY. Do you see the solar 52 weeks in a year encoded with all the ones? The building was contructed as a helipad for the 1964 World’s Fair, which I plan to post about another time. One can say it has a special connection with the sky.

Thanks to John Handrinos who lives nearby the park for pointing out many of its secrets in plain sight.
Here is the official video about what goes on inside Terrace on the Park. Lots of people getting married inside Terrace on the Park seems quite appropriate symbolically.
Finally my thanks to Grant Chamberlin who discovered something very interesting about the CitiGroup Center (aka 601 Lexington Ave) in Manhattan.

The square base reminds me of the Quadruple Tau even though it is not highlighted as such.

Grant noticed that there are 32 full panels across the top of the T plus 2 half panels, making a total of 33 panels on each side. Just a coincidence or the Tao of the Tau?
©2012 SIPS Productions Inc. – All Rights Reserved.
|
|
|
|
|
DÍAS DE CELEBRACIÓN DE π

Entre los que se encuentran el mismo 22 de Julio (22/7=3.1428), y curiosamente también el 21 de diciembre…

Pero el día oficial de π es el 3-14…
25/4 es el dia de SAN JUAN MARCOS, DIA NUMERO 227 DEL CALENDARIO COPTO |
|
|
|
|
Día Pi (π)
El día Pi es una fiesta no oficial que celebra la constante matemática pi (π). Se celebra el 14 de marzo en los países que siguen el formato mes / día que corresponden con los dígitos 3/14.
En los países que siguen el formato de fecha día / mes, la fiesta es después, el 22 de julio y se llama El día Pi por aproximación. Esto resulta de que el 22 de julio, o sea, el 22/7 es el valor aproximado de π (22 /7 = 3,14).
El día Pi el 14 de marzo también coincide con el cumpleaños de Albert Einstein. Otras fechas especiales del calendario del día Pi en 2015: Será la única vez del siglo que la celebración del sábado, será un Pi muy especial: Sólo se da una vez cada 100 años. Este año, no sólo el mes y el día de la fecha (3/14) corresponden a los dígitos de la constante matemática, los dígitos del año también lo hacen. Si se escribe la fecha en el formato mes / día / año, entonces los dígitos de la fecha 3/14/15 se corresponden con los 5 primeros dígitos de pi: 3.1415.

Pero eso no es todo. El día Pi de este año va un paso más allá. A las 9:26:53 am y las 09:26:53 pm, la fecha y la hora se corresponden exactamente a los 10 primeros dígitos de pi: 3,141592653. Muchas personas están llamando a este el segundo Pi. Aunque hay un cierto desacuerdo sobre si habrá dos o un segundo Pi. Los más "puristas" creen que sólo puede haber un segundo Pi el de las 9:26:53 am, considerando que a las 09:26:53 pm en el reloj de 24 horas son las 21:26:53.
A este respecto Jeffrey S. Rosenthal, profesor de Estadística de la Universidad de Toronto ha propuesto la designación del instante Pi: El instante exacto en el que la fecha y hora incluyen todos los dígitos de pi.
Cuenta atrás para el Segundo Pi
Una constante antigua y universal Pi (π), es una letra ampliamente conocida y una de las constantes matemáticas más reconocida, el diámetro en el espacio euclidiano o la relación del área de un círculo con su radio al cuadrado. El valor de PI es aproximadamente igual a 3.14159265, pero es un número irracional y su representación decimal nunca termina.
Día paléndromo
El día Pi fue fundado por Larry Shaw y se celebró por primera vez en 1988 en el Exploratorium de San Francisco.
El público y el personal del museo marcharon alrededor de un espacio circular y comiern pasteles de frutas.
Los estudiantes, los matemáticos y los entusiastas de las matemáticas de todo el mundo celebran el Día Pi participando en actividades y concursos alrededor de pi que incluye hacer y comer empanadas, convertir números tales como el tiempo o la edad de cada uno usando pi, y recitar los dígitos de pi o ver la famosa película en blanco y negro Pi (1988) de Darren Aronofsk
Días alternativos Pi y aproximación Pi se pueden celebrar en otras fechas del calendario como:
- 22 de julio: Cuando 22 se divide por 7, resulta igual a 3.14.
- 5 de Abril: Cuando han transcurrido 3,14 meses del año.
- 26 de Abril: La Tierra ha viajado dos radianes de su órbita en el día de hoy (25 de abril en los años bisiestos). Esta se celebra exactamente en el segundo 41 del minuto 23 de la cuarta hora, el 26 de abril o el día 116. (En los años bisiestos, se celebra exactamente en el tercer segundo del segundo minuto de la hora 12 el 25 de abril o el día 116 del año.)
- 10 de november: El día 314 del año (9 de noviembre en años bisiestos).
- 21 de Diciembre, a las 1:13 p.m.: El 355 día del año (20 de diciembre en los años bisiestos), que se celebra a las 1:13 de la aproximación china 355/113.
- http://elsoberadotecnologia.blogspot.com.ar/2015/03/dia-pi.html
22 DE JULIO=DIA DE MARIA MAGDALENA
25 DE ABRIL=DIA DE SAN MARCOS
|
|
|
|
|

squarerootofawesome.bl...
y medida en radianes 2π,
400 × 211 - 104 k - png |

squarerootofawesome.bl...
y medida en radianes 2π,
588 × 604 - 531 k - png |
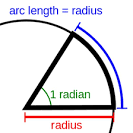
culturacientifica.com
grados equivale un radián?
560 × 560 - 26 k - jpg |

aula.tareasplus.com
Regístrate para ver este video
480 × 360 - 13 k - jpg |
gabitos.com
Arco1.png
220 × 194 - 12 k - png |

fisica3m.blogspot.com
en radianes (medida para
236 × 237 - 9 k - jpg |
angulosimbolosentorno....
grado medido a radianes,
2000 × 1969 - 1951 k - jpeg |
vega00.com
El área del triángulo sera 1/2
449 × 329 - 12 k - jpg |

es.slideshare.net
)1 0 /2 radianes = 90°,
638 × 1181 - 178 k - jpg |

es.slideshare.net
Exprese en radianes los
638 × 903 - 80 k - jpg |
matematicas10-2013.blo...
El ángulo formado por dos
300 × 300 - 31 k - bmp |

es.slideshare.net
π/2 radianes C) π/6,
638 × 479 - 35 k - jpg |

covacha-matematica.blo...
ángulo o radián es la raíz
1525 × 631 - 43 k - jpg |

squarerootofawesome.bl...
Un ángulo de medida 1 se forma
320 × 176 - 6 k - png |

es.slideshare.net
(RAD) 360º=2·pi radianes.
638 × 903 - 85 k - jpg |

fotomat.es
radianes, donde π/2 = 90º.
583 × 530 - 119 k - jpg |

angulosimbolosentorno....
pi radianes
1366 × 768 - 58 k - jpg |

diccio-mates.blogspot.com
Tabla de Conversiones
398 × 359 - 67 k - jpg |

covarida.blogspot.com
Circunferencia en radianes Vs.
1246 × 1600 - 397 k - jpg |
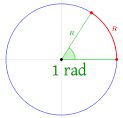
mategmonzonvenet.blogs...
qué es un radián vamos a
387 × 370 - 22 k - png |
|
|
|
|
|
In a 5 by 12 rectangle, one of the diagonals is drawn and circles are inscribed in both right triangles thus formed. Find the distance between the centers of the two circles.
UPDATE!
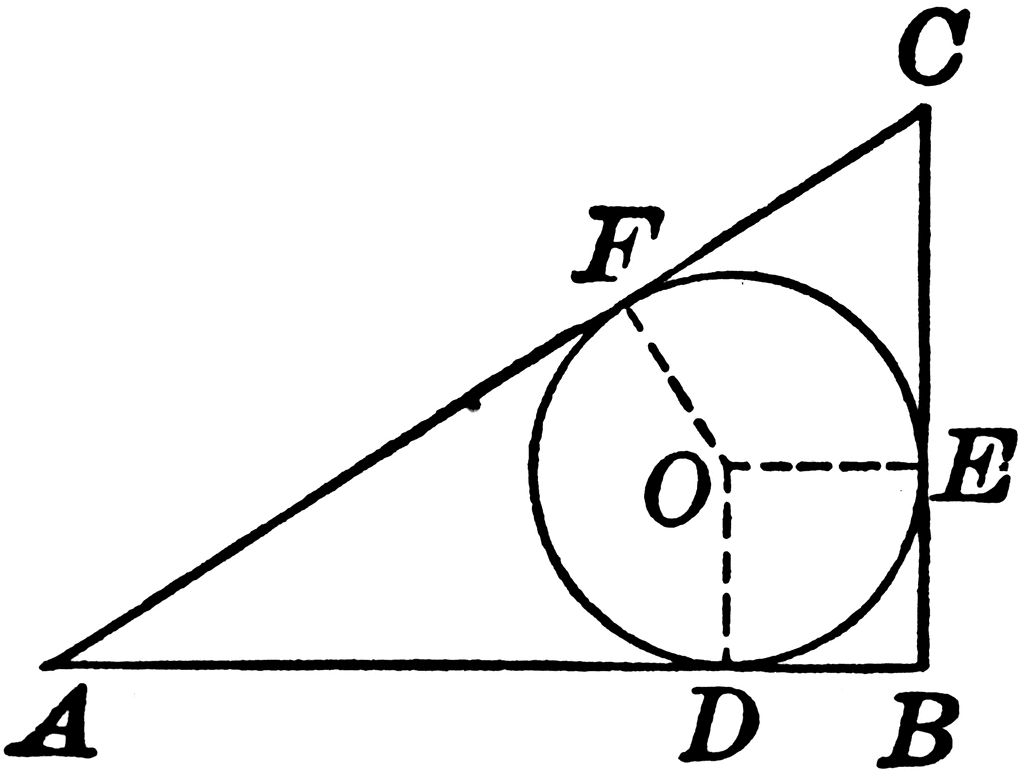 Triangle Formulas : Right Triangle Triangle Formulas : Right TriangleC = A + B = Pi/2 radians = 90 degrees c^2 = a^2 + b^2 P = a + b + c s = (a+b+c)/2 K = ab/2
Particular case: Circle Inscribed in Triangle 3, 4, 5
Circle Inscribed in a Right Triangle
General case: Circle Inscribed in Triangle a, b, cWe can write, r = ab/(a + b + c) with c = sqrt(a^2 + b^2)
d = sqrt((a - 2r)^2+(b - 2r)^2)OR r = (a + b - c)/2 where c = Sqrt(a^2 + b^2)
Then (a - 2r)^2 + (b - 2r)^2 = (c - a)^2 + (c - b)^2 etc |
|
|
|
|
Sinusoidal Waveforms
Generation of Sinusoidal Waveforms
In our tutorials about Electromagnetism, we saw how an electric current flowing through a conductor can be used to generate a magnetic field around itself, and also if a single wire conductor is moved or rotated within a stationary magnetic field, an “EMF”, (Electro-Motive Force) will be induced within the conductor due to this movement.
From this tutorial we learnt that a relationship exists between Electricity and Magnetism giving us, as Michael Faraday discovered the effect of “Electromagnetic Induction” and it is this basic principal that electrical machines and generators use to generate a Sinusoidal Waveform for our mains supply.
In the Electromagnetic Induction, tutorial we said that when a single wire conductor moves through a permanent magnetic field thereby cutting its lines of flux, an EMF is induced in it.
However, if the conductor moves in parallel with the magnetic field in the case of points A and B, no lines of flux are cut and no EMF is induced into the conductor, but if the conductor moves at right angles to the magnetic field as in the case of points C and D, the maximum amount of magnetic flux is cut producing the maximum amount of induced EMF.
Also, as the conductor cuts the magnetic field at different angles between points A and C, 0 and 90o the amount of induced EMF will lie somewhere between this zero and maximum value. Then the amount of emf induced within a conductor depends on the angle between the conductor and the magnetic flux as well as the strength of the magnetic field.
An AC generator uses the principal of Faraday’s electromagnetic induction to convert a mechanical energy such as rotation, into electrical energy, a Sinusoidal Waveform. A simple generator consists of a pair of permanent magnets producing a fixed magnetic field between a north and a south pole. Inside this magnetic field is a single rectangular loop of wire that can be rotated around a fixed axis allowing it to cut the magnetic flux at various angles as shown below.
Basic Single Coil AC Generator

As the coil rotates anticlockwise around the central axis which is perpendicular to the magnetic field, the wire loop cuts the lines of magnetic force set up between the north and south poles at different angles as the loop rotates. The amount of induced EMF in the loop at any instant of time is proportional to the angle of rotation of the wire loop.
As this wire loop rotates, electrons in the wire flow in one direction around the loop. Now when the wire loop has rotated past the 180o point and moves across the magnetic lines of force in the opposite direction, the electrons in the wire loop change and flow in the opposite direction. Then the direction of the electron movement determines the polarity of the induced voltage.
So we can see that when the loop or coil physically rotates one complete revolution, or 360o, one full sinusoidal waveform is produced with one cycle of the waveform being produced for each revolution of the coil. As the coil rotates within the magnetic field, the electrical connections are made to the coil by means of carbon brushes and slip-rings which are used to transfer the electrical current induced in the coil.
The amount of EMF induced into a coil cutting the magnetic lines of force is determined by the following three factors.
- • Speed – the speed at which the coil rotates inside the magnetic field.
- • Strength – the strength of the magnetic field.
- • Length – the length of the coil or conductor passing through the magnetic field.
We know that the frequency of a supply is the number of times a cycle appears in one second and that frequency is measured in Hertz. As one cycle of induced emf is produced each full revolution of the coil through a magnetic field comprising of a north and south pole as shown above, if the coil rotates at a constant speed a constant number of cycles will be produced per second giving a constant frequency. So by increasing the speed of rotation of the coil the frequency will also be increased. Therefore, frequency is proportional to the speed of rotation, ( ƒ ∝ Ν ) where Ν = r.p.m.
Also, our simple single coil generator above only has two poles, one north and one south pole, giving just one pair of poles. If we add more magnetic poles to the generator above so that it now has four poles in total, two north and two south, then for each revolution of the coil two cycles will be produced for the same rotational speed. Therefore, frequency is proportional to the number of pairs of magnetic poles, ( ƒ ∝ P ) of the generator where P = is the number of “pairs of poles”.
Then from these two facts we can say that the frequency output from an AC generator is:

Where: Ν is the speed of rotation in r.p.m. P is the number of “pairs of poles” and 60 converts it into seconds.
Instantaneous Voltage
The EMF induced in the coil at any instant of time depends upon the rate or speed at which the coil cuts the lines of magnetic flux between the poles and this is dependant upon the angle of rotation, Theta ( θ ) of the generating device. Because an AC waveform is constantly changing its value or amplitude, the waveform at any instant in time will have a different value from its next instant in time.
For example, the value at 1ms will be different to the value at 1.2ms and so on. These values are known generally as the Instantaneous Values, or Vi Then the instantaneous value of the waveform and also its direction will vary according to the position of the coil within the magnetic field as shown below.
Displacement of a Coil within a Magnetic Field

The instantaneous values of a sinusoidal waveform is given as the “Instantaneous value = Maximum value x sin θ ” and this is generalized by the formula.
Where, Vmax is the maximum voltage induced in the coil and θ = ωt, is the angle of coil rotation.
If we know the maximum or peak value of the waveform, by using the formula above the instantaneous values at various points along the waveform can be calculated. By plotting these values out onto graph paper, a sinusoidal waveform shape can be constructed.
In order to keep things simple we will plot the instantaneous values for the sinusoidal waveform at every 45o of rotation giving us 8 points to plot. Again, to keep it simple we will assume a maximum voltage, VMAX value of 100V. Plotting the instantaneous values at shorter intervals, for example at every 30o (12 points) or 10o (36 points) for example would result in a more accurate sinusoidal waveform construction.
Sinusoidal Waveform Construction
| Coil Angle ( θ ) |
0 |
45 |
90 |
135 |
180 |
225 |
270 |
315 |
360 |
| e = Vmax.sinθ |
0 |
70.71 |
100 |
70.71 |
0 |
-70.71 |
-100 |
-70.71 |
-0 |

The points on the sinusoidal waveform are obtained by projecting across from the various positions of rotation between 0o and 360o to the ordinate of the waveform that corresponds to the angle, θ and when the wire loop or coil rotates one complete revolution, or 360o, one full waveform is produced.
From the plot of the sinusoidal waveform we can see that when θ is equal to 0o, 180o or 360o, the generated EMF is zero as the coil cuts the minimum amount of lines of flux. But when θ is equal to 90o and 270o the generated EMF is at its maximum value as the maximum amount of flux is cut.
Therefore a sinusoidal waveform has a positive peak at 90o and a negative peak at 270o. Positions B, D, F and H generate a value of EMF corresponding to the formula e = Vmax.sinθ.
Then the waveform shape produced by our simple single loop generator is commonly referred to as a Sine Wave as it is said to be sinusoidal in its shape. This type of waveform is called a sine wave because it is based on the trigonometric sine function used in mathematics, ( x(t) = Amax.sinθ ).
When dealing with sine waves in the time domain and especially current related sine waves the unit of measurement used along the horizontal axis of the waveform can be either time, degrees or radians. In electrical engineering it is more common to use the Radian as the angular measurement of the angle along the horizontal axis rather than degrees. For example, ω = 100 rad/s, or 500 rad/s.
Radians
The Radian, (rad) is defined mathematically as a quadrant of a circle where the distance subtended on the circumference equals the radius (r) of the circle. Since the circumference of a circle is equal to 2π x radius, there must be 2π radians around a 360o circle, so 1 radian = 360o/2π = 57.3o. In electrical engineering the use of radians is very common so it is important to remember the following formula.
Definition of a Radian

Using radians as the unit of measurement for a sinusoidal waveform would give 2π radians for one full cycle of 360o. Then half a sinusoidal waveform must be equal to 1π radians or just π (pi). Then knowing that pi, π is equal to 3.142 or 22÷7, the relationship between degrees and radians for a sinusoidal waveform is given as.
Relationship between Degrees and Radians
Applying these two equations to various points along the waveform gives us.

The conversion between degrees and radians for the more common equivalents used in sinusoidal analysis are given in the following table.
Relationship between Degrees and Radians
| Degrees |
Radians |
Degrees |
Radians |
Degrees |
Radians |
| 0o |
0 |
135o |
3π
4
|
270o |
3π
2
|
| 30o |
π
6
|
150o |
5π
6
|
300o |
5π
3
|
| 45o |
π
4
|
180o |
π |
315o |
7π
4
|
| 60o |
π
3
|
210o |
7π
6
|
330o |
11π
6
|
| 90o |
π
2
|
225o |
5π
4
|
360o |
2π |
| 120o |
2π
3
|
240o |
4π
3
|
|
|
The velocity at which the generator rotates around its central axis determines the frequency of the sinusoidal waveform. As the frequency of the waveform is given as ƒ Hz or cycles per second, the waveform has angular frequency, ω, (Greek letter omega), in radians per second. Then the angular velocity of a sinusoidal waveform is given as.
Angular Velocity of a Sinusoidal Waveform
and in the United Kingdom, the angular velocity or frequency of the mains supply is given as:

in the USA as their mains supply frequency is 60Hz it is therefore: 377 rad/s
So we now know that the velocity at which the generator rotates around its central axis determines the frequency of the sinusoidal waveform and which can also be called its angular velocity, ω. But we should by now also know that the time required to complete one revolution is equal to the periodic time, (T) of the sinusoidal waveform.
As frequency is inversely proportional to its time period, ƒ = 1/T we can therefore substitute the frequency quantity in the above equation for the equivalent periodic time quantity and substituting gives us.

The above equation states that for a smaller periodic time of the sinusoidal waveform, the greater must be the angular velocity of the waveform. Likewise in the equation above for the frequency quantity, the higher the frequency the higher the angular velocity.
Sinusoidal Waveform Example No1
A sinusoidal waveform is defined as: Vm = 169.8 sin(377t) volts. Calculate the RMS voltage of the waveform, its frequency and the instantaneous value of the voltage after a time of 6ms.
We know from above that the general expression given for a sinusoidal waveform is:

Then comparing this to our given expression for a sinusoidal waveform above of Vm = 169.8 sin(377t) will give us the peak voltage value of 169.8 volts for the waveform.
The waveforms RMS voltage is calculated as:

The angular velocity (ω) is given as 377 rad/s. Then 2πƒ = 377. So the frequency of the waveform is calculated as:

The instantaneous voltage Vi value after a time of 6mS is given as:

Note that the phase angle at time t = 6mS is given in radians. We could quite easily convert this to degrees if we wanted to and use this value instead to calculate the instantaneous voltage value. The angle in degrees will therefore be given as:

Sinusoidal Waveform
Then the generalised format used for analysing and calculating the various values of a Sinusoidal Waveform is as follows:
A Sinusoidal Waveform

In the next tutorial about Phase Difference we will look at the relationship between two sinusoidal waveforms that are of the same frequency but pass through the horizontal zero axis at different time intervals. |
|
|
|
|
Tao of the Tau
Tau is the Greek letter T or τ in lower case.

The symbol τ was used in mathematics to represent the golden ratio until the Greek letter Phi (Φ) gained prominance (after the first letter of Phidias, acclaimed sculptor of the Parthenon).
Tau is also known as the symbol representing the ratio of any circle’s circumference to its radius (equal to 2π).
Advocates for τ argue that radius is more fundamental to circles than diameter, and therefore, that τ (circumference divided by radius) is more fundamental than π (circumference divided by diameter). They think this makes formulas written in terms of τ express the mathematics more clearly than with π. –Source
Using τ instead of 2π makes a lot of sense to me:
- A circle is defined as all points in a plane a certain radius away from a center point.
- The unit circle has a radius of 1, not a diameter of 1.
- Angles measured in radians make more sense using τ rather than 2π because τ radians measures a full circle, so 1/4 circle is τ/4, 1/2 circle is τ/2 and so on.

However using τ is really a moot point because π already won the mindshare. However I find it interesting that Tau has been used to represent both the golden ratio (Φ) and the relationship of a circle to its radius (more commonly known as π).
I can think of one other symbol that encodes in its proportions both mathematical ideas: the Great Pyramid. Note that the proportions 4:π and Φ:1 are not taken at the same time but I’ve shown them together for simplicity, so read the left and right halves of the diagram separately.

“The Tau cross is also a symbol of the male or creative side of the deity, and is really a conventionalized form of the phallus.” –Freemasonry and the Ancient Gods by J.S. Ward
Crowley used an inverted Tau on the cover of his book Magick, which was “regarded in serious occult circles as a book of ultimate authority on sexual magic.” –Source

Seen right-side-up, the T is seen as the shape of the cross on which Jesus was crucified.
The TAU cross is preserved to modern Masonry under the symbol of the T square. This appears to be the oldest form of the cross extant.” –The Secret Teachings of All Ages by Manly Hall
There are several instances in the Bible of the Tau cross anticipating the Latin cross:
- The angel of death passed over the children of Israel who painted the Tau mark in goat’s or sheep’s blood above their doors to slay all Egyptian firstborn. This is better known as Passover. See Exodus 11:1 in the Brick Testament.
- The Tau mark was placed upon the foreheads of particular men to save them from being slain in yet another genocidal bloodbath depicted in Ezekiel 9 (unforunately this isn’t illustrated in Lego).
- The summit of Mt. Nebo in Jordan is the location of the Brazen Serpent Monument, featuring a snake wrapped around a Tau cross.

Image by Jerzy Strzelecki under the Creative Commons Attribution-Share Alike 3.0 Unported license.
Mt. Nebo is where Moses saw the promised land of Israel (but wasn’t allowed to go there himself). You can see Jerusalem on a clear day from this monument.
Pope Benedict XVI visited the site on May 9, 2009, gave a speech, and looked out from the top of the mountain in the direction of Jerusalem. –Source
The fiery serpent comes from the Bible (Numbers 21:5-9):
- “And the people spake against God, and against Moses, Wherefore have ye brought us up out of Egypt to die in the wilderness? for there is no bread, neither is there any water; and our soul loatheth this light bread.
- And the LORD sent fiery serpents among the people, and they bit the people; and much people of Israel died.
- Therefore the people came to Moses, and said, We have sinned, for we have spoken against the LORD, and against thee; pray unto the LORD, that he take away the serpents from us. And Moses prayed for the people.
- And the LORD said unto Moses, Make thee a fiery serpent, and set it upon a pole: and it shall come to pass, that every one that is bitten, when he looketh upon it, shall live.
- And Moses made a serpent of brass, and put it upon a pole, and it came to pass, that if a serpent had bitten any man, when he beheld the serpent of brass, he lived.”
Check out this version illustrated with Lego. I like the Brick Testament because it consistently shows the character of this God. In this case God kills his chosen people with snakes because they complained about being hungry and thirsty. It’s easy to forget that and recall only that he healed those who didn’t complain with the Nehushtan as it is also known.
The 25th degree in Scottish Freemasonry is called is The Knight of the Brazen Serpent.
Here is a old masonic jewel that is probably from this degree.

Thanks to Rick for this image
The above image reminds one of the Rod of Asclepius. Here it is as the Star of Life, logo of the emergency medical services worldwide.

Also the emblem of the World Heath Organization underlines the fact that it is a specialized agency of the United Nations with its 33 sector grid laid over the world.

The symbol of a serpent climbing the pole is also a symbol of Kundalini, or life force rising up the spinal column.

These symbols all came from the Crux Ansata, better known as the Ankh. Think of it as a yoni on top of a lingam, or vesica piscis on top of a tau if you will. What better way to symbolize life then through sexual union? This has been pushed into the shadow in the last two thousand years in the West.

Thanks to reader Rick for pointing out that the Hindu Ardhanari is a composite androgynous form of the Hindu god Shiva and his consort Parvati: half male and half female, split down the middle. Note the Ankh is used here as a depiction of both male and female genitalia.

Image from Tantra: Cult of the Feminine by Andre van Lysebeth page 240
The Hindu androgyne reminds me of Baphomet whom the Templars revealed they worshipped under torture by the French Catholics in 1307.

Often mistaken for Satan, Baphomet represents the duality of male and female, as well as Heaven and Hell or night and day signified by the raising of one arm and the downward gesture of the other. –Source
I can’t help remember sex kitten Lady Gaga striking a similar pose in a Masonic Lodge (see Repeating Ones).

Image source
Look closely: Gaga’s left breast (on our right) is pushed up and her right breast is flattened much like Ardhanari. Gaga as Baphomet.

Image by Redtigerxyz under the Creative Commons Attribution 3.0 Unported license
Andre van Lysebeth shows in Tantra that the Om glyph actually represents the sexual act (female on the left and male on the right in this case) with what looks to me like the sun and moon in the upper right:

Image from Tantra: Cult of the Feminine by Andre van Lysebeth page 170
The Ankh is similar to the concept of the Tao in Chinese philosophy and religion. Opposites coming together form a dynamic balance.
Thank you Ian le Cheminant for emailing me this vitally important concept:
I had always associated synchronicity with Carl Jung but recently rereading Lama Anagarika Govinda’s The Inner Structure of the I Ching I was reminded that as a mode of thinking it is profoundly Chinese. Govinda writes: “All our reasoning is based on the law of cause and effect operating as a sequence. The Chinese do not reason so much along this horizontal line from past, through present to future; they reason perpendicularly, from what is in one place now to what is in another place now. In other words, they do not ask why, or from what past causes, a certain set of things is happening now; they ask, ‘What is the meaning of these things happening at this moment?’ The word Tao is the answer to this question. The present situation within and around oneself is Tao, for the present moment is life. Our memory of the past is contained in it as well as the potentiality for the future.”

Squaring the circle also comes to mind as a larger resolution of opposites, in the case of heaven and earth.

Earth Sun Moon by Scott Onstott
Pi brings together the linear and the curved, the limited and the unlimited, the human and the divine.

The Sword and the Ring by Scott Onstott
Slight dyslexia is all you need to get from Angels to Angles. In many areas of mathematics angles are measured in radians rather than degrees. One radian is equal to about 57 degrees (57.2957795…).
360 degrees = 2π or 6.283185… radians. An angle of 1 radian results in an arc with a length equal to the radius of the circle.
Tau is the 19th letter of the Greek alphabet. Three Taus therefore have a value of 3 x 19 = 57.

Triple Tau is an important Masonic symbol.
“This emblem, placed in the center of a Triangle and Circle – both emblems of Deity – constitutes the jewel of the Royal Arch as practiced in England, where it is so highly esteemed as to be called the “emblem of all emblems,” and “the grand emblem of Royal Arch Masonry.” –Source

Image by PeRshGo under the Creative Commons Attribution-Share Alike 3.0 Unported license.
The Royal Arch Degree Jew-el has a Star of David composed of two interlocking triangles (male and female) and a triple Tau at the bottom. This reminds me of the phrase triple bottom line or Hermes Trismegistus.

This ancient Alchemical emblem found in the ruins of Pompei suggests that the Star of David is a metaphor for the sexual act, a fact covered up by the SATOR magic square (see Paternoster Squares).
Robert Fowler discovered a cipher in Shakespeare’s sonnets dedication poem that requires one understand the Royal Arch Degree jewel in order to decode it. It’s a fascinating intellectual journey that I won’t belabour in this post.

However I will mention the decoded message refers to eternal life and a diagram that appears to depict Orion, an obelisk, a pyramid, the Star of David, and rays of the Sun. It is becoming harder not to see that Francis Bacon was involved in writing the works of “William Shakespeare.”
Listen to Robert Newman on The Shakespeare Project.
The 33rd degree jewel depicts four Taus forming a Greek cross.

“The quadruple tau, moreover, being composed entirely of ‘right angles, horizontals, and perpendiculars,’ contains within itself all the secret signs of Freemasonry, a fact which I am not permitted to further explain. It will, however, be apparent to every ‘bright mason,’ who can soon study them all out for himself.” –Stellar Theology and Masonic Astronomy by Robert Hewitt Brown
I’m not a mason but am bright enough to see at least on one level that the Quadruple Tau cross represents the great cross in the heavens as discussed in my Esoteric Astronomy video. The four beasts corresponding to the fixed signs in the aforementioned alchemical seal and Royal Arch degree jewel support this notion.

Here’s the Hindu version of the 33rd degree jewel: the Sri Yantra aka Sri Chakra. In addition to four taus, it features nine interlocking triangles, just as the 33rd degree jewel shows a nine pointed star and the brazen serpent jewel depicts a nine-pointed star.

Image by N.Manytchkine under the Creative Commons Attribution-Share Alike 3.0 Unported license
That brings me to a couple of very interesting buildings I’ve become aware of that I think encode the Quadruple Tau symbol. First up is Terrace on the Park at 52-11 111th Street in Flushing Meadows Park, Queens, NY. Do you see the solar 52 weeks in a year encoded with all the ones? The building was contructed as a helipad for the 1964 World’s Fair, which I plan to post about another time. One can say it has a special connection with the sky.

Thanks to John Handrinos who lives nearby the park for pointing out many of its secrets in plain sight.
Here is the official video about what goes on inside Terrace on the Park. Lots of people getting married inside Terrace on the Park seems quite appropriate symbolically.
http://www.secretsinplainsight.com/2012/01/16/tao-of-the-tau/ |
|
|
|
|
|
The definition of 1 radian. The red line (radius) and blue line (arc length) are the same length. By Stannered, CC-SA-BY-3.0 |
|
|
|
|
Radians are another way to measure angles.
There are 2*pi radians in a full turn so 360 degrees = 2*pi radians
180 degress = pi radians
90 degrees = pi/2 radians etc
Quite often we talk about measures of radians in terms of multiples (or fractions) of pi.
To convert from degrees to radians you divide by 180 and multiply by pi.
To convert from radians to degrees you do the reverse and divide by pi and multiply by 360.
The term "two radians" therefore is the size of an angle. We can think of it in degrees if that makes more sense by converting it as described above.
2/pi*180 = about 114.6 degrees.
If you are doing any calculus you should always make sure you use radians for your angles.
|
|
|
 Primer Primer
 Anterior
3 a 17 de 122
Siguiente Anterior
3 a 17 de 122
Siguiente Último
Último
|
|
| |
|
|
©2024 - Gabitos - Todos los derechos reservados | |
|
|





















 Image from The Contiunuum Encyclopedia of Symbols by Udo Becker
Image from The Contiunuum Encyclopedia of Symbols by Udo Becker








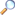
 , que subtiende una
, que subtiende una 
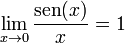


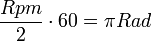 que con la ecuación simplificada:
que con la ecuación simplificada:
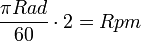 que con la ecuación simplificada:
que con la ecuación simplificada: