|
|
Cerca de 480.000 resultados

es.dreamstime.com
Código digital binario
1300 × 1390 - 786k - jpg |

cmapspublic2.ihmc.us
-de-tecnologia-digital-gl.
1200 × 927 - 246k - jpg |

canstockphoto.es
verde, digital, binario
450 × 320 - 43k - jpg |

es.dreamstime.com
Ciudad digital binaria, fondo
1300 × 960 - 200k - jpg |

es.dreamstime.com
Extracto del indicador digital
1300 × 957 - 313k - jpg |

es.dreamstime.com
Tecnología digital originada
1300 × 1009 - 404k - jpg |

canstockphoto.es
3D, mundo, mapa, binario,
450 × 351 - 53k - jpg |

blog.fundacionmontemad...
Código binario
281 × 400 - 216k - png |

portafolio-09.blogspot...
ocho digitos binarios se
303 × 227 - 24k - jpeg |

ciberescuela103vargasd...
en tecnología digital y
1200 × 900 - 292k - jpg |

curiosidades.batanga.com
Electronica-sistema-binario-y-
657 × 768 - 83k - jpg |

canstockphoto.es
digital, binario, código,
450 × 470 - 67k - jpg |

tecnologiaeinformatica...
sistema binario
199 × 197 - 12k - jpg |

es.123rf.com
binario tecnología digital
1350 × 954 - 170k - jpg |

es.dreamstime.com
Ciudad abstracta binaria
1300 × 1065 - 140k - jpg |

curiosidades.batanga.com
Electronica-sistema-binario-y-
630 × 473 - 50k - jpg |

ensvrinconlealnuevedos...
Cronómetro: El sistema binario
1024 × 1024 - 419k - png |

tecnologia-crito-rey.w...
El sistema binario, en
640 × 480 - 518k - jpg |

es.clipart.me
de la tecnología digital
379 × 269 - 19k - jpg |

es.vectorhq.com
de la tecnología digital
450 × 318 - 45k - jpg |
|
|
|
|
|
 Si cortamos la trompeta obtenemos la forma de la campana
 |
Click para ampliar |
/slides/7th_seal_angels_given_trumpets_cloisters_apocalypse.jpg) 7 - trompetas del apocalipsis, 7 sellos  Funcion discreta de Gauss - trompeta La discreta kernel gaussiano (rojo), en comparación con la muestra del núcleo de Gauss (negro) para las escalas  Trompeta de trompa - Elefante - Aleph-ante   Seno - Teta - Theta valor Griego 9 sentido horario boton - mujer Seno (trigonometría) - Wikipedia, la enciclopedia libre
 |
Click para ampliar |
 Simbolo del dia de la tierra letra Theta - Teta -fertilidad - instaurado en 19-69 Earth Day - Wikipedia, the free encyclopedia  33 =1111 33 =1111 Componente angulo acuario centro de la galaxia  Diosa de la fertilidad - espiral - arco  Cybeles diosa de la fertilidad, muerte y regeneracion, entre los pilares con espirales y rombos -vesica pisicis. 16 Tetas - numero del hipercubo Rodeada por Cerberus el guardian del inframundo 3 cabezas de perro. Debajo Satan
Última edición por IndigoMerovingio; 20-abr-2012 a las 16:11
|
|
|
|
|
 Ondas electromagnéticas Ondas electromagnéticas
En 1886, el físico alemán Heinrich Hertz puso a prueba la teoría creada por un físico teórico escocés llamado James Clerk Maxwell en 1865. Maxwel se dio cuenta que todos los fenómenos eléctricos (rayos en una tormenta eléctrica, la corriente en un cable o las pequeñas descargas que se general al quitarse un sweater) podrían relacionarse con los fenómenos magnéticos conocidos (imanes, movimiento de brújulas). Maxwell unificó la electricidad y el magnetismo en su teoría electromagnética, lo que permite entender fenómenos eléctricos y magnéticos como dos manifestaciones de un mismo fenómeno. Posteriormente esta teoría fue escrita en lenguaje moderno como una teoría cuántica que hoy llamamos electrodinámica cuántica (pero esa es otra historia). La teoría de Maxwell consiste en un set de cuatro ecuaciones que permiten describir cualquier fenómeno eléctrico y magnético (además de usarse para un clásico chiste, adornar autos eléctricos y hacer sufrir a todo estudiante de física por varios años!) Una de las predicciones de las ecuaciones de Maxwell es que el movimiento de partículas cargadas eléctricamente debería generar ondas, de la misma manera que la caída de una hoja en una posa de agua generará ondas en la superficie que se propagan en todas direcciones. La historia se parece a la de Peter Higgs (también escocés) postulando una idea para resolver un problema haciendo una predicción que permitiría testear la validez de la nueva idea en experimentos (en el caso de Higgs es el famoso bosón que parece haber sido descubierto en el CERN). Al contrario de Higgs, Maxwell no alcanzó a ver la confirmación de su predicción (murió en 1879), lograda por Hertz siete años más tarde. Hertz demostró que Maxwell tenía razón al proponer que campos eléctricos y magnéticos se propagan como ondas que se mueven a la velocidad de la luz. Hertz también nos enseñó que sólo basta tomar una partícula cargada (como un electrón) y agitarla para generar estas ondas electromagnéticas (tal como señalan las ecuaciones de Maxwel). Gracias a la teoría de Maxwell y los experimentos de Hertz ahora entendemos que la luz es un tipo particular de onda electromagnética, de la misma forma ondas de radio, microondas, rayos X, infrarojos y ultravioleta también son ondas electromagnéticas. La única diferencia entre estos tipos de ondas es el número de vibraciones por segundo, lo que en física se llama frecuencia (número de oscilaciones por segundo) y la unidad de frecuencia es el hertz (Hz) en honor a Heinrich. Es por eso que cada estación de radio se identifica con una determinada frecuencia en el dial, típicamente varios millones de hertz o megahertz denotado MHz (mega significa 1 millón). Ondas de mayor frecuencias son también ondas con más energía y los físicos han clasificado las ondas de acuerdo a su frecuencia ya que eso permite estimar su energía. Las ondas de radio son las menos energéticas y al otro lado del llamado espectro electromagnético se ubican los peligrosos rayos gamma (producidos por ejemplo en explosiones nucleares).
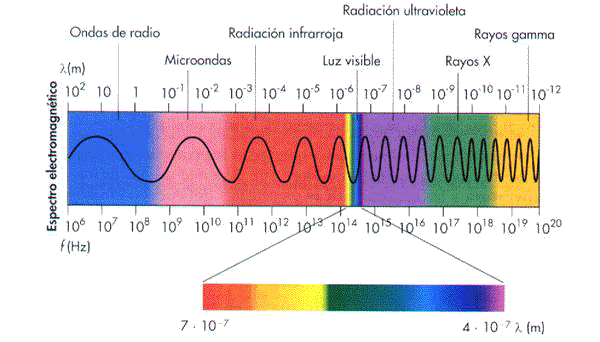
Se llama espectro electromagnético a los diferentes tipos de ondas clasificadas de acuerdo a su frecuencia (o energía).
La figura del espectro electromagnético muestra los nombres de los diferentes tipos de radiación y es posible notar una pequeña banda cerca del centro que corresponde a la luz visible. Esta es la única región que los humanos podemos ver con nuestros ojos! También puede verse en el zoom de esta pequeña banda que los extremos del rango visual son el rojo (baja energía) y el violeta (alta energía), y los colores corresponden al patrón que vemos en un arcoiris. La radiación justo antes de la visible algo menos energética es la radiación infrarroja (es la que usa el control remoto de la TV, los lentes de visión nocturna y que algunas serpientes, entre otros animales, pueden percibir haciéndolos excelentes cazadores), y la que sigue a la radiación visible es la que viene después del violeta, por lo tanto es más energética, es lo que llamamos rayos ultravioleta (tan dañinos para nuestros ojos). Dado que nuestros ojos son sensibles a una región tan limitada del espectro y muchas cosas ocurren en rangos fuera de la radiación visible los científicos han creado instrumentos para medir los otros tipos de radiación. Comúnmente cuando hablamos de telescopios nos referimos a telescopios ópticos que sólo son útiles para estudiar luz visible, para estudiar radiación de otras frecuencias (o energías) se usan telescopios de rayos X y gamma, telescopios infrarrojos, etc. algunos de los cuales son telescopios espaciales que se encuentran en órbita. En un post anterior hablamos de varios telescopios poco convencionales.
Volviendo a las ondas, hoy en día nuestras comunicaciones dependen del uso de las ondas electromagnéticas incluyendo celulares, wi-fi, radio, y comunicaciones satelitales. Los electrones que generan las ondas que usamos para comunicarnos son agitados por esos dispositivos que llamamos antenas. Vivimos rodeados de antenas en cada esquina además de la antena portátil de nuestros dispositivos electrónicos. Las ondas electromagnéticas nos rodean como un legado del gran Maxwell al que hemos aprendido a controlar y usar en nuestro diario vivir.

Einstein describiendo su teoría general de la relatividad
Ondas gravitacionales
En 1915, Einstein publicó teoría general de la relatividad, en la que nos enseñó que el espaciotiempo es flexible y se deforma ante la presencia de objetos masivos como el Sol (más detalles en este post anterior). Una pregunta inmediata que surge ante esta idea de un espaciotiempo flexible es ¿qué pasaría si un objeto tan masivo como para deformar el espaciotiempo se mueve rápidamente? ¿podría la agitación de objetos muy masivos generar ondas en analogía a las ondas producidas por Hertz? La respuesta a esta última pregunta es afirmativa (en teoría). Un interesante ejercicio académico de todo estudiante de física es tomar las ecuaciones de la relatividad general y mostrar que una perturbación del espacio (equivalente a la hoja cayendo en la posa de agua) se propaga a la velocidad de la luz en todas direcciones y el campo gravitacional obedece la misma ecuación que las ondas de Maxwell. Estas ondas gravitacionales son una predicción de la teoría de Einstein, sin embargo hasta la fecha no han sido confirmadas experimentalmente. Uno de los motivos es que se necesita agitar rápidamente una masa enorme para generar una onda gravitacional, por lo cual es algo imposible de hacer de manera artificial en un laboratorio. El otro motivo es que sus efectos serían muy pequeños.

paso de una onda gravitacional
En concreto una onda gravitacional haría que los objetos se contraigan y estiren a su paso. El efecto sería muy pequeño, pero podría amplificarse con el estudio de objeto de gran extensión por lo que observatorios de ondas gravitacionales como LIGO (Laser Interferometer Gravitational-wave Observatory) en EEUU consisten en dos largos brazos perpendiculares (4 km cada uno) al final de los cuales hay un espejo. Un láser mide la distancia a cada espejo, la que aumentará y disminuirá alternadamente en cada brazo ante el paso de una onda gravitacional. Dado que otros fenómenos podrían producir una señal parecida a una onda gravitacional, se construyeron dos de estos observatorios en EEUU, uno en Hanford (estado de Washington) y otro en Livingston (Louisiana), ya que así una onda gravitacional debe detectarse al mismo tiempo y tener las mismas características en ambos observatorios.

vista aérea de LIGO en Livingston, donde se aprecia la extensión de sus brazos perpendiculares de 4 km. cada uno.
Hasta la fecha no existe confirmación de la existencia de estas ondas gravitacionales, sin embargo los científicos han encontrado muchos fenómenos astrofísicos violentos que podrían generarlas. En 1974, el físico Russell Hulse y el astrofísico Joseph Taylor, Jr. descubrieron un sistema formado por dos estrellas de neutrones que orbitan un centro de masa común. Una estrella de neutrones es un objeto muy masivo pero compacto con un radio de unos 10 km. (es lo que queda al final de la vida de una estrella muy masiva) y que no es visible con telescopios convencionales por lo que usaron radiotelescopios para medir las ondas de radio emitidas por este tipo de estrellas. Sus mediciones permitieron notar que la órbita no se mantenía constante y que al pasar el tiempo la distancia entre las estrellas disminuía, es decir, con cada órbita ambas estrellas perdían un poco de energía por lo cual se acercaban lentamente. Cálculos permitieron verificar que el cambio medido correspondía al esperado si el sistema estuviese perdiendo energía en forma de ondas gravitacionales, es decir, las mediciones se ajustan con gran precisión a los predichos por la relatividad general. Este descubrimiento se considera una verificación indirecta de la existencia de ondas gravitacionales y dió el Premio Nobel a Hulse y Taylor en 1993. Sin embargo los físicos siguen a la espera de poder medir el paso directo de una onda gravitacional en sus observatorios. Es importante mencionar que LIGO no es el único observatorio de ondas gravitacionales, GEO600 en Alemania, TAMA en Japón y VIRGO en Italia están también a la caza de estas vibraciones del espaciotiempo. Dos interesantes videos que describen detalles del funcionamiento de estos observatorios se encuentran aquí y aquí (lamentablemente en inglés), los que en la práctica corresponden a interferómetros gigantes. Existe también un proyecto llamado LISA, que es equivalente a LIGO pero en órbita en torno a la Tierra lo que permitiría brazos mucho más largos entre la fuente de láser y los espejos. Sin embargo el proyecto tiene complicaciones técnicas y económicas por lo que no hay certeza que sea alguna vez lanzado al espacio. Ya he dicho antes que la ciencia hoy de hace con migajas, las que probablemente no alcanzarán para estos proyectos tan ambiciosos.
En abril de 2011, un grupo de astrónomos de EEUU y España descubrió que un par de estrellas llamadas enanas blancas orbitan en torno a un centro común separadas a una distancia menor que la separación Tierra-Luna (las enanas blancas son los restos muy calientes y moribundos de estrellas no muy masivas como nuestro Sol, son como las brasas de un fuego extinguido). Lo notable de este sistema es que los astrónomos determinaron que las estrellas completan cada órbita en menos de 13 minutos! Esta enorme velocidad orbital convierte a este sistema (llamado SDSS J065133.338+284423.37, sí el nombre no es muy atractivo por lo que se le llama J0651) en un excelente laboratorio para testear la predicción de Einstein ya que el par del estrellas del sistema binario J0651 está siendo agitado violentamente (el paper se encuentra en arXiv).

Simulación de un sistema binario emitiendo ondas gravitacionales
NOTEN LA SIMILITUD CON LA LETRA S / SERPIENTE / "AGUJERO DE GUSANO" / VESICA PISCIS=JUAN 21:11
Esta semana las ondas gravitacionales estuvieron en los medios ya que el mismo grupo que descubrió J0651 el año pasado (ahora junto a otros astrónomos) anunciaron que han medido que las estrellas del sistema J0651 se acercan lentamente (paper en arXiv). Este resultado es ya interesante, sin embargo los astrónomos también estimaron la tasa a la que las estrellas se acercan y lo compararon con lo que la relatividad general de Einstein predice: el resultado es que las enanas blancas del sistema J0651 se acercan exactamente como se esperaría de acuerdo a las ecuaciones de Einstein! El paper de este hallazgo está en el proceso de revisión por científicos especializados (el paper fue anunciado a hace menos de una semana), por lo que habrá que esperar para la reacción de la comunidad científica. Sin duda esto es un resultado muy interesante que parece indicar que la teoría de Einstein sigue rigiendo el comportamiento de objetos astrofísicos con gran precisión.
Comentario: muchos medios de noticias científicas han cubierto esta interesante noticia, sin embargo algunos medios hablan de “descubrimiento de ondas gravitacionales”. Aquí hay que tener mucho cuidado ya que este nuevo trabajo, al igual que el de Hulse y Taylor, muestra evidencia sólida de que las ondas gravitacionales son un fenómeno real, sin embargo es evidencia indirecta. Es muy pronto para declarar la observación de ondas gravitacionales, lo que se espera ocurra en alguno de los observatorios en operación o quizás en el futuro en LISA.
Imágenes: NASA, LIGO, ESA.
http://conexioncausal.wordpress.com/2012/09/02/ondas-electromagneticas-y-gravitacionales/
|
|
|
|
|
La luna es codigo del mono o sea la singularidad del centro de la galaxia, mono de moon - Luna, primer dia de la semana moon of Mon-day, Luna de Lun-es. Mon =1 pero tambien 7 los fractales del centro de la galaxia. Las 7 vidas del gato -nebulosa ojo de. Aqui explico de que se trata - mas adelante hay mas informacion. El eje del espiral es el arbolito de navidad que es el arbol de la vida y termina en la estrella pentagonal de Venus. http://www.burbuja.info/inmobiliaria...-post1847.htmlLa Luna esta sin-c-ronizada con el centro de la galaxia, cinc la piedra filosofal Sin era el Dios sumerio de la Luna - C corresponde a 3 por lo tanto Sin-c o Cinc es el nombre de la piedra filosofal, de alli tambien el numero cinc-o, O=15 =1111 Cronizacion de Cronos que es el Dios del tiempo que es, Saturno, Satan el planeta numero 6 de los anillos, el numero del hombre y de la bestia, nuestra rotacion en sentiod antihorario. Satan, Saturno en la mitologia se come a sus hijos, se representa con la guadaña que es la Luna cresciente, la de Lunes. Al aproximarse los espirales en el centro de la galaxia esto se refleja en la Luna creciente len forma de U ya que las dos fuerzas magnetica se unen en el polo haciendo fluctuar el eje de la misma. La estrella de 6 puntas es la de David - el hexagono, la construccion de la abeja, que es el rombo dodecahedro, etc.
Última edición por IndigoMerovingio; 01-abr-2012 a las 19:07
|
|
|
|
|
6+9=15 (BINARIO)=1111=33
11 (BINARIO)=33
15=SATURNO
|
|
|
|
|
|
19/10/2015 15:19
|
NÚMEROS CÚBICOS.
Los números cúbicos son aquellos que obtenemos al elevar al cubo los sucesivos números naturales:
13 = 1; 23 = 8; 33 = 27; .....
Pero también podemos construir estos números geométricamente,
|
|
|

es.walyou.com
2 Alcancia cubo Rubik
521 × 423 - 24k - jpg |

es.wikipedia.org
El interior de un cubo de
232 × 199 - 28k - jpg |

solostocks.com
Cubo Mágico
500 × 500 - 29k - jpg |

pocoseso.com
del Rubik - Cubo Magico -
450 × 338 - 28k - jpg |
Búsquedas relacionadas con cubo magico
EL MISMO "CUBO MAGICO" ES UN HIPERCUBO (HAY UN CUBO MAS CHICO EN EL CENTRO DEL MISMO)
| Reply |
Message 24 of 24 on the subject |
|
El término cuarta dimensión aparece en diversos contextos como la física, las matemáticas y la ciencia ficción. En cada contexto el significado es diferente:
En física, se hace referencia a la cuarta dimensión al hablar del tiempo, principalmente desde el planteamiento de la Teoría de la Relatividad.
En matemática, el concepto aparece asociado o bien a espacios euclídeos de más de tres dimensiones o, más generalmente, a espacios localmente euclídeos o 4-variedades diferenciables.

Hipercubo de 4 dimensiones espaciales girando, tal como se vería proyectado en el espacio tridimensional.
El interés en las dimensiones más altas alcanzó su clímax entre 1870 y 1920.1 En esos años se convirtió en tema frecuente en la literatura fantástica, el arte e incluso algunas teorías científicas. La cuarta dimensión, entendida como dimensión espacial adicional (no como dimensión temporal, como en la teoría de la relatividad) apareció en las obras literarias de Oscar Wilde, Fiódor Dostoyevski, Marcel Proust, H. G. Wells y Joseph Conrad, inspiró algunas obras musicales de Alexander Scriabin, Edgar Varèse y George Antheil y algunas obras plásticas de Pablo Picasso y Marcel Duchamp influyendo en el desarrollo del cubismo. Incluso personajes tan diversos como el psicólogo William James, la escritora Gertrude Stein o el socialista revolucionario Vladimir Lenin se interesaron en el tema.
Igualmente los matemáticos habían estado interesados en el tema al tratar de generalizar los conceptos de la geometría euclídea tridimensional. El matemático Charles L. Dodgson, que enseñó en la Universidad de Oxford, deleitó a generaciones de escolares escribiendo libros, bajo el pseudónimo de Lewis Carroll, que incorporaban algunas ideas sobre la cuarta dimensión. Desde el punto de vista académico, el estudio general de la geometría de la cuarta dimensión en gran parte resultado de los trabajos de Bernhard Riemann. Charles Howard Hinton, matemático y escritor de ciencia ficción británico, acuñó muchos neologismos para describir elementos en la cuarta dimensión. De acuerdo con el Oxford English Dictionary, fue el primero en emplear la palabra tesseract en su libro Una nueva era del pensamiento. También inventó las palabras “kata” (del griego “abajo”) y “ana” (del griego “arriba”) para describir las dos direcciones opuestas en la cuarta dimensión, equivalentes a derecha-izquierda, arriba-abajo, y adelante-atrás.
Los trabajos matemáticos sobre geometrías multidimensionales y geometrías no euclídeas habían sido considerado por los físicos como simples abstracciones matemáticas hasta que Henri Poincaré probó que el grupo de transformaciones de Lorentz que dejaban invariantes las ecuaciones del electromagnetismo podían ser interpretadas como "rotaciones" en un espacio de cuatro dimensiones. Más tarde, los trabajos de Einstein y la interpretación geométrica de estos por parte de Hermann Minkowski llevaron a la aceptación de la cuarta dimensión como una descripción necesaria para explicar los hechos observados relacionados con el electromagnetismo. Sin embargo, aquí la "cuarta dimensión" no era un lugar separado del espacio tridimensional (como en varias de las obras de ficción de la época) ni tampoco una dimensión espacial análoga a las otras tres dimensiones espaciales, sino una dimensión temporal que sólo puede recorrerse hacia el futuro. En la teoría general de la relatividad el campo gravitatorio es explicado como un efecto geométrico de la curvatura de un espacio-tiempo de cuatro dimensiones.
Más tarde, la teoría de Kaluza-Klein propuso que no sólo el campo gravitatorio podía ser interpretado de forma más sencilla como curvatura de un "espacio" de más de tres dimensiones, sino que si se introducía una nueva dimensión espacial enrollada o «compactificada», también el campo electromagnético podía ser interpretado como un efecto geométrico de la curvatura de dimensiones superiores. Así, la Kaluza proponía una teoría de campo unificado del electromagnetismo y la gravedad en un espacio-tiempo de cinco dimensiones, con una dimensión temporal, tres dimensiones espaciales extendidas y una dimensión espacial «compactificada» adicional, que, debido a su condición de compactificada, no era directamente visible pero su efecto era perceptible en forma de campo electromagnético.

Un ángulo recto se describe como un cuarto de una revolución. La Geometría Cartesiana escoge direcciones ortogonales arbitrariamente a través del espacio, lo que significa que cada dirección está en ángulo recto con las demás. Las 3 dimensiones ortogonales del espacio se conocen como altitud, longitud y latitud. La Cuarta Dimensión por lo tanto es la dirección en el espacio con ángulo recto a las 3 direcciones observables.
Un vector espacial es un conjunto de vectores, los cuales podemos imaginarlos como flechas, que proviene de un simple lugar llamado origen (vectores geométricos), que apuntan a otros lugares.
Un punto es un objeto de cero dimensiones. No tiene extensión en el espacio ni propiedades, como una flecha pero sin longitud. Este vector es llamado el vector cero y es el más simple vector espacial.
Una línea es un objeto unidimensional. Si escogemos un cierto vector distinto a cero en una cierta dirección, este vector tiene cierta longitud definida. Ese vector tiene una cabeza en un cierto punto en espacio y una cola en el origen. Si pensamos en estirar que ese vector así sea dos veces su largo, tres veces, etcétera y uniformemente, tomando todas las longitudes posibles (incluso la longitud cero, conseguir el vector cero), conseguiremos una sola línea con una sola dimensión: La de la longitud. Todos los vectores que describen puntos en esta línea serían paralelos. Aunque para visualizar la línea es necesario que ésta tenga un ancho mínimo, sin embargo, una línea de 1D no la tendría.
Un plano es un objeto de dos dimensiones. Tiene longitud y anchura pero no profundidad - algo como una hoja de papel, o más exactamente algo como las imágenes en un televisor común. El pensamiento en un plano en términos de vectores puede ser un poco más desafiante. Si pensamos en tomar un vector y lo movemos de modo que su cola esté tocando la cabeza del primero y esté formando un vector con su cola en el origen y la cabeza en la cabeza del segundo vector colocado de nuevo, tenemos una manera razonable de hablar de vectores de adición. Si tenemos dos vectores que no sean paralelos, podemos hablar de todos los puntos que podemos alcanzar por o solamente el estirar o ningunos de los vectores, y, agregando estos vectores juntos, estos puntos forman un plano.
El espacio, como lo percibimos, es tridimensional. Podemos pensar en poner una línea junto con un plano. Estas líneas son como un emparedado. Para conseguir a un cierto punto en espacio, podemos imaginarnos el viajar encima de la línea y después el movernos a través del plano al punto. Entonces tenemos tres vectores a pensar alrededor, uno a viajar una cierta distancia encima de la línea y dos para conseguir a un cierto punto en espacio.
Para tres rectas ortogonales en el espacio tridimensional (x, y y z) existe una cuarta, normal al espacio, ortogonal a estas tres rectas, que forma un eje p. ej. w.
El producto vectorial es la determinante de una matriz 4×4, donde una de las filas (o columnas) son los vectores unitarios h, i, j y k y las demás (filas o columnas respectivamente) están formadas por las componentes de tres vectores cuadradimensionales cualesquiera, este producto nos dará un cuarto vector perpendicular a estos tres mismos.
La Geometría euclidiana prevé una mayor variedad de formas para existir que en tres dimensiones. Los poliedros tridimensionales son recintos espaciales hechos de caras de dos dimensiones conectadas, los policronos cuadridimensionales son recintos del espacio cuadridimensional hechos de poliedros tridimensionales. Donde en tres dimensiones, hay exactamente cinco poliedros regulares, o los sólidos platónicos, que pueden existir, seis policronos regulares existen en la cuarta dimensión. Cinco de los seis se pueden interpretar como extensiones naturales de los sólidos platónicos, así como el cubo, un sólido platónico, es una extensión del cuadrado de dos dimensiones. El pentachoron está hecho de 5 tetraedros para las caras y 10 caras triangulares, y es el análogo cuadridimensional del tetraedro. El teseracto, o el hipercubo, se compone de 8 caras cúbicas y de 24 cuadrados, y es el politopo cuadridimensional medido. Los teseractos se doblan, la 16-celdas, son el equivalente del octaedro, pues son ambos politopos de cruz. Los politopos de 120 celdas y los de 600 celdas se doblan de igual modo, y son análogos al dodecaedro y al icosaedro, respectivamente. El de 24 celdas es un policrono regular único y que no tiene ningún equivalente tridimensional. Apenas pues la esfera, o 2-esfera, es una superficie de dos dimensiones curvada compuesta de todos los puntos equidistantes de un punto central dado, en un espacio tridimensional, la 3-esfera, una clase de hiperesfera, es el espacio que contiene todos los puntos equidistantes a un punto central dado, en un espacio cuadridimensional. Cada sección transversal tridimensional de un 3-esfera es un 2-esfera.

La analogía dimensional se usa frecuentemente para comprender el salto de una dimensión (en este caso, la tercera dimensión) a una más alta (cuarta dimensión). La analogía dimensional consiste en resolver un problema en n + 1 dimensiones relacionándolo primero con un problema análogo de (n - 1) dimensión, vale decir, "una dimensión menos". E igualmente debe analizarse el caso de cómo se relaciona el problema en n con el de (n + 1) dimensiones, es decir, "una más".
Edwin Abbott Abbott en su libro Planilandia (Flatland) escribe sobre un "ser cuadrado" que vive en un mundo de dos dimensiones, como la superficie de un pedazo de papel. Este "cuadrado" se enfrenta a experimentos de un ser tridimensional. El ser tridimensional es percibido por el "cuadrado" como un ser aparentemente divino, ya que puede poner y quitar objetos de una caja fuerte sin romperla ni abrirla (moviéndolos a través de su tercera dimensión), ver todo desde de la perspectiva de dos dimensiones sea incluido detrás de las paredes (puesto que ve "sobre" Planilandia), y totalmente invisible para los habitantes de Planilandia, puesto que está "arriba" y una dimensión por arriba de las dos dimensiones en las que el cuadrado está atrapado. No obstante, el ser tridimensional podría manifestarse en el mundo de dos dimensiones, pero sólo parcialmente, si fuera una esfera, aparecería como una secuencia de círculos sucesivos "que cambian de tamaño" (intersecciones de la esfera con el plano de dos dimensiones). Aplicando analogía dimensional, uno puede deducir que el ser cuadridimensional sería capaz de hazañas similares de nuestra perspectiva tridimensional.
Rudy Rucker demuestra esto en su novela "Spaceland", en la cual el protagonista encuentra los seres cuadridimensionales que demuestran tales energías. Un uso útil de la analogía dimensional en visualizar la cuarta dimensión está en la proyección. Una proyección es una manera para representar un objeto (n+1)-dimensional en la n-dimensión. Por ejemplo, las pantallas de computadora son de dos dimensiones, y todas las fotografías de objetos tridimensionales son representadas en dos dimensiones puesto que la información de la tercera dimensión (o de la profundidad) no puede ser representada por la pantalla (si el observador se mueve, aleje o acerque, la imagen no cambiará). En este caso, la profundidad se quita y se substituye por la información indirecta. La retina del ojo es un arsenal de dos dimensiones de receptores pero puede permitir que el cerebro perciba la naturaleza de objetos tridimensionales usando la información indirecta (como la perspectiva, el sombreado, visión binocular, etc.).
La perspectiva del uso de los artistas da profundidad tridimensional a los cuadros de dos dimensiones. Asimismo, los objetos en la cuarta dimensión se pueden proyectar matemáticamente a las familiares tres dimensiones, donde pueden entonces ser examinados más convenientemente. En este caso, la "retina de un ojo cuadridimensional" tendría un arsenal de receptores tridimensionales. El ser hipotético con tal ojo percibiría la naturaleza de objetos cuadridimensionales usando la información indirecta contenida en las imágenes que recibe en su retina. La proyección de la perspectiva a partir de cuatro dimensiones produce efectos similares como en el caso tridimensional, tal como la perspectiva.
Esto agrega "profundidad cuadridimensional" a estos cuadros tridimensionales. La analogía dimensional también ayuda a entender tales proyecciones. Por ejemplo, los objetos de dos dimensiones son limitados por límites unidimensionales: un cuadrado es limitado por cuatro bordes o líneas. Los objetos tridimensionales son limitados por superficies de bidimensionales: un cubo es limitado por 6 cuadrados. Aplicando analogía dimensional, uno puede deducir que un cubo cuadridimensional, conocido como teseracto, es limitado por los volúmenes tridimensionales.
Y de hecho, éste es el caso matemáticamente: el teseracto es limitado por 8 cubos. Saber esto es indispensable para entender cómo interpretar una proyección tridimensional del teseracto. Los límites del teseracto proyectan a los volúmenes en la imagen, superficies no simplemente de dos dimensiones. Esto ayuda a entender las características de dichas dimensiones que de otra manera sólo confundirían. De igual manera, el concepto de sombras puede ayudarnos mejor a entender la teoría de cuatro dimensiones. Si usted proyectara una luz sobre objeto tridimensional, éste proyectaría una sombra de dos dimensiones. Por lo tanto la luz en un objeto de dos dimensiones echaría una sombra unidimensional (en un mundo de dos dimensiones), y la luz en un objeto unidimensional en un mundo unidimensional echaría una sombra cero-dimensional, es decir, un punto de la no-luz. Esta idea se puede utilizar en la otra dirección; la luz en un objeto cuadridimensional proyectaría una sombra tridimensional. Como ejemplo, la sombra de un cubo transparente, proyectaría una sombra sobre el papel, de dos cuadrados, unidos por sus vértices con 4 segmentos.
Semejantemente, si era un cubo cuadridimensional iluminado con luz de 4 dimensiones, su sombra sería la de un cubo tridimensional dentro de otro cubo tridimensional. Siendo tridimensionales podemos solamente ver el mundo con nuestros ojos en dos dimensiones; el ser cuadridimensional consideraría el mundo en tres. Así podría, por ejemplo, ver los seis lados de una caja opaca simultáneamente. No solamente eso; también podría ver lo que hay al interior de la caja, como en Planilandia, en donde la esfera ve objetos en el mundo de dos dimensiones y todo dentro de ellos simultáneamente. Análogo, un espectador cuadridimensional vería todos los puntos en nuestro espacio tridimensional simultáneamente, incluyendo la estructura interna de objetos sólidos y de cosas obscurecidos de nuestro punto de vista.
Albert Einstein en su célebre teoría de 1905 de la relatividad especial habló por primera vez del tiempo como una cuarta dimensión y como algo indispensable para ubicar un objeto en el espacio y en un momento determinado. El tiempo en la teoría de la relatividad no es una dimensión espacial más, ya que fijado un punto del espacio-tiempo éste puede ser no alcanzable desde nuestra posición actual, hecho que difiere de la concepción usual de dimensión espacial. Aunque inicialmente se interpretó el tiempo como una "dimensión" matemática necesaria para ubicar un evento u objeto, en la teoría de la relatividad general el tiempo es tratado como una dimensión geométrica más, aunque los objetos materiales no puedan seguir una trayectoria completamente arbitraria a lo largo del tiempo (como por ejemplo "dar la vuelta" y viajar al pasado). La necesidad del tiempo dentro de la teoría de la relatividad es necesaria por dos motivos:
En primer lugar, los objetos no sólo se mueven a través del espacio sino que también lo hacen a través del tiempo, es decir su coordenada temporal aumenta continuamente, por lo que hubo la necesidad de hablar del tiempo ligado al espacio como la cuarta dimensión (en inglés spacetime, en castellano espacio-tiempo). Además el ritmo de avance en la dimensión temporal depende del estado de movimiento del observador, produciéndose una dilatación temporal efectiva para los observadores más rápidos en relación al tiempo medido por un observador estacionario.
En segundo lugar, el carácter intrínseco del espacio-tiempo y su cuatridimensionalidad requiere un modo conceptualmente diferente de tratar la geometría del universo, puesto que una cuarta dimensión implica un espacio plano (bidimensional) que se curva en la teoría de la relatividad general por la acción de la gravedad de la materia originándose la curvatura del espacio-tiempo.
Finalmente cabe añadir que algunas teorías físicas como la teoría de Kaluza-Klein y las teoría de supercuerdas, en sus varias versiones, añaden a las tres dimensiones físicas espaciales entre 1 y 9 dimensiones espaciales adicionales, de tipo compacto; además de la dimensión temporal.
|
|
|
|
|
|
|
6+9=15 (BINARIO)=1111=33
11 (BINARIO)=3
15=SATURNO
|
|
|
|
|
|
|
|
| Reply |
Message 100 of 101 on the subject |
|
|
|
|
| Reply |
Message 101 of 101 on the subject |
|
| Reply |
Message 294 of 296 on the subject |
|
|
|
|
| Reply |
Message 295 of 296 on the subject |
|
|
|
|
| Reply |
Message 296 of 296 on the subject |
|
857. 1 Corintios 11:8 Porque el varón no procede de la MUJER, sino la MUJER del varón, (EL HIJO TIENE ORIGEN EN EL ESPERMATOZOIDE Y NO EN EL OVULO)
858. 1 Corintios 11:9 y tampoco el varón fue creado por causa de la MUJER, sino la MUJER por causa del varón.
859. 1 Corintios 11:10 Por lo cual la MUJER debe tener señal de autoridad sobre su cabeza, por causa de los ángeles.
860. 1 Corintios 11:11 Pero en el Señor, ni el varón es sin la MUJER, ni la MUJER sin el varón;
CORINTIOS / ORION
861. 1 Corintios 11:12 porque así como la MUJER procede del varón, también el varón nace de la MUJER; pero todo procede de Dios.
LA SERPIENTE SE MUERDE LA COLA.
|
|
|
|
|
|
|
|
|
|
|
|
 First First  Previous 2 to 2 of 2 Next Previous 2 to 2 of 2 Next  Last Last  |
|
|
Fermentation - nigredo - bread and wine of Christ    La vesica piscis (vejiga de pez en latín) es un símbolo hecho con dos círculos del mismo radio que se intersecan de manera que el centro de cada círculo está en la circunferencia del otro. Esta forma se denomina también mandorla (que significa "almendra" en italiano).
Se produce el mismo patron. LA SERPIENTE SE MUERDE LA COLA.
EL MISMO CUBO ESTA DISEÑADO EN FUNCION AL NUMERO 12, EN EL CONTEXTO A LAS 12 HORAS DEL RELOJ. EFECTIVAMENTE TENEMOS 4 LINEAS EN LA PARTE SUPERIOR, 4 EN LA PARTE CENTRAL Y 4 LINEAS EN LA INFERIOR (4+4+4=12). EN EL MARCO AL HIPERCUBO, ADONDE TENEMOS 2 CUBOS COMO PODEMOS OBSERVAR EN LA PARTE SUPERIOR, TENEMOS UNA REFERENCIA OBVIA A LAS 24 HORAS DEL DIA, OSEA 12+12=24. ES OBVIO EN ESTE MARCO QUE EL PATRON DEL HIPERCUBO RESPONDE AL DIA DE 24 HORAS. TODO ESTO ES UNA OBVIA REFERENCIA A HECHOS 12:12, OSEA JUAN MARCOS. EL MISMO PATRON EN EL CONTEXTO AL NUMERO 8 DE LA PLAZA DE SAN PEDRO, TAMBIEN RESPONDE AL PATRON DE LAS 24 HORAS= 8*3 HORAS= 1440 MINUTOS= 8*180 MINUTOS= 86400 SEGUNDOS= 8*10800 SEGUNDOS
|
|
| Reply |
Message 280 of 281 on the subject |
|
|
|
| Reply |
Message 281 of 281 on the subject |
|
|
|
|
|
|
|
|

es.walyou.com
2 Alcancia cubo Rubik
521 × 423 - 24k - jpg |

es.wikipedia.org
El interior de un cubo de
232 × 199 - 28k - jpg |

solostocks.com
Cubo Mágico
500 × 500 - 29k - jpg |

pocoseso.com
del Rubik - Cubo Magico -
450 × 338 - 28k - jpg |
Búsquedas relacionadas con cubo magico
EL MISMO "CUBO MAGICO" ES UN HIPERCUBO (HAY UN CUBO MAS CHICO EN EL CENTRO DEL MISMO)
| Reply |
Message 24 of 24 on the subject |
|
El término cuarta dimensión aparece en diversos contextos como la física, las matemáticas y la ciencia ficción. En cada contexto el significado es diferente:
En física, se hace referencia a la cuarta dimensión al hablar del tiempo, principalmente desde el planteamiento de la Teoría de la Relatividad.
En matemática, el concepto aparece asociado o bien a espacios euclídeos de más de tres dimensiones o, más generalmente, a espacios localmente euclídeos o 4-variedades diferenciables.

Hipercubo de 4 dimensiones espaciales girando, tal como se vería proyectado en el espacio tridimensional.
El interés en las dimensiones más altas alcanzó su clímax entre 1870 y 1920.1 En esos años se convirtió en tema frecuente en la literatura fantástica, el arte e incluso algunas teorías científicas. La cuarta dimensión, entendida como dimensión espacial adicional (no como dimensión temporal, como en la teoría de la relatividad) apareció en las obras literarias de Oscar Wilde, Fiódor Dostoyevski, Marcel Proust, H. G. Wells y Joseph Conrad, inspiró algunas obras musicales de Alexander Scriabin, Edgar Varèse y George Antheil y algunas obras plásticas de Pablo Picasso y Marcel Duchamp influyendo en el desarrollo del cubismo. Incluso personajes tan diversos como el psicólogo William James, la escritora Gertrude Stein o el socialista revolucionario Vladimir Lenin se interesaron en el tema.
Igualmente los matemáticos habían estado interesados en el tema al tratar de generalizar los conceptos de la geometría euclídea tridimensional. El matemático Charles L. Dodgson, que enseñó en la Universidad de Oxford, deleitó a generaciones de escolares escribiendo libros, bajo el pseudónimo de Lewis Carroll, que incorporaban algunas ideas sobre la cuarta dimensión. Desde el punto de vista académico, el estudio general de la geometría de la cuarta dimensión en gran parte resultado de los trabajos de Bernhard Riemann. Charles Howard Hinton, matemático y escritor de ciencia ficción británico, acuñó muchos neologismos para describir elementos en la cuarta dimensión. De acuerdo con el Oxford English Dictionary, fue el primero en emplear la palabra tesseract en su libro Una nueva era del pensamiento. También inventó las palabras “kata” (del griego “abajo”) y “ana” (del griego “arriba”) para describir las dos direcciones opuestas en la cuarta dimensión, equivalentes a derecha-izquierda, arriba-abajo, y adelante-atrás.
Los trabajos matemáticos sobre geometrías multidimensionales y geometrías no euclídeas habían sido considerado por los físicos como simples abstracciones matemáticas hasta que Henri Poincaré probó que el grupo de transformaciones de Lorentz que dejaban invariantes las ecuaciones del electromagnetismo podían ser interpretadas como "rotaciones" en un espacio de cuatro dimensiones. Más tarde, los trabajos de Einstein y la interpretación geométrica de estos por parte de Hermann Minkowski llevaron a la aceptación de la cuarta dimensión como una descripción necesaria para explicar los hechos observados relacionados con el electromagnetismo. Sin embargo, aquí la "cuarta dimensión" no era un lugar separado del espacio tridimensional (como en varias de las obras de ficción de la época) ni tampoco una dimensión espacial análoga a las otras tres dimensiones espaciales, sino una dimensión temporal que sólo puede recorrerse hacia el futuro. En la teoría general de la relatividad el campo gravitatorio es explicado como un efecto geométrico de la curvatura de un espacio-tiempo de cuatro dimensiones.
Más tarde, la teoría de Kaluza-Klein propuso que no sólo el campo gravitatorio podía ser interpretado de forma más sencilla como curvatura de un "espacio" de más de tres dimensiones, sino que si se introducía una nueva dimensión espacial enrollada o «compactificada», también el campo electromagnético podía ser interpretado como un efecto geométrico de la curvatura de dimensiones superiores. Así, la Kaluza proponía una teoría de campo unificado del electromagnetismo y la gravedad en un espacio-tiempo de cinco dimensiones, con una dimensión temporal, tres dimensiones espaciales extendidas y una dimensión espacial «compactificada» adicional, que, debido a su condición de compactificada, no era directamente visible pero su efecto era perceptible en forma de campo electromagnético.

Un ángulo recto se describe como un cuarto de una revolución. La Geometría Cartesiana escoge direcciones ortogonales arbitrariamente a través del espacio, lo que significa que cada dirección está en ángulo recto con las demás. Las 3 dimensiones ortogonales del espacio se conocen como altitud, longitud y latitud. La Cuarta Dimensión por lo tanto es la dirección en el espacio con ángulo recto a las 3 direcciones observables.
Un vector espacial es un conjunto de vectores, los cuales podemos imaginarlos como flechas, que proviene de un simple lugar llamado origen (vectores geométricos), que apuntan a otros lugares.
Un punto es un objeto de cero dimensiones. No tiene extensión en el espacio ni propiedades, como una flecha pero sin longitud. Este vector es llamado el vector cero y es el más simple vector espacial.
Una línea es un objeto unidimensional. Si escogemos un cierto vector distinto a cero en una cierta dirección, este vector tiene cierta longitud definida. Ese vector tiene una cabeza en un cierto punto en espacio y una cola en el origen. Si pensamos en estirar que ese vector así sea dos veces su largo, tres veces, etcétera y uniformemente, tomando todas las longitudes posibles (incluso la longitud cero, conseguir el vector cero), conseguiremos una sola línea con una sola dimensión: La de la longitud. Todos los vectores que describen puntos en esta línea serían paralelos. Aunque para visualizar la línea es necesario que ésta tenga un ancho mínimo, sin embargo, una línea de 1D no la tendría.
Un plano es un objeto de dos dimensiones. Tiene longitud y anchura pero no profundidad - algo como una hoja de papel, o más exactamente algo como las imágenes en un televisor común. El pensamiento en un plano en términos de vectores puede ser un poco más desafiante. Si pensamos en tomar un vector y lo movemos de modo que su cola esté tocando la cabeza del primero y esté formando un vector con su cola en el origen y la cabeza en la cabeza del segundo vector colocado de nuevo, tenemos una manera razonable de hablar de vectores de adición. Si tenemos dos vectores que no sean paralelos, podemos hablar de todos los puntos que podemos alcanzar por o solamente el estirar o ningunos de los vectores, y, agregando estos vectores juntos, estos puntos forman un plano.
El espacio, como lo percibimos, es tridimensional. Podemos pensar en poner una línea junto con un plano. Estas líneas son como un emparedado. Para conseguir a un cierto punto en espacio, podemos imaginarnos el viajar encima de la línea y después el movernos a través del plano al punto. Entonces tenemos tres vectores a pensar alrededor, uno a viajar una cierta distancia encima de la línea y dos para conseguir a un cierto punto en espacio.
Para tres rectas ortogonales en el espacio tridimensional (x, y y z) existe una cuarta, normal al espacio, ortogonal a estas tres rectas, que forma un eje p. ej. w.
El producto vectorial es la determinante de una matriz 4×4, donde una de las filas (o columnas) son los vectores unitarios h, i, j y k y las demás (filas o columnas respectivamente) están formadas por las componentes de tres vectores cuadradimensionales cualesquiera, este producto nos dará un cuarto vector perpendicular a estos tres mismos.
La Geometría euclidiana prevé una mayor variedad de formas para existir que en tres dimensiones. Los poliedros tridimensionales son recintos espaciales hechos de caras de dos dimensiones conectadas, los policronos cuadridimensionales son recintos del espacio cuadridimensional hechos de poliedros tridimensionales. Donde en tres dimensiones, hay exactamente cinco poliedros regulares, o los sólidos platónicos, que pueden existir, seis policronos regulares existen en la cuarta dimensión. Cinco de los seis se pueden interpretar como extensiones naturales de los sólidos platónicos, así como el cubo, un sólido platónico, es una extensión del cuadrado de dos dimensiones. El pentachoron está hecho de 5 tetraedros para las caras y 10 caras triangulares, y es el análogo cuadridimensional del tetraedro. El teseracto, o el hipercubo, se compone de 8 caras cúbicas y de 24 cuadrados, y es el politopo cuadridimensional medido. Los teseractos se doblan, la 16-celdas, son el equivalente del octaedro, pues son ambos politopos de cruz. Los politopos de 120 celdas y los de 600 celdas se doblan de igual modo, y son análogos al dodecaedro y al icosaedro, respectivamente. El de 24 celdas es un policrono regular único y que no tiene ningún equivalente tridimensional. Apenas pues la esfera, o 2-esfera, es una superficie de dos dimensiones curvada compuesta de todos los puntos equidistantes de un punto central dado, en un espacio tridimensional, la 3-esfera, una clase de hiperesfera, es el espacio que contiene todos los puntos equidistantes a un punto central dado, en un espacio cuadridimensional. Cada sección transversal tridimensional de un 3-esfera es un 2-esfera.

La analogía dimensional se usa frecuentemente para comprender el salto de una dimensión (en este caso, la tercera dimensión) a una más alta (cuarta dimensión). La analogía dimensional consiste en resolver un problema en n + 1 dimensiones relacionándolo primero con un problema análogo de (n - 1) dimensión, vale decir, "una dimensión menos". E igualmente debe analizarse el caso de cómo se relaciona el problema en n con el de (n + 1) dimensiones, es decir, "una más".
Edwin Abbott Abbott en su libro Planilandia (Flatland) escribe sobre un "ser cuadrado" que vive en un mundo de dos dimensiones, como la superficie de un pedazo de papel. Este "cuadrado" se enfrenta a experimentos de un ser tridimensional. El ser tridimensional es percibido por el "cuadrado" como un ser aparentemente divino, ya que puede poner y quitar objetos de una caja fuerte sin romperla ni abrirla (moviéndolos a través de su tercera dimensión), ver todo desde de la perspectiva de dos dimensiones sea incluido detrás de las paredes (puesto que ve "sobre" Planilandia), y totalmente invisible para los habitantes de Planilandia, puesto que está "arriba" y una dimensión por arriba de las dos dimensiones en las que el cuadrado está atrapado. No obstante, el ser tridimensional podría manifestarse en el mundo de dos dimensiones, pero sólo parcialmente, si fuera una esfera, aparecería como una secuencia de círculos sucesivos "que cambian de tamaño" (intersecciones de la esfera con el plano de dos dimensiones). Aplicando analogía dimensional, uno puede deducir que el ser cuadridimensional sería capaz de hazañas similares de nuestra perspectiva tridimensional.
Rudy Rucker demuestra esto en su novela "Spaceland", en la cual el protagonista encuentra los seres cuadridimensionales que demuestran tales energías. Un uso útil de la analogía dimensional en visualizar la cuarta dimensión está en la proyección. Una proyección es una manera para representar un objeto (n+1)-dimensional en la n-dimensión. Por ejemplo, las pantallas de computadora son de dos dimensiones, y todas las fotografías de objetos tridimensionales son representadas en dos dimensiones puesto que la información de la tercera dimensión (o de la profundidad) no puede ser representada por la pantalla (si el observador se mueve, aleje o acerque, la imagen no cambiará). En este caso, la profundidad se quita y se substituye por la información indirecta. La retina del ojo es un arsenal de dos dimensiones de receptores pero puede permitir que el cerebro perciba la naturaleza de objetos tridimensionales usando la información indirecta (como la perspectiva, el sombreado, visión binocular, etc.).
La perspectiva del uso de los artistas da profundidad tridimensional a los cuadros de dos dimensiones. Asimismo, los objetos en la cuarta dimensión se pueden proyectar matemáticamente a las familiares tres dimensiones, donde pueden entonces ser examinados más convenientemente. En este caso, la "retina de un ojo cuadridimensional" tendría un arsenal de receptores tridimensionales. El ser hipotético con tal ojo percibiría la naturaleza de objetos cuadridimensionales usando la información indirecta contenida en las imágenes que recibe en su retina. La proyección de la perspectiva a partir de cuatro dimensiones produce efectos similares como en el caso tridimensional, tal como la perspectiva.
Esto agrega "profundidad cuadridimensional" a estos cuadros tridimensionales. La analogía dimensional también ayuda a entender tales proyecciones. Por ejemplo, los objetos de dos dimensiones son limitados por límites unidimensionales: un cuadrado es limitado por cuatro bordes o líneas. Los objetos tridimensionales son limitados por superficies de bidimensionales: un cubo es limitado por 6 cuadrados. Aplicando analogía dimensional, uno puede deducir que un cubo cuadridimensional, conocido como teseracto, es limitado por los volúmenes tridimensionales.
Y de hecho, éste es el caso matemáticamente: el teseracto es limitado por 8 cubos. Saber esto es indispensable para entender cómo interpretar una proyección tridimensional del teseracto. Los límites del teseracto proyectan a los volúmenes en la imagen, superficies no simplemente de dos dimensiones. Esto ayuda a entender las características de dichas dimensiones que de otra manera sólo confundirían. De igual manera, el concepto de sombras puede ayudarnos mejor a entender la teoría de cuatro dimensiones. Si usted proyectara una luz sobre objeto tridimensional, éste proyectaría una sombra de dos dimensiones. Por lo tanto la luz en un objeto de dos dimensiones echaría una sombra unidimensional (en un mundo de dos dimensiones), y la luz en un objeto unidimensional en un mundo unidimensional echaría una sombra cero-dimensional, es decir, un punto de la no-luz. Esta idea se puede utilizar en la otra dirección; la luz en un objeto cuadridimensional proyectaría una sombra tridimensional. Como ejemplo, la sombra de un cubo transparente, proyectaría una sombra sobre el papel, de dos cuadrados, unidos por sus vértices con 4 segmentos.
Semejantemente, si era un cubo cuadridimensional iluminado con luz de 4 dimensiones, su sombra sería la de un cubo tridimensional dentro de otro cubo tridimensional. Siendo tridimensionales podemos solamente ver el mundo con nuestros ojos en dos dimensiones; el ser cuadridimensional consideraría el mundo en tres. Así podría, por ejemplo, ver los seis lados de una caja opaca simultáneamente. No solamente eso; también podría ver lo que hay al interior de la caja, como en Planilandia, en donde la esfera ve objetos en el mundo de dos dimensiones y todo dentro de ellos simultáneamente. Análogo, un espectador cuadridimensional vería todos los puntos en nuestro espacio tridimensional simultáneamente, incluyendo la estructura interna de objetos sólidos y de cosas obscurecidos de nuestro punto de vista.
Albert Einstein en su célebre teoría de 1905 de la relatividad especial habló por primera vez del tiempo como una cuarta dimensión y como algo indispensable para ubicar un objeto en el espacio y en un momento determinado. El tiempo en la teoría de la relatividad no es una dimensión espacial más, ya que fijado un punto del espacio-tiempo éste puede ser no alcanzable desde nuestra posición actual, hecho que difiere de la concepción usual de dimensión espacial. Aunque inicialmente se interpretó el tiempo como una "dimensión" matemática necesaria para ubicar un evento u objeto, en la teoría de la relatividad general el tiempo es tratado como una dimensión geométrica más, aunque los objetos materiales no puedan seguir una trayectoria completamente arbitraria a lo largo del tiempo (como por ejemplo "dar la vuelta" y viajar al pasado). La necesidad del tiempo dentro de la teoría de la relatividad es necesaria por dos motivos:
En primer lugar, los objetos no sólo se mueven a través del espacio sino que también lo hacen a través del tiempo, es decir su coordenada temporal aumenta continuamente, por lo que hubo la necesidad de hablar del tiempo ligado al espacio como la cuarta dimensión (en inglés spacetime, en castellano espacio-tiempo). Además el ritmo de avance en la dimensión temporal depende del estado de movimiento del observador, produciéndose una dilatación temporal efectiva para los observadores más rápidos en relación al tiempo medido por un observador estacionario.
En segundo lugar, el carácter intrínseco del espacio-tiempo y su cuatridimensionalidad requiere un modo conceptualmente diferente de tratar la geometría del universo, puesto que una cuarta dimensión implica un espacio plano (bidimensional) que se curva en la teoría de la relatividad general por la acción de la gravedad de la materia originándose la curvatura del espacio-tiempo.
Finalmente cabe añadir que algunas teorías físicas como la teoría de Kaluza-Klein y las teoría de supercuerdas, en sus varias versiones, añaden a las tres dimensiones físicas espaciales entre 1 y 9 dimensiones espaciales adicionales, de tipo compacto; además de la dimensión temporal.
|
|
|
|
2 AL CUBO=8
3 AL CUBO=27
4 AL CUBO=64
5 AL CUBO=125
5 AL CUBO-CUATRO AL CUBO=5*5*5-4*4*4=125-64=61 (EXAGONAL)
4 AL CUBO-TRES AL CUBO= 4*4*4-3*3*3= 37 ("LLAVE DE DAVID")
3 AL CUBO-DOS AL CUBO=3*3*3-2*2*2=19 (EXAGONAL)
2 AL CUBO-UNO AL CUBO=2*2*2-1*1*1=7 (EXAGONAL)
LAS MATEMATICAS SON EXACTAS
APARENTEMENTE, EN ESTE CONTEXTO, LA PUERTA DE LA "CUARTA DIMENCION", EN EL CONTEXTO A LA RELACION DE QUE EL EXAGONO, TAMBIEN ES UN CUBO, EL OCTOGONO, SERIA LA PUERTA DEL HIPERCUBO, OSEA, INSISTO, LA CUARTA DIMENCION.
LAS MATEMATICAS SERIA:
2*2*2*2-1*1*1*1=15
CONSIDERANDO TAMBIEN AL CERO, ES UNA REFERENCIA AL 16, CODIFICADO EN EL MISMO VATICANO, EN EL PLANETA VENUS, EN EL SISTEMA DIGITAL, ETC,ETC.
|
|
|
|
|
|
|
MATRIX="TODOS LOS SISTEMAS DE COMPUTADORAS A NIVEL MUNDIAL ESTAN DISEÑADOS CON EL PATRON 2,8 Y 16 EN UN CONTEXTO A VENUS"
SABEMOS QUE EL CICLO SIDEREO DE VENUS ES IGUAL A 225. TENEMOS QUE 8 POR 225 ES IGUAL A 1800 Y QUE INCLUSO 16*225=3600. OSEA QUE EN ESTE MARCO TENEMOS QUE EL SISTEMA SEXAGECIMAL TIENE ORIGEN EN LOS CICLOS DE VENUS. LO CURIOSO ES QUE TODO EL SISTEMA DIGITAL TIENE RELACION INSISTO, CON DICHOS NUMEROS.
 |
|
8 * 225 = 1800
|
 |
|
16 * 225 = 3600
|
 



EL SISTEMA HEXADECIMAL DE LAS COMPUTADORAS TIENE FUERTE CONNOTACION CON EL "AGUJERO DE GUSANO"
Tabla de conversión entre decimal, binario, hexadecimal y octal[editar]
| Decimal | Binario | Hexadecimal | octal |
| 0 |
00000 |
0 |
0 |
| 1 |
00001 |
1 |
1 |
| 2 |
00010 |
2 |
2 |
| 3 |
00011 |
3 |
3 |
| 4 |
00100 |
4 |
4 |
| 5 |
00101 |
5 |
5 |
| 6 |
00110 |
6 |
6 |
| 7 |
00111 |
7 |
7 |
| 8 |
01000 |
8 |
10 |
| 9 |
01001 |
9 |
11 |
| 10 |
01010 |
A |
12 |
| 11 |
01011 |
B |
13 |
| 12 |
01100 |
C |
14 |
| 13 |
01101 |
D |
15 |
| 14 |
01110 |
E |
16 |
| 15 |
01111 |
F |
17 |
| 16 |
10000 |
10 |
20 |
| 17 |
10001 |
11 |
21 |
| 18 |
10010 |
12 |
22 |
| 19 |
10011 |
13 |
23 |
| 20 |
10100 |
14 |
24 |
| 21 |
10101 |
15 |
25 |
| 22 |
10110 |
16 |
26 |
| 23 |
10111 |
17 |
27 |
| 24 |
11000 |
18 |
30 |
| 25 |
11001 |
19 |
31 |
| 26 |
11010 |
1A |
32 |
| 27 |
11011 |
1B |
33 |
| 28 |
11100 |
1C |
34 |
| 29 |
11101 |
1D |
35 |
| 30 |
11110 |
1E |
36 |
| 31 |
11111 |
1F |
37 |
| 32 |
100000 |
20 |
40 |
| 33 |
100001 |
21 |
41 |
Sistema hexadecimal
De Wikipedia, la enciclopedia libre
El sistema hexadecimal (a veces abreviado como Hex, no confundir con sistema sexagesimal) es el sistema de numeración posicional que tiene como base el 16. Su uso actual está muy vinculado a la informática y ciencias de la computación, pues los computadores suelen utilizar el byte u octeto como unidad básica de memoria; y, debido a que un byte representa 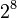 valores posibles, y esto puede representarse como valores posibles, y esto puede representarse como 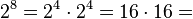  , que equivale al número en base 16 , que equivale al número en base 16 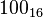 , dos dígitos hexadecimales corresponden exactamente a un byte. , dos dígitos hexadecimales corresponden exactamente a un byte.
En principio, dado que el sistema usual de numeración es de base decimal y, por ello, sólo se dispone de diez dígitos, se adoptó la convención de usar las seis primeras letras del alfabeto latino para suplir los dígitos que nos faltan. El conjunto de símbolos sería, por tanto, el siguiente:

Se debe notar que A = 10, B = 11, C = 12, D = 13, E = 14 y F = 15. En ocasiones se emplean letras minúsculas en lugar de mayúsculas. Como en cualquier sistema de numeración posicional, el valor numérico de cada dígito es alterado dependiendo de su posición en la cadena de dígitos, quedando multiplicado por una cierta potencia de la base del sistema, que en este caso es 16. Por ejemplo: 3E0A16 = 3×163 + E×162 + 0×161 + A×160 = 3×4096 + 14×256 + 0×16 + 10×1 = 15882.
El sistema hexadecimal actual fue introducido en el ámbito de la computación por primera vez por IBM en 1963. Una representación anterior, con 0–9 y u–z, fue usada en 1956 por la computadora Bendix G-15.
|
|
|
|
|
Iniciado por MICROLITO  ..Indigo .. hierro-8-tauro-venus-..mensaje por descifrar'?
-
gabi ..se ve que esperas buenas vibraciones de el msje.).(
ami me parece un msaje productivo aunque pueda ser cataclismico..por la -oposición en las sombras que no pueda ser dominada
-
Edito.:[ quote Indigo]
El sol negro cierra con el solsticio en el heptagrama, digamos que el pentagrama anuncia el nacimiento y el heptagrama la muerte, la hoz de la luna es el codigo de la muerte.
8 - la estrella de las primeras Diosas, encripta el hipercubo en su forma octogonal digamos que en la era dorada, la forma de templo de Salomon, quiere decir cuando llegaron los Dioses -gigantes- Angeles caidos, los cuales regresaran en el proximo ciclo.
Como era simbolo de la Diosa puede ser usado tambien para representar a Venus.
-
prestar atención a ese sim-bolo de la muerte en forma de la hoz de la luna servirá de algo?...por supuesto que las pistas parecen coincidir ,, sólo queda determinar el simbolo de la media luna de la muerte en los -antiguos registros y relacionarlo con las leyendas o realidades sobre catástrofes tipo -sol negro- ,, porque lo que está claro es que el msaje está -escrito" milenios hace y por eso mismo -acertar como los mayas pudieran hacerlo aunque sólo sea en una fracción, es digno de admiración pues en este caso Indigo nos transmite su conocimiento simbólico, siempre contrastable con los datos históricos y de la ´ltima actualidad.S2 de nuevo para indigo..
 |
Click para ampliar |
 Cruz a 60 grados con respecto al norte 90 Cruz a 60 grados con respecto al norte 90
 |
Click para ampliar |
  Puerta de hierro Madrid, refiere a la actual y ultima era de hierro.La forma de la autopista es una version geometrica de la vesica pisicis en forma de lagrima o gota, la misma que vemos bajo la cruz celta del Rey Arturo.En los bordes del cuadro del Rey Arturo esta la S, el cambio de espiral que vemos en la forma del Hospital puerta de hierro.Tambien en el cuadro vemos el sello con el triple espiral del centro de la galaxia.8 el hipercubo, el pulpo, codigo, Octo-pussy de James Bond, pussy refiere tanto al gato como a la vagina y esto una vez que empezamos a desenredar la madeja podemos entender que no es casual.Venus - del Latin Venire - us- nosotros, o sea viene hacia nosotros en su ciclo pentagonal, representa al interaccion pentagonal entre los dos cubos del hipercubo, la estrella de la manzana que es una imagen del microcosmos, nuestros 5 dedos en cada mano son una imagen de esta realidad geometrica, la simetria es producto de la interaccion de los espirales 9 y 6, el ciclope con un ojo es un monstruo singular, hijo de Urano y Gea, Urano es el planeta 7 esta inclinado a 60 grados en su eje, como dicen los textos esotericos es el espejo de la singularidad del centro de la galaxia. Puerta de hierro Madrid, refiere a la actual y ultima era de hierro.La forma de la autopista es una version geometrica de la vesica pisicis en forma de lagrima o gota, la misma que vemos bajo la cruz celta del Rey Arturo.En los bordes del cuadro del Rey Arturo esta la S, el cambio de espiral que vemos en la forma del Hospital puerta de hierro.Tambien en el cuadro vemos el sello con el triple espiral del centro de la galaxia.8 el hipercubo, el pulpo, codigo, Octo-pussy de James Bond, pussy refiere tanto al gato como a la vagina y esto una vez que empezamos a desenredar la madeja podemos entender que no es casual.Venus - del Latin Venire - us- nosotros, o sea viene hacia nosotros en su ciclo pentagonal, representa al interaccion pentagonal entre los dos cubos del hipercubo, la estrella de la manzana que es una imagen del microcosmos, nuestros 5 dedos en cada mano son una imagen de esta realidad geometrica, la simetria es producto de la interaccion de los espirales 9 y 6, el ciclope con un ojo es un monstruo singular, hijo de Urano y Gea, Urano es el planeta 7 esta inclinado a 60 grados en su eje, como dicen los textos esotericos es el espejo de la singularidad del centro de la galaxia. Manos Diosa KaliTigre y elefante007 - Cordenadas del centro de la galaxia - 7 aries al 11 sistema solar.Piña a rombos en la mano simbolo de singularidad por excelencia, en otra mano el cuchillo simil Diosa Kali.Fuego y explosion, el triangulo en dedos abajo, etc. Manos Diosa KaliTigre y elefante007 - Cordenadas del centro de la galaxia - 7 aries al 11 sistema solar.Piña a rombos en la mano simbolo de singularidad por excelencia, en otra mano el cuchillo simil Diosa Kali.Fuego y explosion, el triangulo en dedos abajo, etc.
|
|
|
|
|
PARIS SAMU centro regulador internacional - 15 =1111 Serpiente - Ser-pent -agono - cinco - cinc -fuego
|
|
|
|
|
BARILOCHENSE69-99
69/CANCER
6+9+9+9=33
| milky way in Simple Gematria Equals: 119 |
( |
m 13 |
i9 |
l 12 |
k 11 |
y 25 |
0 |
w 23 |
a1 |
y 25 |
) |
| queen mary in Simple Gematria Equals: 119 |
( |
q 17 |
u 21 |
e5 |
e5 |
n 14 |
0 |
m 13 |
a1 |
r 18 |
y 25 |
|
| hebrew calendar in Simple Gematria Equals: 119 |
( |
h8 |
e5 |
b2 |
r 18 |
e5 |
w 23 |
0 |
c3 |
a1 |
l 12 |
e5 |
n 14 |
d4 |
a1 |
r 18 |
| mary magdalene in Simple Gematria Equals: 119 |
( |
m 13 |
a1 |
r 18 |
y 25 |
0 |
m 13 |
a1 |
g7 |
d4 |
a1 |
l 12 |
e5 |
n 14 |
e5 |
|
| lionsgate in Simple Gematria Equals: 102 |
( |
l
12 |
i
9 |
o
15 |
n
14 |
s
19 |
g
7 |
a
1 |
t
20 |
e
5 |
) |
| lions in Simple Gematria Equals: 69 |
( |
l
12 |
i
9 |
o
15 |
n
14 |
s
19 |
) |
| gate in Simple Gematria Equals: 33 |
( |
g
7 |
a
1 |
t
20 |
e
5 |
) |
|
|
|
|
|
|
7 SEMANAS MAS 62 SEMANAS=69 SEMANAS (SEMANAS/SEMEN/ SEM (LINAJE DE SEM)= PACTO GENESIS 9:11
DANIEL / DAN BROWN / TRANSFIGURACION EN EL MONTE HERMON, EN LA TRIBU DE DAN
EL NUMERO 69, OBVIAMENTE TIENE FUERTE CONNOTACION SEXUAL.
|
|
|
 Primer Primer
 Anterior
57 a 71 de 101
Següent Anterior
57 a 71 de 101
Següent Darrer
Darrer
|

