|
|
General: GEORGES LEMAITRE, UN SACERDOTE CATOLICO, EL PADRE DEL "BIG BANG"
Elegir otro panel de mensajes |
|
|
Georges Lemaître
De Wikipedia, la enciclopedia libre
Georges Henri Joseph Édouard Lemaître (Charleroi, Bélgica, 17 de julio de 1894 – Lovaina, Bélgica, 20 de junio de 1966) fue un sacerdote católico y astrofísico belga.
Georges Lemaître nació el 17 de julio de 1894 en Charleroi, Valonia (Bélgica).Desde muy joven, Lemaître descubrió su doble vocación de religioso y científico. Su padre le aconsejó estudiar primero ingeniería, y así lo hizo, aunque su trayectoria se complicó porque se pasó a la física y además porque, en mitad de sus estudios, estalló la Primera Guerra Mundial. A la edad de 17 años entró en la Escuela de Ingenieros de la Universidad de Lovaina y estudió ingeniería civil. Después de servir como voluntario en el ejército belga durante la Primera Guerra Mundial, empezó a estudiar física y matemáticas, incluyendo la teoría de la relatividad de Albert Einstein. Recibió su doctorado en 1920 y ese mismo año ingresó en el Seminario de Malinas. El 22 de septiembre de 1923 fue ordenado sacerdote por el Cardenal Desiderio José Mercier. Ese año le fueron concedidas dos becas de investigación, una del gobierno belga y otra de una fundación estadounidense, y fue admitido en la Universidad de Cambridge (Inglaterra) como investigador de astronomía.
En junio de 1924 regresó a Bruselas, pero ese mismo año volvió a viajar por motivos científicos, esta vez a Canadá y Estados Unidos. En este último país, además de conocer al astrofísico británico Arthur Stanley Eddington, tuvo la oportunidad de conocer directamente a algunos físicos que, en aquellos momentos, estaban realizando trabajos pioneros en las observaciones astronómicas. Después de un año en la Universidad de Cambridge con Eddington y otro en Cambridge, Massachusetts con Harlow Shapley, regresó a la Universidad de Lovaina como profesor a tiempo parcial. Ahí, en 1927, publicó un informe en el que resolvió las ecuaciones de Einstein sobre la geometría del universo (que Alexander Friedman ya había resuelto, sin que Lemaître lo supiera) y sugirió que se estaba expandiendo, según una de las soluciones, y que es por ello que los astrónomos Vesto Slipher y Carl Wilhelm Wirtz habían observado un corrimiento hacia el rojo de la luz de las nebulosas espirales. En 1931, propuso la idea de que el universo se originó en la explosión de un «átomo primigenio», «huevo cósmico» o hylem. Dicha explosión ahora se llama el Big Bang o Gran Estallido.
La expansión del universo[editar]
Las ecuaciones de la relatividad general, formuladas por Albert Einstein en 1915, permitían estudiar el universo en su conjunto. El mismo Einstein lo hizo, pero se encontró con un universo que cambiaba con el transcurrir del tiempo, y Einstein, por motivos no científicos, prefería un universo inalterable en su conjunto. Para conseguirlo, introdujo en sus ecuaciones un término cuya única función era mantener al universo estable, de acuerdo con sus preferencias personales. Se trataba de una magnitud a la que denominó "constante cosmológica". Años más tarde, Einstein reconoció que había sido el peor error de su trayectoria científica.
Otros físicos también habían desarrollado los estudios del universo tomando como base la relatividad general. Fueron especialmente importantes los trabajos del holandés Willem de Sitter en 1917, y del ruso Aleksandr Fridman en 1922 y 1924. Friedman formuló la hipótesis de un universo en expansión, pero sus trabajos tuvieron escasa repercusión en aquellos momentos.
Lemaître trabajó en esa línea hasta que consiguió una explicación teórica del universo en expansión, y la publicó en un artículo de 1927. Pero, aunque ese artículo era correcto y estaba de acuerdo con los datos obtenidos por los astrofísicos de vanguardia en aquellos años, no tuvo por el momento ningún impacto especial, a pesar de que Lemaître fue a hablar de ese tema, personalmente, con Einstein en 1927 y con Willem de Sitter en 1928 sin conseguir eco en estos científicos.
El 10 de enero de 1930 tuvo lugar en Londres una reunión de la Real Sociedad Astronómica. Al leer el informe que se publicó sobre esa reunión, Georges Lemaître advirtió que tanto De Sitter como Arthur Eddington estaban insatisfechos con el modelo del Universo Estático propuesto por Einstein y buscaban otra solución, que el propio Lemaître ya había hecho pública en 1927, por lo que escribió a Arthur Eddington recordándole ese trabajo de 1927.
Eddington, convencido por lo expuesto por Lemaître dictó el 10 de mayo de 1930 una conferencia ante la Real Sociedad Astronómica sobre ese problema, y en ella informó sobre el trabajo de Lemaître: se refirió a la "contribución decididamente original avanzada por la brillante solución de Lemaître", diciendo que "da una respuesta asombrosamente completa a los diversos problemas que plantean las cosmogonías de Einstein y de De Sitter". El 19 de mayo, De Sitter reconoció también el valor del trabajo de Lemaître, que fue publicado, traducido al inglés, por la Real Sociedad Astronómica.
La fama de Lemaître se consolidó en 1932. Muchos astrónomos y periodistas estaban presentes en Cambridge (Estados Unidos), en la conferencia que Eddington pronunció el día 7 de septiembre en la cual se refirió a la hipótesis de Lemaître como una idea fundamental para comprender el universo. Dos días después en el Observatorio de Harvard, se pidió a Eddington y Lemaître que explicasen su teoría.
El átomo primitivo[editar]
En el artículo titulado "El comienzo del mundo desde el punto de vista de la teoría cuántica" publicado en la revista inglesa Nature, en su edición del día 9 de mayo de 1931,[1] Georges Lemaître sostuvo que si el universo está en expansión, en el pasado, debería haber ocupado un espacio cada vez más pequeño, hasta que, en algún momento original, todo el universo se encontraría concentrado en una especie de "átomo primitivo". Lemaître publicó posteriormente otros artículos sobre el mismo tema, y llegó a publicar un libro titulado "La hipótesis del átomo primitivo". Las ideas expuestas por Lemaître tropezaron no sólo con críticas, sino con una abierta hostilidad por parte de científicos que reaccionaron, a veces, de modo violento. Varios científicos, incluso Albert Einstein, veían con desconfianza la propuesta de Lemaître, que era una hipótesis científica seria, porque, según su opinión, podría favorecer a las ideas religiosas acerca de la creación.
Encuentro con Albert Einstein[editar]
Entre el 24 y el 29 de octubre de 1927 tuvo lugar, en Bruselas, el quinto Congreso Solvay, donde los expositores discutieron acerca de la nueva física cuántica. Georges Lemaître decidió hablar con Einstein sobre su artículo, pero éste le dijo que aunque los cálculos eran correctos, su física era "abominable".[2] Lemaître, convencido de que Einstein se equivocaba esta vez, buscó prolongar la conversación, y también lo consiguió. El profesor Auguste Piccard, que acompañaba a Einstein para mostrarle su laboratorio en la Universidad, invitó a Lemaître a unírseles en el centro educativo. Durante el trayecto, Lemaître aludió a la velocidad de las nebulosas, tema que se encuentra muy relacionado con la expansión del universo. Pero Einstein no parecía estar al corriente de los resultados de las investigaciones al efecto. Piccard, para salvar la situación, comenzó a hablar con Einstein en alemán, idioma que no entendía.
Las relaciones de Lemaître con Einstein mejoraron más tarde. La primera aproximación vino a través de los reyes de Bélgica, que se interesaron por los trabajos de Lemaître y le invitaron a la corte. Einstein pasaba todos los años por Bélgica para visitar a Lorentz y a De Sitter, y en 1929 encontró una invitación de la reina Elisabeth, alemana como Einstein, en la que le pedía que fuera a verla llevando su violín, ya que ejecutaba este instrumento lo mismo que la monarca. Esa invitación fue seguida por muchas otras, de modo que Einstein llegó a ser amigo de los reyes. En una conversación, el rey preguntó a Einstein sobre la famosa teoría de la expansión del universo, e inevitablemente se habló de Lemaître; notando que Einstein se sentía incómodo, la reina le invitó a improvisar, con ella, un dúo de violín.
Otra aproximación se produjo en 1930, en una ceremonia en Cambridge, donde Einstein se encontró con Eddington. De nuevo salió en la conversación la teoría del sacerdote belga, y Eddington la defendió con entusiasmo.
Einstein tuvo varios años para reflexionar antes de encontrarse de nuevo personalmente con Lemaître, en Estados Unidos. Lemaître había sido invitado por el físico Robert Millikan, director del Instituto de Tecnología de California. Entre sus conferencias y seminarios, el 11 de enero de 1933 dirigió un seminario sobre los rayos cósmicos, y Einstein se encontraba entre los asistentes. Esta vez, Einstein se mostró muy afable y felicitó a Lemaître por la calidad de su exposición. Después, ambos se fueron a discutir sus puntos de vista. Einstein ya admitió entonces que el universo está en expansión; sin embargo, no le convencía la teoría del átomo primitivo, que le recordaba demasiado la creación.
En mayo de 1933, Einstein supo que Adolf Hitler había sido nombrado Canciller de la República Alemana, así que renunció a sus cargos en la Academia de Ciencias y en la Universidad de Berlín. En esas circunstancias, Lemaître fue a verle y le organizó varios seminarios. En uno de ellos, Einstein anunció que la conferencia siguiente la daría el propio Lemaître, añadiendo que tenía cosas interesantes que contarles. El sacerdote, en consecuencia, pasó un fin de semana preparando su conferencia, y la dio el 17 de mayo. Einstein le interrumpió varias veces en la conferencia manifestando su entusiasmo, y afirmó entonces que Lemaître era la persona que mejor había comprendido sus teorías de la relatividad.
De enero a junio de 1935, Lemaître estuvo en Estados Unidos como profesor invitado por el Instituto de Estudios Avanzados de Princeton. En Princeton vio por última vez a Einstein. A Einstein le costó aceptar la expansión del universo, aunque finalmente la aceptó, a pesar de que similares motivos le llevaron a rechazar la teoría del átomo primitivo. No obstante que los trabajos de Lemaître fueron cuestionados entre la comunidad científica, debido al hecho de ser también religioso, desde el punto de vista de las ciencias eran serios, y finalmente todos los científicos, Einstein incluido, lo reconocieron y le otorgaron todo tipo de honores.
Lemaître estaba convencido de que ciencia y religión son dos caminos diferentes y complementarios que convergen en la verdad. Al cabo de los años, declaraba en una entrevista concedida al periódico estadounidense The New York Times: "Yo me interesaba por la verdad desde el punto de vista de la salvación y desde el punto de vista de la certeza científica. Me parecía que los dos caminos conducen a la verdad, y decidí seguir ambos. Nada en mi vida profesional, ni en lo que he encontrado en la ciencia y en la religión, me ha inducido jamás a cambiar de opinión".
Al final de su vida se dedicó cada vez más a los cálculos numéricos. Su interés en los computadores y en la informática terminó por fascinarlo completamente. Murió en Lovaina poco después de oír la noticia del descubrimiento de la radiación de fondo de microondas cósmicas, que constituía la prueba de su teoría.
Obras seleccionadas[editar]
- "Un Univers homogène de masse constante et de rayon croissant rendant compte de la vitesse radiale des nébuleuses extragalactiques", Anales de la Sociedad Científica de Bruselas, 47A (1927): 41.
- Nature 128 (1931) suppl.: 704.
- L'hypothèse de l'atome primitif (La hipótesis del átomo primigenio), 1946.
Véase también[editar]
Bibliografía adicional[editar]
Enlaces externos[editar]
HUEVO COSMICO= CONSTELACION DE DELPHINUS = "EXPERIMENTO FILADELFIA"
|
|
|
|
|
 the Apple
| milky way in Simple Gematria Equals: 119 |
( |
m 13 |
i9 |
l 12 |
k 11 |
y 25 |
0 |
w 23 |
a1 |
y 25 |
) |
| queen mary in Simple Gematria Equals: 119 |
( |
q 17 |
u 21 |
e5 |
e5 |
n 14 |
0 |
m 13 |
a1 |
r 18 |
y 25 |
|
| hebrew calendar in Simple Gematria Equals: 119 |
( |
h8 |
e5 |
b2 |
r 18 |
e5 |
w 23 |
0 |
c3 |
a1 |
l 12 |
e5 |
n 14 |
d4 |
a1 |
r 18 |
| mary magdalene in Simple Gematria Equals: 119 |
( |
m 13 |
a1 |
r 18 |
y 25 |
0 |
m 13 |
a1 |
g7 |
d4 |
a1 |
l 12 |
e5 |
n 14 |
e5 |
|
|
|
|
|
|
16. Génesis 49:27 Benjamín es lobo arrebatador; A la mañana comerá la presa, Y a la tarde repartirá los despojos.
169. Romanos 11:1 Digo, pues: ¿Ha desechado Dios a su pueblo? En ninguna manera. Porque también yo soy israelita, de la descendencia de Abraham, de la tribu de Benjamín. 170. Filipenses 3:5 circuncidado al octavo día, del linaje de Israel, de la tribu de Benjamín, hebreo de hebreos; en cuanto a la ley, fariseo;
PABLO, ESTA EN FUNCION A LA MISMA SANTA CENA, OSEA EL MISMO RELOJ.
JERUSALEN ESTABA EN LA TRIBU DE BENJAMIN, OSEA QUE ES OBVIO QUE LA NUEVA JERUSALEN ES PABLO MISMO
PABLO/PEQUEÑO/PERRO/LOBO/GUERRA/MARTE/GRIAL
PABLO ES UN TIPO DEL GRIAL MISMO
16. Génesis 49:27 Benjamín es lobo arrebatador; A la mañana comerá la presa, Y a la tarde repartirá los despojos.
169. Romanos 11:1 Digo, pues: ¿Ha desechado Dios a su pueblo? En ninguna manera. Porque también yo soy israelita, de la descendencia de Abraham, de la tribu de Benjamín. 170. Filipenses 3:5 circuncidado al octavo día, del linaje de Israel, de la tribu de Benjamín, hebreo de hebreos; en cuanto a la ley, fariseo;
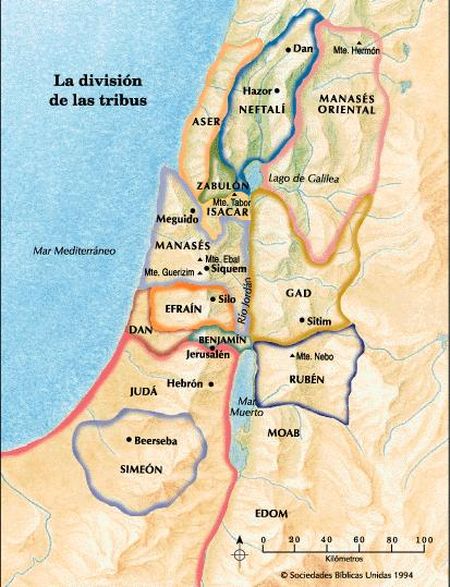 LAS DOCE TRIBUS DE ISRAEL
13 HIJOS MAS DINA, LA UNICA HIJA MUJER
JABOB=ISRAEL=VENCEDOR
The classic logarithmic Golden Spiral
LLAVE DE ORO Y DE PLATA AL IGUAL QUE LA MANZANA
| milky way in Simple Gematria Equals: 119 |
( |
m 13 |
i9 |
l 12 |
k 11 |
y 25 |
0 |
w 23 |
a1 |
y 25 |
) |
| queen mary in Simple Gematria Equals: 119 |
( |
q 17 |
u 21 |
e5 |
e5 |
n 14 |
0 |
m 13 |
a1 |
r 18 |
y 25 |
|
| hebrew calendar in Simple Gematria Equals: 119 |
( |
h8 |
e5 |
b2 |
r 18 |
e5 |
w 23 |
0 |
c3 |
a1 |
l 12 |
e5 |
n 14 |
d4 |
a1 |
r 18 |
| mary magdalene in Simple Gematria Equals: 119 |
( |
m 13 |
a1 |
r 18 |
y 25 |
0 |
m 13 |
a1 |
g7 |
d4 |
a1 |
l 12 |
e5 |
n 14 |
e5 |
|
| milky way in Simple Gematria Equals: 119 |
( |
m 13 |
i9 |
l 12 |
k 11 |
y 25 |
0 |
w 23 |
a1 |
y 25 |
) |
| queen mary in Simple Gematria Equals: 119 |
( |
q 17 |
u 21 |
e5 |
e5 |
n 14 |
0 |
m 13 |
a1 |
r 18 |
y 25 |
|
| hebrew calendar in Simple Gematria Equals: 119 |
( |
h8 |
e5 |
b2 |
r 18 |
e5 |
w 23 |
0 |
c3 |
a1 |
l 12 |
e5 |
n 14 |
d4 |
a1 |
r 18 |
| mary magdalene in Simple Gematria Equals: 119 |
( |
m 13 |
a1 |
r 18 |
y 25 |
0 |
m 13 |
a1 |
g7 |
d4 |
a1 |
l 12 |
e5 |
n 14 |
e5 |
|
|
|
|
|
|
Hércules (constelación)
De Wikipedia, la enciclopedia libre
Recibe su nombre del héroe mitológico, Hércules y es la quinta en tamaño de las 88 constelaciones modernas. También era una de las 48 constelaciones de Ptolomeo.
[editar] Características destacables
No tiene estrellas de primera magnitud, siendo la más brillante β Herculis con magnitud 2,78. μ Herculis se encuentra a 27,4 años luz de la Tierra. El Ápex solar (punto del cielo que indica la dirección hacia la que se mueve el Sol en su órbitaalrededor del centro de la galaxia) se encuentra en Hércules, cerca de ξ Herculis.
[editar] Estrellas principales
- α Herculis (Ras Algethi o Rasalgethi), de magnitud 3,31, es un sistema estelar triple, cuya estrella principal es una gigante roja variable.
- β Herculis (Kornephoros), la más brillante de la constelación con magnitud 2,78, una estrella gigante amarilla.
- γ Herculis, gigante blanca de magnitud 3,74. Es una binaria espectroscópica con un período orbital de 11,9 días.
- δ Herculis (Sarin), estrella blanca de magnitud 3,12; es una estrella binaria cuyas componentes han sido resueltas por interferometría.
- ε Herculis, binaria espectroscópica de magnitud 3,91.
- ζ Herculis, la segunda más brillante de la constelación con magnitud 2,89, estrella doble formada por dos estrellas amarillas de desigual brillo.
- η Herculis, gigante amarilla de magnitud 3,49.
- θ Herculis, gigante luminosa naranja de magnitud 3,85.
- ι Herculis, subgigante azul de magnitud 3,79; tres estrellas más completan este sistema estelar cuádruple.
- κ Herculis A y κ Herculis B, dos gigantes que forman una doble óptica.
- λ Herculis (Maasym), gigante naranja de magnitud 4,40.
- μ Herculis, sistema estelar cercano que dista del Sistema Solar 27,4 años luz.
- π Herculis, gigante naranja de magnitud 3,16.
- ρ Herculis, estrella doble cuyas componentes, separadas 4 segundos de arco, brillan con magnitud 4,56 y 5,42.
- τ Herculis, estrella B pulsante lenta (SPB) con una tenue compañera a 7,6 segundos de arco.
- χ Herculis, enana amarilla de baja metalicidad que se encuentra a 52 años luz de distancia.
- ω Herculis (Kajam), de magnitud 4,57.
- 8 Herculis, estrella blanca de magnitud 6,13 que forma una doble óptica con Kappa Herculis —separación 0,2º—.
- 14 Herculis, enana naranja a 59,2 años luz con una enana marrón o planeta gigante alrededor. En 2006 se descubrió un posible segundo compañero, aún sin confirmar.
- 30 Herculis (g Herculis), gigante roja y variable semirregular cuyo brillo oscila entre magnitud 4,3 y 6,3 en un ciclo de 89,2 días.
- 68 Herculis (u Herculis), binaria eclipsante en donde existe transferencia de masa desde la secundaria hacia la primaria.
- 72 Herculis (w Herculis), enana amarilla similar al Sol a 47 años luz de distancia.
- 89 Herculis, supergigante amarilla en las etapas finales de su evolución estelar.
- 95 Herculis, estrella binaria compuesta por una gigante blanca y una gigante amarilla separadas 6,3 segundos de arco.
- 99 Herculis, binaria de baja metalicidad cuya primaria es una enana amarilla de magnitud 5,20.
- 101 Herculis, gigante blanca de magnitud 5,11.
- 109 Herculis, gigante naranja de magnitud 3,84, la duodécima estrella más brillante de la constelación.
- 111 Herculis, estrella blanca de magnitud 4,35.
- X Herculis, variable pulsante semirregular cuyo brillo varía entre magnitud 6 y 7 en un período de 95 días.
- SZ Herculis y FN Herculis, binarias eclipsantes de magnitud 9,94 y 11,08 respectivamente.
- UX Herculis, binaria eclipsante de magnitud 9,05; durante el eclipse principal su brillo disminuye 1,16 magnitudes.
- OP Herculis, gigante luminosa roja variable entre magnitud 5,85 y 6,73.
- HD 147506, subgigante amarilla en donde se ha detectado un planeta masivo (HAT-P-2b) en una órbita excéntricacercana a la estrella.
- HD 149026, estrella subgigante con un planeta cuya masa es similar a la de Saturno.
- HD 154345, enana amarilla a 58,91 años luz con un planeta extrasolar.
- Gliese 623, estrella binaria compuesta por dos enanas rojas.
- Gliese 686 y Gliese 649, enanas rojas a 26,5 y 33,7 años luz respectivamente; la segunda de ellas posee un planeta.
- HD 155358, estrella de baja metalicidad con dos planetas que interactúan gravitacionalmente.
- Gliese 638 y HR 6806, enanas naranjas situadas respectivamente a 31,9 y 36,2 años luz de distancia de la Tierra.
- GD 362, enana blanca con un anillo similar a los de Saturno.
- http://es.wikipedia.org/wiki/H%C3%A9rcules_(constelaci%C3%B3n)
  
ISLA SAN GIORGIO (VENECIA)=GEORGE LEMAITRE
GEMATRIA EN INGLES DE SEED=33
GEMATRIA EN INGLES DE GATE=33
SARA (CE-SAREA DE FILIPO)=PARALELO 33
"¡Oh profundidad de las riquezas de la sabiduría (sophia)
y de la ciencia (gnwsiV, gnosis) de Dios!
¡Cuán incomprensibles son sus juicios, e inescrutables sus caminos!"
(Romanos, 11: 33).
25 DE ABRIL=DIA DE SAN MARCOS
22 DE JULIO=DIA DE MARIA LA MAGDALENA
|
|
|
|
|
 
|
4. SCALA CONTARINI DEL BOVOLO: 45.434838, 12.334694
Ya aviso que no es nada fácil de encontrar, de hecho, es uno de esos rincones que pasan totalmente desapercibidos a menos que sepas de su existencia. Normalmente, todos los palacios tienen dos entradas, una principal que da hacia el Gran Canal y que es más espectacular, y otra secundaria que era usada por el servicio. Pues bien, este es de los pocos palacios en los que su entrada secundaria es casi más bonita que la principal, todo gracias a una maravillosa escalera de Caracol que hace las delicias de los descubridores viandantes (Bovolo significa Caracol).
Cerca de este Palacio se encuentra el famoso teatro de La Fenice, donde han sonado las Óperas italianas más importantes de la historia.
|
|
|
|
|
|
SCALA CONTARINI DEL BOVOLO
Escondida en un laberinto de calles y canales, a pocos pasos de Campo Manin, en uno de los principales itinerarios turísticos venecianos, surge una joya arquitectónica caracterizada de un estilo entre renacimental (por la utilización de algunos elementos), gótica (por la técnica de costrucción) y veneto-bizantina (por la forma): la Scala Contarini del Bovolo.
La escalera a espiral más importante y prestigiosa de Venecia, fue encargada su realización por Pietro Contarini a finales del 1400, con el objetivo de decorar la fachada del colindante Palazzo San Paternian de propiedad de la ilustre familia veneciana.
La realización de esta ópera, no tenía al inicio un verdadero motivo funcional, consistía simplemente en un acto de prestigio, se buscaba únicamente aumentar la popularidad y prestigio del clan familiar.
La creación de la escalera ha tenido una resonancia tan fuerte que llevó a la ciudadanía a dar un nombre característico a la familia, como “Contarini del Bovolo” (por la forma particular de la escalera a forma de caparazón de caracol, que en veneciano se dice “bovolo”).
El pórtico en el segundo piso de la Scala del Bovolo conduce a una sala prestigiosa del Palazzo Contarini (Sala del Tintoretto) en donde se encuentran expuestas las obras provenientes de la colección de arte del IRE, que está constituída de pinturas, esculturas y objetos de un significado importante de época veneciana con los más ilustres protagonistas del panorama artístico veneciano del 1500 al 1700.
Cerrado:
1 de Enero, 15 agosto, 1 noviembre, 25 y 26 diciembre.
Cierre extraordinario: 9 abril de las 10:00 a las 12,30
La ventanilla cierra 30 minutos antes de que cierre el museo.
Precios
- 7€ Entero
- 6€ Reducido: Menores de 26 años, Mayores de 65, Socios FAI
Gratuito:
- Menores hasta12 años
- Guías Turísticas autorizadas
- Residentes en Venecia (con documento de reconocimiento y residencia)
- Dependientes IRE y Fundación Venecia Servicios a la Persona
Las entradas gratuitas deben ser adquiridas en la ventanilla. No se pueden reservar. Reservación obligatoria para grupos de más de 10 personas.
https://www.todayinvenice.com/es/exposiciones-y-museos/museos/scala-contarini-del-bovolo/502/2018-06-27 |
|
|
|
|
|
|
|
1. Génesis 28:12 Y soñó: y he aquí una ESCALERA que estaba apoyada en tierra, y su extremo tocaba en el cielo; y he aquí ángeles de Dios que subían y descendían por ella.
2. 1 Reyes 6:8 La puerta del aposento de en medio estaba al lado derecho de la casa; y se subía por una ESCALERA de caracol al de en medio, y del aposento de en medio al tercero.
3. Ezequiel 41:7 Y había mayor anchura en las cámaras de más arriba; la ESCALERA de caracol de la casa subía muy alto alrededor por dentro de la casa; por tanto, la casa tenía más anchura arriba. Del piso inferior se podía subir al de en medio, y de éste al superior.
| Reply |
Message 89 of 90 on the subject |
|
|
|
|
| Reply |
Message 90 of 90 on the subject |
|
|
|
|
|
|
|
|
|
|
|
 
|
LLAVE DE ORO Y DE PLATA AL IGUAL QUE LA MANZANA
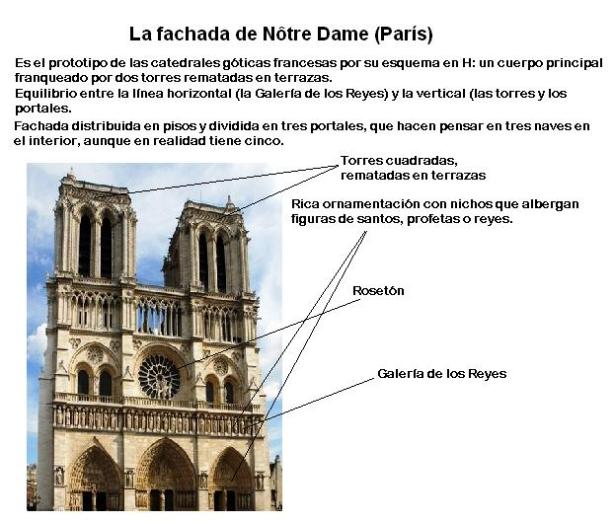
Incendio Notre Dame: Última hora de la catedral de París (15 DE ABRIL)
 Incendio Notre Dame (París), en directo (Bertrand Guay / AFP)
PHI A NOTRE-DAME
A la catredal de Notre Dame hi observem més rectanlges auris: Creat per Mario Pastor 
The DaVinci Code, Notre Dame Cathedral from DaVinci Code
original movie prop
HEXAGONO=OCTAHEDRO =ESTRELLA DE 6 PUNTAS= SATURNO =CUBO/HEXAGONO= ESPACIO/TIEMPO =1 DE REYES 6:20 Y APOCALIPSIS 21:16
EL SEXTO DIA ES EL VIERNES Y EL OCTAVO EL DOMINGO. INCREIBLE
   
August 23, 2018/
The Golden Section (aka Golden Mean, and Golden Ratio) phys.org
We use math in architecture on a daily basis to solve problems. We use it to achieve both functional and aesthetic advantages. By applying math to our architectural designs through the use of the Golden Section and other mathematical principles, we can achieve harmony and balance. As you will see from some of the examples below, the application of mathematical principles can result in beautiful and long-lasting architecture which has passed the test of time.
Using Math in Architecture for Function and Form
We use math in architecture every day at our office. For example, we use math to calculate the area of a building site or office space. Math helps us to determine the volume of gravel or soil that is needed to fill a hole. We rely on math when designing safe building structures and bridges by calculating loads and spans. Math also helps us to determine the best material to use for a structure, such as wood, concrete, or steel.
“Without mathematics there is no art.” – Luca Pacioli, De divina proportione, 1509
Architects also use math when making aesthetic decisions. For instance, we use numbers to achieve attractive proportion and harmony. This may seem counter-intuitive, but architects routinely apply a combination of math, science, and art to create attractive and functional structures. One example of this is when we use math to achieve harmony and proportion by applying a well-known principle called the Golden Section
Math and Proportion – The Golden Section
Perfect proportions of the human body – The Vitruvian Man – by Leonardo da Vinci.
We tend to think of beauty as purely subjective, but that is not necessarily the case. There is a relationship between math and beauty. By applying math to our architectural designs through the use of the Golden Section and other mathematical principles, we can achieve harmony and balance.
The Golden Section is one example of a mathematical principle that is believed to result in pleasing proportions. It was mentioned in the works of the Greek mathematician Euclid, the father of geometry. Since the 4th century, artists and architects have applied the Golden Section to their work.
The Golden Section is a rectangular form that, when cut in half or doubled, results in the same proportion as the original form. The proportions are 1: the square root of 2 (1.414) It is one of many mathematical principles that architects use to bring beautiful proportion to their designs.
Examples of the Golden Section are found extensively in nature, including the human body. The influential author Vitruvius asserted that the best designs are based on the perfect proportions of the human body.
Over the years many well-known artists and architects, such as Leonardo da Vinci and Michelangelo, used the Golden Section to define the dimensions and proportions in their works. For example, you can see the Golden Section demonstrated in DaVinci’s painting Mona Lisa and his drawing Vitruvian Man.
Famous Buildings Influenced by Mathematical Principles
Here are some examples of famous buildings universally recognized for their beauty. We believe their architects used math and the principals of the Golden Section in their design:
Parthenon
The classical Doric columned Parthenon was built on the Acropolis between 447 and 432 BC. It was designed by the architects Iktinos and Kallikrates. The temple had two rooms to shelter a gold and ivory statue of the goddess Athena and her treasure. Visitors to the Parthenon viewed the statue and temple from the outside. The refined exterior is recognized for its proportional harmony which has influenced generations of designers. The pediment and frieze were decorated with sculpted scenes of Athena, the Gods, and heroes.
Parthenon Golden Section
Notre Dame Cathedral in Paris
Built on the Ile de la Cite, Notre Dame was built on the site of two earlier churches. The foundation stone was laid by Pope Alexander III in 1163. The stone building demonstrates various styles of architecture, due to the fact that construction occurred for over 300 years. It is predominantly French Gothic, but also has elements of Renaissance and Naturalism. The cathedral interior is 427 feet x 157 feet in plan. The two Gothic towers on the west façade are 223 feet high. They were intended to be crowned by spires, but the spires were never built. The cathedral is especially loved for its three stained glass rose windows and daring flying buttresses. During the Revolution, the building was extensively damaged and was saved from demolition by the emperor Napoleon.
Notre Dame Cathedral in Paris
Taj Mahal
Built in Agra between 1631 and 1648, the Taj Mahal is a white marble mausoleum designed by Ustad-Ahmad Lahori. This jewel of Indian architecture was built by Emperor Shah Jahan in memory of his favorite wife. Additional buildings and elements were completed in 1653. The square tomb is raised and is dramatically located at the end of a formal garden. On the interior, the tomb chamber is octagonal and is surrounded by hallways and four corner rooms. Building materials are brick and lime veneered with marble and sandstone.
Taj Mahal designed by Ustad-Ahmad Lahori
As you can see from the above examples, the application of mathematical principles can result in some pretty amazing architecture. The architects’ work reflects eye-catching harmony and balance. Although these buildings are all quite old, their designs have pleasing proportions which have truly passed the test of time.
https://bleckarchitects.com/math-in-architecture/
|
|
|
|
|
|
|
 St. George Tabernacle Clock - St. George, Utah Posted by:  BruceS
N 37° 06.469 W 113° 35.095
12S E 270308 N 4109960
Quick Description: Clock for the historic tabernacle in St. George, Utah.
Location: Utah, United States
Date Posted: 11/4/2008 6:44:44 AM
Waymark Code: WM53BM
|
|
|
|
|
LA BIBLIA SE ESTUDIA TEXTO Y CONTEXTO O EL MARCO DEL TEXTO. POR ESO LA MAYORIA DE LAS DENOMINACIONES CAEN EN LA MENTIRA DE LA CREENCIA DE QUE CRISTO ES UN DIOS TODOPODEROSO, PORQUE DESGRACIADAMENTE SE BASAN EN UNOS POCOS VERSICULOS NEGANDO EL MARCO DE LA BIBLIA. SI SE ESTUDIARA EL MARCO, OBVIAMENTE EL MUNDO ENTENDERIA DE QUE CRISTO FUE UN HOMBRE 100%, QUE NO TUVO PREEXISTENCIA, CASADO CON UNA MUJER Y OBVIAMENTE CON UN HIJO. EL DRAMA DE BABILONIA ES QUE NO ESTUDIA EL MARCO.
1 Pedro 5:13: La iglesia que está en Babilonia, elegida juntamente con vosotros, y Marcos mi HIJO, os saludan.
|
|
|
|
|
El síndrome de Estocolmo cierra la trama del Tráiler final «The Big Bang Theory»
Este 16 de mayo llegará a su final The Big Bang Theory» luego de 12 temporadas, con el cambio constante y el síndrome de Estocolmo cierra la trama del Tráiler final. Cabe señalar que el desenlace de «The Big Bang Theory» se terminó de grabar el pasado 30 de abril.
La comedia de la CBS Broadcasting Inc, cadena de televisión comercial en Estados Unidos, emitirá su desenlace en dos capítulos: El cambio constante y El síndrome de Estocolmo, ambos prometen despertar la nostalgia y cerrar con broche de oro sus apariciones en pantalla chica.
El tráiler oficial del gran final se trata de un recuento sobre la historia de los personajes, su evolución y el afecto suscitado a raiz de las relaciones de afecto por la convivencia con Sheldon Cooper, el misántropo protagonista de la historia de 12 temporadas.
Entre los ejemplos más evidente en está trama final es como Leonard (Johnny Galecki) buscará convertirse en el investigador principal de un estudio de física de plasmas, cambio radical parte de un estado de cambio constante en los roles de los personajes.
https://www.vivanicaragua.com.ni/2019/05/11/variedades/el-sindrome-de-estocolmo-cierra-la-trama-del-trailer-final-the-big-bang-theory/ |
|
|
 Primer
Anterior
49 a 63 de 78
Siguiente
Último
|
|
| |
|
|
©2024 - Gabitos - Todos los derechos reservados | |
|
|
La escalera de Bramante, en los Museos Vaticanos
